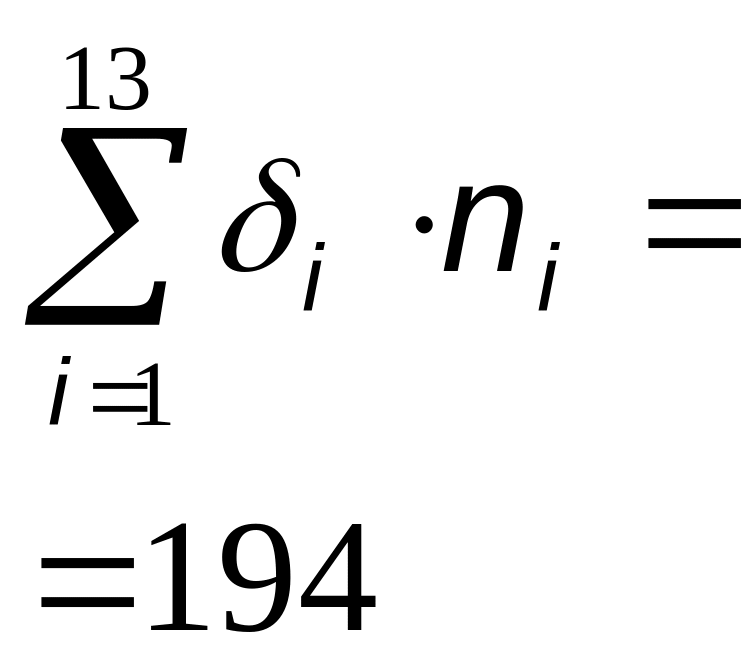1 Статистический анализ искажений
Сигналы, передаваемые в канал связи, подвержены влиянию различного рода помех, в результате чего значение искажений изменяются случайным образом. Это дает основание все вопросы, связанные с характером изменения искажений рассматривать с вероятностной точки зрения.
Приемные оконечные устройства обладают определенной защищенностью от искажений, то есть исправляющей способностью. При превышении величины искажений исправляющей способности возникнет ошибка. Для оценки использования оконечных устройств и канала связи в системе передачи дискретной информации проводят анализ краевых искажений статистическим методом. Для этого проводят измерения искажений, составляют таблицу наблюдений, строят гистограмму, отображающую ряд распределений искажений. Результаты измерений в виде интервалов смещений и повторяемости представлены заданием и приводятся в табл. 1.
Графической интерпретацией приведенной таблицы может служить гистограмма наблюдений, то есть график, построенный из прямоугольников, по оси абсцисс которых отложены интервалы смещений, а отметки на оси ординат пропорциональны повторяемости смещений. По к ширине интервала i – значения нормированной частоты, рассчитываемой по формуле:
![]() , (1.1)
, (1.1)
где ni – повторяемость смещений;
i – интервал смещений.
Гистограмма дает наглядное представление о характере распределения смещений. Однако для расчетов желательно аппроксимировать ее непрерывной функцией, которая как можно точнее соответствовала бы результатам измерений. Форма гистограммы, представленной на рисунке 1, и физическая сущность краевых искажений позволяет предположить, что последняя может быть достаточно точно аппроксимирована функцией нормального закона распределения. Плотность вероятностей нормального закона распределения определяется соотношением:
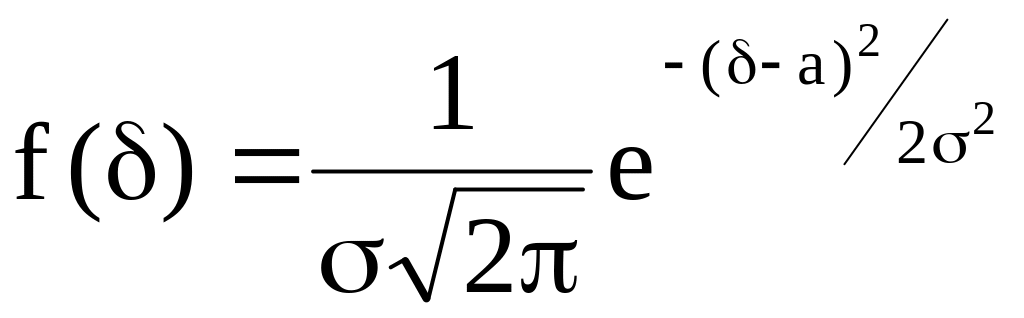 , (1.2)
, (1.2)
где – случайная величина, в данном случае относительное значение краевого искажения;
– математическое ожидание случайной величины;
– среднее квадратическое отклонение от значения ;
Нормальный закон полностью определяется параметрами и :
 (1.3)
(1.3)  (1.4)
(1.4)
Данные для расчета параметров нормального закона распределения и построения кривой f() приведены в табл. 1. По данным этой таблицы в соответствии (1.3) и (1.4) находим: = 0,18216 %; = 4,233955 %.
Кривая нормального закона распределения изображена на рис.1.
Таблица №1.
Интервалы смещений i, % |
Повторяе- мость сме- щений ni |
Значение случайной величины i, % |
iּni |
(i–a)2ּni |
Норми- рованная частота
|
Ординаты кривой f() |
–50 –11 |
2 |
–30,5 |
-61 |
1882.7898 |
0.000048 |
0 |
–11 –9 |
7 |
–10 |
-70 |
725.73462 |
0.003286 |
0.005227685 |
–9 –7 |
23 |
–8 |
-184 |
1539.7979 |
0.010798 |
0.014561759 |
–7 –5 |
67 |
–6 |
-402 |
2560.6795 |
0.031455 |
0.032449797 |
–5 –3 |
117 |
–4 |
-468 |
2046.3837 |
0.054930 |
0.057850067 |
–3 –1 |
185 |
–2 |
-370 |
880.93682 |
0.086854 |
0.082506748 |
–1 1 |
212 |
0 |
0 |
7.0346113 |
0.099531 |
0.094138833 |
1 3 |
208 |
2 |
416 |
687.34508 |
0.097653 |
0.08592942 |
3 5 |
137 |
4 |
548 |
1996.899 |
0.064319 |
0.062749271 |
5 7 |
67 |
6 |
402 |
2267.7669 |
0.031455 |
0.036658038 |
7 9 |
29 |
8 |
232 |
1772.4402 |
0.013615 |
0.017132608 |
9 11 |
9 |
10 |
90 |
867.50991 |
0.004225 |
0.006405772 |
11 50 |
2 |
30,5 |
61 |
1838.3429 |
0.000048 |
0 |
|
|
|
|
|||
 ;
;

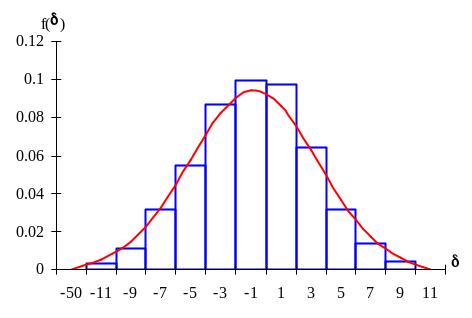
Рис. 1. Гистограмма и кривая нормального закона распределения.