4. Определение параметров функциональной зависимости

методом наименьших квадратов

При совместном исследовании двух случайных величин по имеющейся выборке (х₁, у₂), (х₂, у₂),…,(x_k, y_k) возникает задача определения зависимости между ними. Если вид функции y = f (x, a, b,...) задан, то требуется найти значения коэффициентов a, b,..., при которых y_i наименее отличаются от f (x_i). В методе наименьших квадратов коэффициенты должны быть такими, что принимает минимальное значение.

а) Линейная зависимость y = ax + b. Если , то из условия получаем:

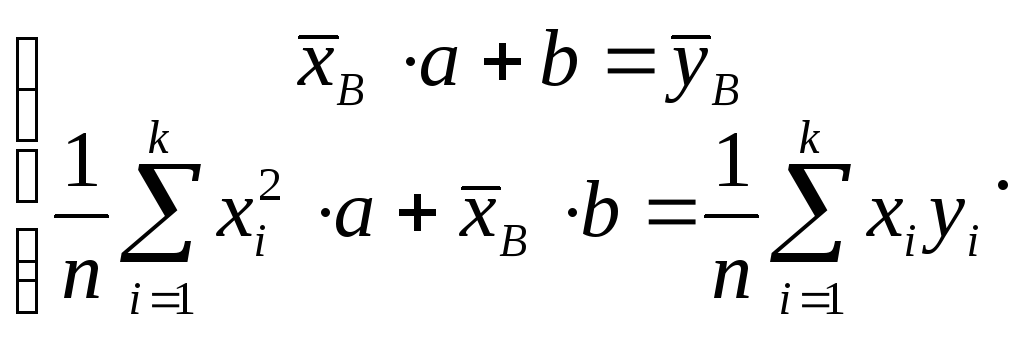
б) Квадратичная зависимость y = (ax + b)². Отсюда и система для определения a, b может быть получена по аналогии с предыдущим случаем с помощью замены y_i на :

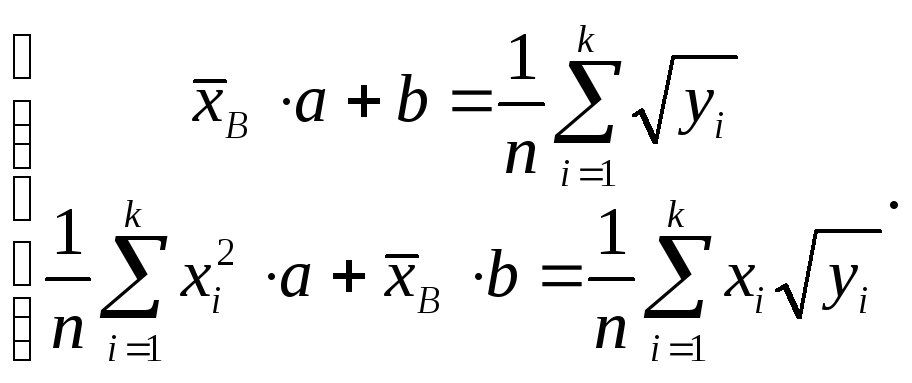
в) Показательная зависимостьЛогарифмируя, получаем: lny=ax + b, и система уравнений для a, b имеет вид:

г) Зависимость вида Тогда y² = ax + b, и условия для а и b можно задать так:

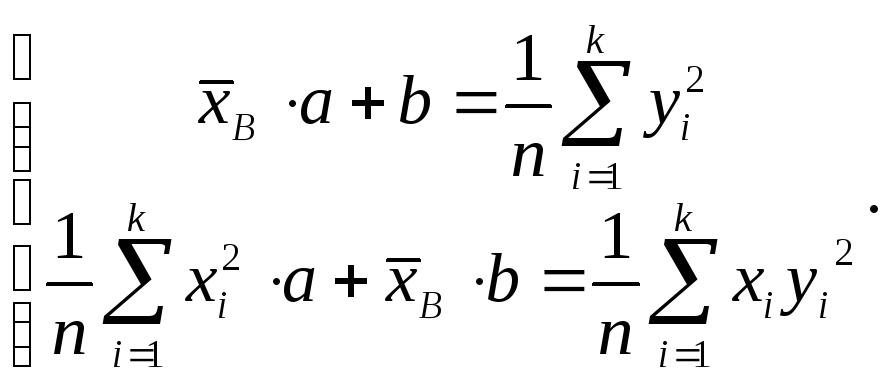
д) Логарифмическая зависимость y = ln(ax + b), то есть e^y = ax + b, и

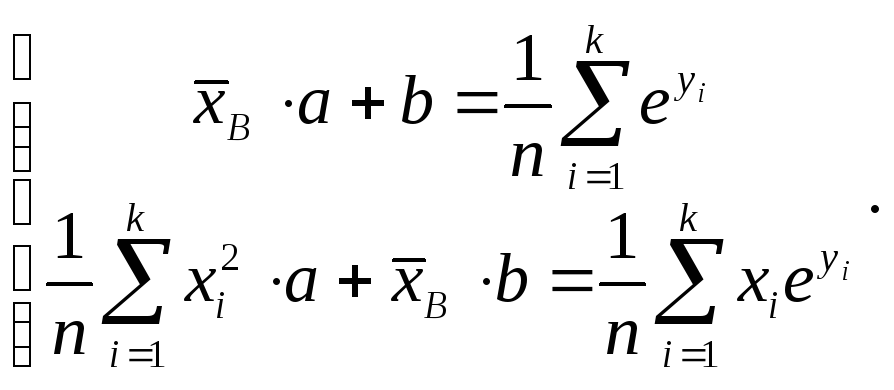
Пример 5. Найти параметры зависимости между х и у для выборки

xi	1,4	1,7	2,6	3,1	4,5	5,3
yi	2,5	4,7	18,3	29,8	74,2	110,4

для случаев: 1) линейной зависимости y = ax + b;

2) квадратичной зависимости y = (ax + b)²;

3) показательной зависимости y = e^{ax + b}.

Определить, какая из функций является лучшим приближением зависимости между х и у.

Решение.

По виду выборки достаточно очевидно, что связь между х и у скорее всего не является линейной – у растет не пропорционально х. Проверим это предположение, найдя коэффициенты а и b для каждой из функций. Для этого вычислим предварительно = 3,1; = 40,0;

Теперь можно решать линейные системы для а и b:

1) то есть линейная зависи-мость имеет вид: у = 27,34х – 44,74.

2) квадратичная функция:

у = (2,29х – 1,68)².

3) показательная функция:

у = е^{0,94х + 0,04}.

Вычислим значения

:

yi	2,5	4,7	18,3	29,8	74,2	110,4
(yi)лин	-6,46	1,74	26,34	40,0	78,29	100,13	379,93
(yi)кв	2,33	4,9	18,27	29,37	74,4	109,35	1,397
(yi)показ	3,85	5,09	11,67	18,8	69,5	146,66	1503,81

Итак, наилучшим приближением является квадратичная функция.

II. Элементы теории корреляции