
Теория поля
.pdf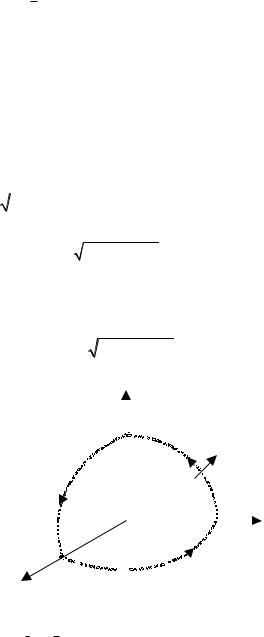
Ц = !ò (a,τ 0 )dl = òò(rota,n0 )ds;
LS
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
rot a = |
¶ |
|
|
|
|
|
|
¶ |
|
|
|
|
|
|
|
¶ |
|
|
= -2(x + y) |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
¶x |
|
|
|
¶y |
|
|
|
|
¶z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
y2 |
|
-x2 |
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
n0 = |
|
grad F |
|
|
|
, F (x, y, z) = x2 + z2 -1+ y; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
grad F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
n0 = |
2 |
xi |
|
j |
+ 2zk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4x2 +1+ 4z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1−x2 |
|||
Ц = òò-2(x + y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds = -2òò(x + y)dxdy = -2òdx ò (x + y)dy = |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
4x |
2 |
+1+ 4z |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ xy |
|
|
|
|
|
|
0 |
|
0 |
|||||||||||||||||||||||
|
1 æ |
|
|
|
|
|
|
|
|
|
|
y2 ö |
|
1−x2 |
|
|
|
|
1 |
é |
|
|
|
|
|
|
|
2 |
|
1 |
|
|
2 |
|
2 ù |
|
|
|
7 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
= -2òç xy + |
|
|
÷ |
|
0 |
|
|
|
|
|
|
dx |
= -2ò |
êx(1 |
- x |
|
)+ |
|
(1- x |
|
) |
ú dx = - |
|
|
|
; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
0 è |
|
|
|
|
|
|
|
|
|
|
2 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
ë |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
û |
|
10 |
|
||||||||||||
ds = |
|
dxdy |
|
;cosγ = |
|
|
|
|
|
|
|
|
2z |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
cosγ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4x2 +1+ 4z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ xy |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x
Задача3. Вычислитьциркуляциювекторногополя a(M ) = xj - zk
вдольконтура,полученногоприпересеченииконуса x2 + y2 = (z - 3)2
скоординатнымиплоскостями(см.рис.5.4) a) непосредственно,б)потеоремеСтокса..
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com
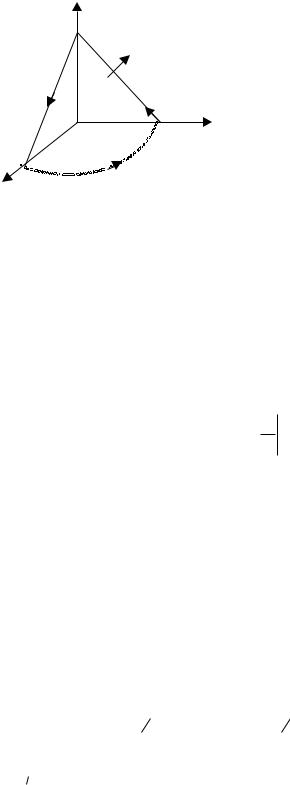
z
3C
n 0
Рис.5.4.
B
0 |
y |
3
A
3
x
Решение.а)Линия L состоитиздвухотрезков BC и CA
1) |
Наотрезке BC имеем |
|
|
|
|
|
|
|
|
x = 0,dx = 0; |
|
|
|
|
|
|
|
||
y = 3- z;dy = -dz (0 £ z £ 3) |
|
|
|
|
|
|
|
||
|
|
3 |
z |
2 |
|
|
3 |
9 |
|
|
|
|
|||||||
ò Pdx + Qdy + Rdz = ò -zdz = -ò zdz = - |
|
|
|
= - |
|||||
2 |
2 |
||||||||
BC |
BC |
0 |
|
|
0 |
||||
|
|
|
|
||||||
2) Наотрезке CA имеем
y= 0,dy = 0;
x = 3- z;dx = -dz,
òPdx + Qdy + Rdz = ò xdy - zdz = - ò zdz = -ò0 zdz
CA |
|
|
|
CA |
CA |
3 |
3) Надуге |
|
|
|
|||
AB имеем |
|
|
||||
ì |
2 |
+ y |
2 |
= 9, |
|
|
íx |
|
|
|
|
||
îz = 0 |
|
|
|
|
||
дуги AB окружности.
.
= - z2 0 = 9 . 2 3 2
параметрическиеуравнениядуги
ìx = 3cost, |
|
π |
|
ï |
£ t £ |
, |
|
íy = 3sin t,0 |
2 |
||
ï |
|
|
|
îz = 0, |
|
|
|
поэтому
dx = −3sin tdt, dy = 3costdt, dz = 0,
ò Pdx + Qdy + Rdz = ò xdy -
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
AB |
|
= |
9 |
æ |
- |
sin 2t ö |
|
π 2 |
= |
9 |
π. |
|
|
||||||||||
2 |
ç1 |
2 |
÷ |
|
|
4 |
||||
|
è |
|
ø |
|
0 |
|
|
|||
|
|
|
|
|
||||||
AB имеютвид
1 |
9 |
1 |
zdz = ò2 (3cos t ×3cost)dt = |
ò2 (1- cos 2t)dt = |
|
0 |
2 |
0 |
витогеполучаем |
9 |
|
9 |
|
9 |
|
9 |
|
|
Ц = ò+ ò+ ò= - |
+ |
+ |
π = |
π. |
|||||
2 |
2 |
4 |
4 |
||||||
BC CA AB |
|
|
|
|
б)ВычисляемциркуляциюпотеоремеСтокса.Находим
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com

|
|
|
|
|
|
|
|
i |
|
|
|
|
|
j |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rot a = |
|
¶ |
|
|
¶ |
|
|
¶ |
|
|
= 0× |
|
|
|
+ 0× |
|
|
+ |
|
|
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
i |
|
j |
k |
k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
¶x |
|
|
¶y |
¶z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
x |
-z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Вкачествеповерхности S выбираемконус |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
x2 + y2 = (z - 3)2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Тогда(см.рис.5.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
n |
0 |
= |
xi |
+ yj |
- (z - 3)k |
|
= |
|
xi |
+ yj |
- (z - 3)k |
, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x2 + y2 + (z - 3)3 |
|
|
|
|
2(x2 + y2 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Ц = òò(rot a,n0 )ds = 9òò |
|
|
|
|
-(z - 3) |
|
|
|
|
ds = òò |
|
3 - z |
|
|
|
|
dxdy = |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
|
|||||||||||||||||||||||||||||||||
|
|
2(x |
|
|
|
|
|
|
) |
|
|
|
|
3- z |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
2 |
+ y |
2 |
|
|
|
|
|
σ xy |
2(x2 + y2 )× |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
(x2 + y2 ) |
|
|
|||||
19
=σòòxy dxdy = 4 ×π ×9 = 4 π.
6.Соленоидальноеполе.Потенциальноеполе.Гармоническоеполе.
Векторное поле a (M ) , заданное в области Ω , называется соленоидальным, если в каждой точке M Ω справедливо:
div a (M ) = 0.
Задача1.Установить,чтоплоскоевекторноеполе
a (M ) = (-y + 2)i + (x - 3) j
соленоидально,инайтивекторныелинииэтогополя. Решение.Вычислим div a (M ) :
div a (M ) = ¶ (-y + 2) + ¶ (x - 3) = 0. ¶x ¶y
Следовательно, данное поле соленоидально. Найдем векторные линии этого поля. Составим дифференциальноеуравнениевекторныхлиний.
dx |
= |
dy |
. |
-y + 2 |
|
||
|
x - 3 |
||
Разделяяпеременныеиинтегрируя,получаем (x - 3)dx = (- y - 2)dy,
(x - 3)2 + ( y - 2)2 = C2.
Итак, семейство векторных линий представляет собой семейство концентрических окружностей с центромвточке(3.2).Векторныелиниизамкнуты.
Векторное поле a (M ) , заданное в области Ω , называется потенциальным, если оно может быть
представленоввиде
a (M ) = gradu (M ) ,
где u (M ) -скалярнаяфункция,называемаяпотенциаломвекторногополя a (M ) .
Необходимое и достаточное условие существования в области потенциального векторного поля
a (M ) :
rot a (M ) º 0.
Правило нахождения потенциала векторного поля. Для нахождения потенциала u (M ) = u (x, y, z) векторногополя
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com
a (M ) = P (M )i + Q (M ) j + R (M )k
применяетсяформула
òòP (M )dx + Q(M )dy + R (M )dz = òdu (x, y, z) =u (x, y, z)− u (x0 , y0 , z0 ).
MM0
Эта формула дает возможность найти потенциал u (x, y, z) векторного поля a (M ) с точностью до постоянного слагаемого u (x0 , y0 , z0 ). Так как линейный интеграл в потенциальном поле не зависит от
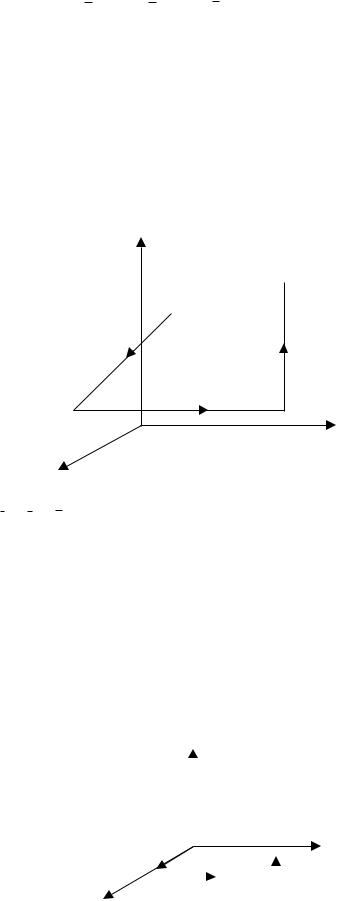
пути интегрирования, то на практике чаще всего в качестве такого пути в формуле (5.1) берут ломаную M0 ABM (рис. 6.1) , звенья которой параллельны соответствующим координатным осям. Тогда формула (6.1)пишетсятак
u (x, y, z) = òxx0 P (x, y0 , z0 )dx + òyy0 Q (x, y, z0 )dy + òzz0 R (x, y, z)dz.
z
M (x, y, z)
M0 (x0 , y0 , z0 )
Рис.6.1.
A(x, y0 , z0 ) |
B (x0 , y, z) |
0 |
y |
x
Задача2.Доказать,чтовекторноеполе a = xi + yj + zk
являетсяпотенциальныминайтиегопотенциал.
Решение.Поле будетпотенциальным,если rot a ≡ 0 .Найдемроторвекторногозаданногополя:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
j |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
rot a(M ) = |
∂ |
|
∂ |
|
∂ |
|
≡ 0. |
|
|
|
|
|
|
|
|
|
|
|||||||
∂x |
|
∂y |
|
∂z |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
|
y |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, поле является потенциальным. Для нахождения потенциала данного поля воспользуемся |
||||||||||||||||||||||||
формулой(6.2), гдевыберемточку M 0 (0,0,0),совпадающейсначаломкоординат: |
||||||||||||||||||||||||
(см.рис.6.2).Тогдаполучим |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
u(x, y, z) = ò0x xdx + ò0y ydy + ò0z zdz + C = |
x2 |
+ |
y2 |
+ |
z2 |
+ C. |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 0 (0,0,0 |
|
) 0 |
|
|
|
|
|
M (x, y, z) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
B(x, y,0) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
A(x,0,0) |
|
|
|
|
||||||||
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com

Интерес представляет изучение векторных полей, одновременно являющихся потенциальными и соленоидальными.
Пустьвекторноеполе a = a(M ) задановнекоторойпространственнойобласти D .Ононазывается
гармоническим(илилапласовым),если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
rot a(M ) = 0 и diva(M ) = 0 |
|
|
M D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Итак,гармоническоеполеобладает свойствамикакпотенциального,такисоленоидальногополя.Для |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
гармонического полясправедливо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
diva(M ) = divgradu(x, y, z) = |
|
|
u = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
¶2u |
+ |
|
¶2u |
+ |
¶2u |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.3) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
¶x2 |
|
¶y2 |
¶z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Уравнение(5.3)называетсяуравнениемЛапласа,аоператор |
-операторомЛапласаилапласианом. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Гармоническоеполеполностьюопределяетсяскалярнымпотенциалом u(x, y, z),которыйявляется |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
решениемуравнения(6.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Задача3.Показать,чтополевектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
являетсягармоническим (т.е. соленоидальным и потенциальным). Найти потенциал этого поля ( |
r |
- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
радиус-векторточки M ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Решение.Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a = |
|
|
r |
|
|
|
= |
|
|
xi |
+ yj |
|
+ zk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
r3 |
|
|
(x2 + y2 + z2 )32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (x2 |
+ y2 + z2 )−32 |
|
|
|
x(x2 + y2 |
+ z2 )−52 × 2x + (x2 + y2 + z2 )−32 |
|
|||||||||||||||||||||||||||||||||||||
div a = |
¶P |
+ |
|
¶Q |
|
+ |
|
¶R |
- |
3 |
- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
¶y |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
¶x |
|
|
|
|
|
|
|
¶z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
- |
3 |
y(x2 + y2 + z2 )−52 × 2y + (x |
2 + y2 + z2 )−32 - |
3 |
z(x2 + y2 + z2 )−52 × 2z = 0 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Значит,полевектора a(M ) -соленоидальное. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Далеевычисляем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
||||
rot a = |
|
|
|
|
|
|
|
|
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ |
|
|
= |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
¶z |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
x(x2 + y2 + z2 )−32 |
y(x2 + y2 + z2 )−32 |
|
|
z(x2 + y2 + z2 )−32 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
é |
|
|
3 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
− |
5 |
|
|
|
|
|
3 |
|
2 |
|
|
|
|
2 |
|
|
2 |
|
−5 |
|
|
ù |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
= |
ê- |
|
|
|
|
(x |
|
|
+ y |
|
+ z |
|
|
) |
|
|
2 |
|
× 2yz + |
|
|
|
(x |
|
+ y |
|
+ z |
|
|
|
) |
|
2 |
× 2zyúi |
+ |
|
|
|
|
|||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
||||||
|
é |
|
|
3 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
− |
5 |
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
−5 |
|
|
ù |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
+ |
ê- |
|
|
|
|
(x |
|
|
+ y |
|
|
+ z |
|
|
) |
|
|
2 |
|
× 2zx + |
|
|
|
(x |
|
+ y |
|
+ z |
|
|
) |
|
2 |
|
× 2xzú j |
+ |
|
|
|
|
||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|||||
|
é |
|
|
3 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
− |
5 |
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
−5 |
|
|
ù |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
+ |
ê- |
|
|
|
|
(x |
|
|
+ y |
|
|
+ z |
|
|
) |
|
|
2 |
|
× 2xy + |
|
|
|
(x |
|
+ y |
|
+ z |
|
|
|
) |
|
2 |
× 2yxúk |
= 0 |
|
|
|
|||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно,поле a(M ) -потенциальное. Находимпотенциалполя a(M )
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com

|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
z |
|
|
||||
u(x, y, z) |
= òP(x, y0 , z0 )dx + òQ(x, y, z0 )dy + òR(x, y, z)dz = |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
z0 |
|
|
||||
x |
|
|
|
xdx |
|
|
|
|
|
|
|
y |
ydy |
|
|
z |
|
|
|
zdz |
|
|
||||||||||
= ò |
|
|
|
|
|
|
|
|
|
+ ò |
|
|
+ ò |
|
|
|
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
3 |
|
|||||||||||||
x0 (x2 |
+ y2 + z2 ) 2 |
|
|
|
y0 (x2 |
+ y2 + z2 ) 2 |
|
|
z0 |
|
(x2 + y2 + z2 ) |
2 |
|
|||||||||||||||||||
= - |
|
|
|
|
|
|
1 |
|
|
|
|
+ |
|
|
|
|
|
|
1 |
|
= - |
1 |
+ |
|
1 |
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x2 + y2 + z2 |
|
|
|
|
|
|
|
x02 + y02 + z02 |
r |
r0 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
ОператорГамильтона. |
|
|
||||||||
Оператор |
Гамильтона или |
так |
называемый |
|
набла-вектор Ñ |
|
- это символический вектор, |
|||||||||||||||||||||||||
определяемыйвдекартовойсистемекоординатвыражением |
|
|
||||||||||||||||||||||||||||||
Ñ = |
¶ |
|
|
¶ |
|
|
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
i |
+ |
|
|
j + |
|
|
k. |
|
(7.1) |
|
|
|
|
|
|
|||||||||||||||||
¶x |
|
¶z |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
При помощи Ñ -вектора основные операции векторного анализа (нахождение скалярного поля, дивергенцииироторавекторногополя)записываютсяследующимобразом:
gradu = Ñu |
(7.2) |
div a = (Ñ × a ) |
(7.3) |
rot a = Ñ ´ a |
(7.4) |
Нижеприведенрядформул,полученныхприпомощиоператора Ñ . grad{u1 ×u2 }= Ñu1u2 = u1Ñu2 + u2Ñu1 = u1 gradu2 + u2 grad u1 , divua = Ñ × ua = uÑa + aÑu = u div a + a grad u,
rot ua = Ñ ´ ua = (Ñu)´ a + u(Ñ ´ a ) = (grad u)´ a + u rot a = u rot a - a ´ gradu.
Задача1.ЗаписатьприпомощиоператораГамильтона
divgradu = u(x, y, z). |
|
|
|
|
|
|
|
|
|
||||||
Решение.Имеем |
|
|
|
|
|
|
|
|
|
|
|||||
divgradu = Ñ × grad u = Ñ × (Ñu) = Ñ2u = Du, |
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
æ |
¶2 |
|
¶2 |
|
¶2 |
ö |
|||
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
2 + |
|
2 |
+ |
|
2 |
|||
где Ñ = D -операторЛапласа çD = |
¶x |
¶y |
¶z |
÷ |
|||||||||||
|
|
|
|
|
|
è |
|
|
|
|
|
ø |
|||
|
|
dx |
|
= |
dy |
= dz |
|
|
|
|
|
|
|
|
|
- |
Jy |
|
Jx |
0 |
|
|
|
|
|
|
|
|
|
||
2πρ 2 |
|
2πρ 2 |
|
|
|
|
|
|
|
|
|
|
|||
или
ì dx = dy
ïí- y x ïîdz = 0
Послеинтегрированияполучим
x2 + y2 = C12 ,
z = C2
Векторными линиями рассматриваемого поля будут концентрические окружности радиуса C1 с центромнаоси OZ ,расположенные вплоскости Z = C2 .
Задача2.Имеетсяплазменныйшнуркруговогосечениярадиуса a ,покоторомутечетэлектрический
токплотности
æ x2 |
+ y2 ö32 |
|||
ç |
|
|
|
÷ |
|
|
2 |
||
J = J0 ç |
a |
÷ |
||
è |
|
|
ø |
|
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com
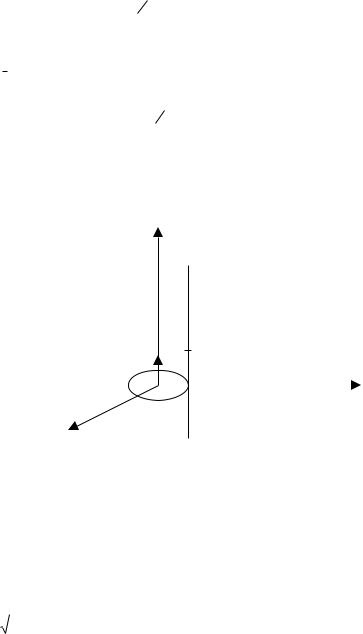
Определитьполныйток,проходящийчерезсечениеплазменногошнура.
Решение. Вдоль оси плазменного шнура направим осьOZ (рис. 8.1). Вектор плотности тока имеет
вид
|
|
|
|
|
|
|
|
|
|
|
æ x2 |
|
+ y2 ö32 |
|
|
|
|
||||||||||
J = 0 × i + |
0 × j + J |
ç |
|
|
|
|
|
|
|
|
÷ |
|
|
k , |
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||
0 ç |
|
|
a |
|
÷ |
|
|
|
|||||||||||||||||||
нормаль |
|
|
|
|
|
|
è |
|
|
|
|
|
ø |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n 0 = 0 × i |
+ 0 × |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
j |
+1× k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Полныйток |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
2 |
|
|
|
2 |
|
ö32 |
|
|||||
I = òò(J , n |
0 |
|
|
|
|
|
|
|
|
ç |
x |
|
+ y |
|
|
÷ |
|
ds, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
|
)ds = J0 òòç |
|
|
|
|
a |
|
|
|
÷ |
|
||||||||||||||||
Σ |
|
|
|
|
|
|
|
Σ è |
|
|
|
|
|
|
|
|
ø |
|
|
||||||||
где круградиуса a .Переходякполярнымкоординатам,получаем
|
3 |
2π |
a |
4 |
|
ρ 4 |
|
a |
|
2πa5 |
|
|
|
|
|
|
|||||||
I = J0 òòρ |
|
× dρdϕ = J0 òdϕò ρ |
|
dρ = 2π |
|
|
0 |
= |
|
J0 . |
|
|
|
5 |
5 |
||||||||
Σ |
|
0 |
0 |
|
|
|
|
|
|
||
z
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
= k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
(M ) напряженности магнитного поля, |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Задача 3. Определить ротор вектора |
|
|
|
|
образованного |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
H |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
электрическим током силой I , |
|
текущим по бесконечно длинному проводу, |
в точке M , |
лежащей |
вне |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
провода(рис.8.2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(M ) |
|
|||||||||
Решение. Выберемсистемукоординаттак,чтобыось OZ совпадаласпроводником.Тогда |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
H |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
определяетсяформулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
(M ) = |
|
− I |
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
H |
|
|
|
|
yi |
+ |
|
|
|
|
xj |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2πρ |
2 |
|
2πρ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где ρ = |
|
|
|
|
|
|
–расстояниеотточки M (x, y, z) дооси OZ .Поформуленайдем rot |
|
(M ): |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x2 + y2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
H |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é I |
|
|
æ |
|
|
x |
ö |
|
I |
|
|
|
æ |
|
|
|
y |
öù |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
¶ |
|
|
|
|
|
|
|
|
|
¶ |
|
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ |
|
|
|
|
¶ |
|
|
|
|
||||||||||||||||||||||||||
rot H (M ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
÷ |
|
|
|
|
|
ç |
|
|
|
|
|
|
|
÷ |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= i × 0 + |
j × 0 + k ê |
× |
|
|
2 |
|
|
- |
|
× |
|
|
|
2 |
|
|
|
|
|
= |
||||||||||||||||||||||||||||||
|
|
¶x |
|
|
|
¶y |
|
|
|
|
|
|
¶z |
|
ç |
|
+ y |
2 ÷ |
2π |
|
|
ç- |
x |
+ y |
2 ÷ú |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë2π |
|
¶x è x |
|
ø |
|
|
|
¶y è |
|
øû |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
- Iy |
|
|
|
|
Ix |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2πρ 2 |
|
|
2πρ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
I |
é x2 |
+ y2 - 2x2 |
|
|
x2 |
|
+ y2 - 2y2 ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
úk |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 + y2 )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
2π ê (x2 + y2 )2 |
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com
|
|
|
|
|
|
z |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M (x, y, z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.8.2. |
|
|
|
|
|
|
L2 |
|
|
|
L1 |
||
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
y |
||||||
|
|
|
||||||||||
|
|
|
|
x |
|
|
|
|
||||
|
|
Итак, в любой точке поля кроме точек, лежащих на оси OZ , по которой протекает ток, |
||||||||||
rot |
|
(M ) = 0 . |
|
|
|
|
||||||
H |
|
|
|
|
||||||||
|
|
Наоси OZ вектор |
|
(M ),а,следовательно,и rot |
|
(M ),теряютсмысл. |
||||||
|
|
H |
H |
|||||||||
|
|
Задача 4. Найти циркуляцию вектора |
|
(M ) |
напряженности магнитного поля в условиях |
|||||||
|
|
H |
||||||||||
предыдущей задачи: 1) по кривой L1 , не окружающей проводник; 2) по окружности L2 , окружающей
проводник,находящийсявплоскости,перпендикулярнойоси OZ ,сцентромнаэтойосиирадиусомравным
R .(рис.8.2)
Решение. 1) Пусть L1 – произвольный замкнутыйконтур, ограничивающийобласть, через которую непроходитось OZ .Таккаквовсехточкахэтойчастиполя rot H (M ) = 0 ,тополучим
òH × dr =òòrot H × n 0 ds = 0,dr = τ 0 × dl
L1 |
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
Пусть L2 – окружность радиуса R , лежащая в плоскости, перпендикулярной оси OZ с |
|||||||||||||||
центромнаэтойоси.Тогдаполучим |
|
|
|
|
|
|
|
|
|
|
|
||||||
ò |
|
× dr |
= ò- |
Iy |
dx + |
Ix |
|
dy = |
I |
|
ò xdy - ydx = |
I |
|
× 2S = |
I |
|
× 2πR2 = I. |
H |
|
||||||||||||||||
2 |
2πR |
2 |
2πR |
2 |
2πR |
2 |
2πR |
2 |
|||||||||
L2 |
|
|
L2 |
2πR |
|
|
|
L2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Итак, òH × dr =I.
L2
Отличие от нуля циркуляции во втором случае можно объяснить тем, что не во всех точках области поля,ограниченнойконтуром L2 ,роторвектора H равеннулю.
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com
ЛИТЕРАТУРА
1.Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функциикомплексногопеременного.–М.:Наука,1981–448с.
2.Специальные разделы математическогоанализа: Сборникзадач поматематике длявтузов. Ч. П. Подред.А.В.ЕфимоваиБ.П.Демидовича.–М.Наука,1986–366с.
3.КрасновМ.Л.,КиселевА.И.,МакаренкоГ.И.Векторныйанализ.–М.:Наука,1978.–159с.
4.Глатенок И. В., Заварзина И.Ф. Методические указания к практическим занятиям по курсу «Высшаяматематика»,«Теорияполя».М.–1989г.–39с.
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com
