Вставка і видалення
1. Для того, щоб вставити новий елемент в дерево, необхідно знайти для нього місце. Для цього, починаючи з кореня, порівнюємо значення вузлів (Y) із значенням нового елементу (New). Якщо New<Y, то йдемо по лівій гілці, інакше - по правій гілці. Коли дійдемо до вузла, з якого не виходить потрібна гілка для подальшого пошуку, це означає, що місце під новий елемент знайдене.
Дуже часто операція додавання приводить до незбалансованого дерева.
Наприклад. Щоб вставити 18 в дерево на малюнку ми спочатку повинні знайти це число. Пошук приводить нас у вузол 16, де благополучно завершується. Оскільки 18 > 16, ми просто додає вузол 18 як правий нащадок вузла 16 (мал. 20).
На цьому прикладі добре видно, як виникає незбалансованість дерева. Якщо дані поступають в зростаючому порядку, кожен новий вузол додається праворуч від останнього вставленого. Це приводить до одного довгого списку. Звернете увагу: чим більш "випадкові" дані, що поступають, тим більше збалансованим виходить дерево.
Мал. 20. Бінарне дерево після додавання вузла 18
2. При видаленні вузла з дерева можливі три ситуації:
1. Вузол, що видаляється, є листом - просто видаляємо посилання на нього;
Видалення листа з ключем key:
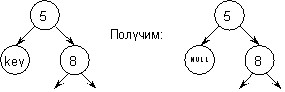Мал.
20
2. З вузла, що видаляється, виходить тільки одна гілка;
Видалення вузла того, що має одного нащадка:
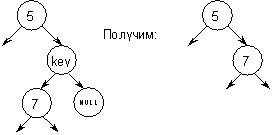Мал.
21
3. Видалення вузла, що має двох нащадків, значно складніше. Якщо key – вузол, що виключається, то його слід замінити вузлом w, який містить або найбільший ключ в лівому поддереве, або найменший ключ в правому поддереве. Такий вузол w є або листом, або найправішим вузлом поддерева key, у якого є тільки лівий нащадок:
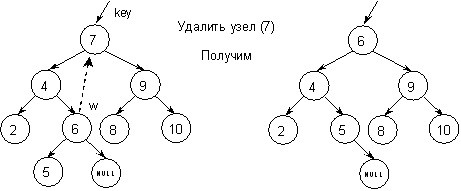
Мал. 22
Таким чином, якщо з вузла, що видаляється, виходить дві гілки (в даному випадку на місце вузла, що видаляється, треба поставити або найправіший вузол лівої гілки, або найлівіший вузол правої гілки для збереження впорядкованості дерева).
Наприклад, якщо з дерева на мал. віддаляється вузол 20, його спочатку потрібно замінити на вузол 37. Це дасть дерево, зображене на мал. 3.5. Міркування тут приблизно наступні. Нам потрібно знайти нащадка вузла 20, праворуч від якого розташовані вузли з великими значеннями. Таким чином, нам потрібно вибрати вузол з найменшим значенням, розташований праворуч від вузла 20. Щоб знайти його, нам і потрібно спочатку спуститися на крок управо (потрапляємо у вузол 38), а потім на крок вліво (вузол 37); ці двокрокові спуски продовжуються, поки ми не прийдемо в кінцевий вузол, лист дерева.
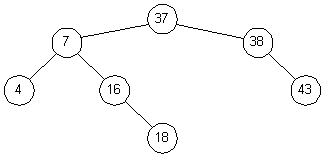
Мал. 23. Бінарне дерево після видалення вузла 20 Контрольні запитання:
Як сформувати дерево з цілих чисел
Як здійснити додавання
Як здійснити видалення по ключу
Як здійснювати обходи Left-root-right; Root-left-right; Left-right-root.
Література:
Иванова Г.С., Ничушкина Т.Н., Пугачев Е.К. И21 Объектно-ориентированное программирование: Учеб. для вузов/ Под ред. Г.С. Ивановой. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. - 320 с, ил.
Архангельский А.Я. , Программирование в Delphi 7. М.: ООО «Бином-Пресс», 2003 г. 1152 с.: ил.
Колосов С.В.,Программирование в среде Delphi. Учеб. пособие для студентов специальностей «Автоматизированные системы обработки информации» и «Автоматическое управление в технических системах» БГУИР., - Мн.:БГУИР, 2005,-164 с: ил. 34.
Пестриков В. М., Маслобоев Л. Н, П28 Delphi на примерах, — СПб.: БХВ-Петербург, 2005. — 496 с: ил. ISBN 5-94157-713-3
Дарахвелидзе П. Г., Марков Е. П.Программирование в Delphi 7. — СПб.: БХВ-Петербург, 2003. — 784 с: ил.
Алексеев В.Е., Таланов В.А. Графы и алгоритмы. Структуры данных. Модели вычислений БИНОМ. Лаборатория знаний, Интернет-университет информационных технологий - ИНТУИТ.ру, 2006