Размер атома водорода

Рассмотрим частицу, «запертую» в одномерной области размером l. Согласно принципу неопределенности её . Если энергия Eчастицы превышает минимально возможную , то её импульс можно записать как p=<p>+ . Уменьшаем при этом <p> и p Точное положение электрона в атоме невоз-можно, т.к. тогда . Для оценки наименьшей возможной энергии электрона полагаем и . Тогда и Отсюда видно почему электрон не падает на ядро. Энергию E составляют два слагаемых: при уменьшении r возрастает значение отрицательного слагаемого (т.е. сила притяжения), но вместе с ним возрастает (в большей степени) значение кинетической энергии, что не дает электрону упасть на ядро и играет роль силы отталкивания. Таким образом, размер атома водорода - компромисс кулоновских сил притяжения и сил отталкивания.

Состояние частицы

Пусть нерелятивистская частица движется в стационарном силовом поле. Для теоретического описания движения должны быть определены:

1. величины, задающие состояние частицы;

2. уравнения изменения состояния частицы во времени;

3. величины, доступные измерению и способы измерений (для сравнения выводов теории и опытных фактов).

В классической теории:

1. состояние частицы задают: скорость, импульс, ускорение, сила и пр.;

2. изменения величин во времени задаются динамическими уравнениями, результатом расчетов является точное описание состояния частицы в некоторый момент времени.

3. величины доступны измерению.

В квантовой теории:

1. в силу соотношения неопределенностей определение состояния частицы через координату и импульс теряет смысл (эти величины не имеют точного значения);

2. «объяснение» явлений происходит на основе создания математического формализма, следствия которого совпадают с результатами опытов;

3. тот факт, что отдельная микрочастица обладает волновыми свойствами, был истолкован так: движение микрочастицы подчиняется вероятностным законам. Распределение вероятности, характеризующей это движение, проявляется в результате регистрации достаточно большого числа частиц, и оно оказывается таким же как распределение интенсивности волны (больше интенсивность волны – больше регистрируемое число частиц);

4. целью является не точное предсказание событий, а определение вероятности этих событий. По значениям вероятностей можно найти средние значения величин, доступных эксперименту.

5. в соответствии с корпускулярно-волновым дуализмом состояние частицы задают пси-функцией ψ(r;t), которая является комплексной величиной, формально обладает волновыми свойствами и позволяет находить все вероятности.

Например, в заданном объеме dV в момент времени t вероятность нахождения частицы , где 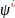- комплексно сопряженная функция. Отсюда плотность вероятности(т.е. вероятность нахождения частицы в единице объема) экспериментально наблюдаемая, тогда как ψ-функция величина комплексная и ненаблюдаемая. функция должна соответствовать условию нормировки:

, где интеграл берется по всему пространству или по той области, где 0 (частица в области находится обязательно).

• Физический смысл имеет не сама ψ-функция, а квадрат её модуля , наблюдаемый экспериментально. Однако, т.к. волновая теория объясняет волновые явления интерференцией волн, а не их интенсивностей, квантовая теория связывает волновые свойства с ψ,а не с .