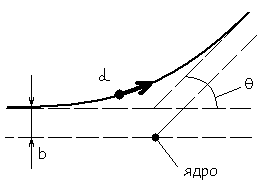
Атом Резерфорда-Бора. Формула Резерфорда

В 1911 г. Резерфорд по результатам опытов прохождения -частиц сквозь тонкую фольгу обнаружил, что:

1

α

) основная часть -частиц испытывает незначительное отклонение ≤3°;

2) крайне малое число -частиц испытывает неожиданно большое отклонение > 90°, откуда следует, что атом должен содержать ядро, размеры которого ~ в 10⁵ раз меньше размеров атома и составляют порядка 10^-12 см;

3) траектория полета -частицы имеет вид:

b – прицельный параметр, - угол отклонения;

4) формула распределения рассеянных -частиц: , где q и q₀ – заряды налетающей частицы и ядра; К – кинетическая энергия частицы вдали от ядра.

5) прицельный параметр b измерению не доступен и Резерфорд связал его изменение в интервале (b, b+db) с изменением угла рассеивания в интервале ( , +d ), а затем и с телесным углом dΩ, в пределах которого заключены все углы рассеивания ( , +d ).

Тогда формула Резерфорда: , где - относительное число частиц, имеющих прицельный параметр b в интервале (b, b + db), рассеянных в телесном угле dΩ под углом к первоначальному направлению их движения, n – число ядер металла фольги на единицу её поверхности.

• Для определения относительного числа частиц, рассеянных в интервале ( ₁, ₂) формулу Резерфорда интегрируют с учетом .

• Формула Резерфорда неприменима к малым (<3°) углам.

Дифференциальное сечение

Если b изменяется в интервале (b, b + db), то изменяется в( , + d ). Рассмотрим кольцо радиуса b и ширины db. Его площадь .С учетом формула Резерфорда:

или , где – дифференциальное сечение.

• Введение упрощает расчеты.

Итак: относительное число частиц, рассеянных в интервале углов ( , +d ), равно произведению количества ядер на единице площади поверхности фольги (n) на соответствующее дифференциальное сечение.

Спектральные закономерности

Изучение спектров излучения невзаимодействующих друг с другом атомов показало, что:

1) эти спектры линейчатые(состоят из отдельных узких спектральных линий);

2) большое число спектральных линий указывает на сложную структуру атома;

3) линии расположены упорядоченно и образуют серии;

4) в 1885 г. Бальмер установил закономерность видимой серии спектра атома водорода:

, где n = 3, 4, 5, …; – циклическая частота определенной

(для каждого значения n) линии серии, R = 2,07· 10¹⁶с^-1 – постоянная Ридберга;

5) исследования привели к обнаружению других серий и к обобщению формулы Бальмера: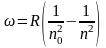 , при этом:

n₀ = 1 – серияЛаймана (ультрафиолетовая область)

n₀ = 2 – серия Бальмера (видимая область)

n₀ = 3 – серия Пашена (инфракрасная область)

n₀ = 4 – серия Бреккета ( )

n₀ = 5 – серия Пфунда( )

• При заданном значении n₀ n принимает все целочисленные значения, начиная с n₀+1.

• При , называемое границей серии.

• При n₀ = 1 и n = 2 для этой серии и . Эту спектральную линию называют резонансной линией водорода.