Примесная проводимость полупроводников
В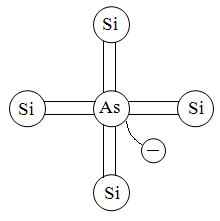
ведем
в кристалл четырехвалентногоSi
примесь пятивалентногоAs.
Один электрон атома As
останется без ковалентной связи, он
легко может стать свободным. Дырка при
этом не образуется.
Донорная примесь– примесь, создающая в полупроводнике
свободные электроны.
Электронная проводимость– проводимость полупроводника,
содержащего донорные примеси.
Такие п/п называют п/п n-типа (negative-отрицательный). Они имеют свободные
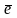и положительные ионы примеси.
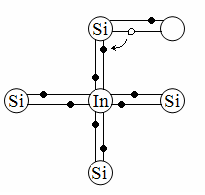При введении в
четырехвалентный Si
трехвалентного
In
образуются только три ковалентные
связи: Недостающий четвертый
атом In
захватывает у соседнего атома Si,
где образуется дырка, способная
передвигаться и участвовать в электрическом
токе.
Акцепторная примесь–примесь, создающая в п/п дырки.
Дырочная проводимость– проводимость п/п, содержащего акцепторные примеси.
Такие п/п называют п/п p-типа (positive-положительный). Они содержат дырки и отрицательные ионы примеси.
Примеси искажают поле кристаллической решетки, что приводит к возникновению примесных энергетических уровней, расположенных в запрещенной зоне.
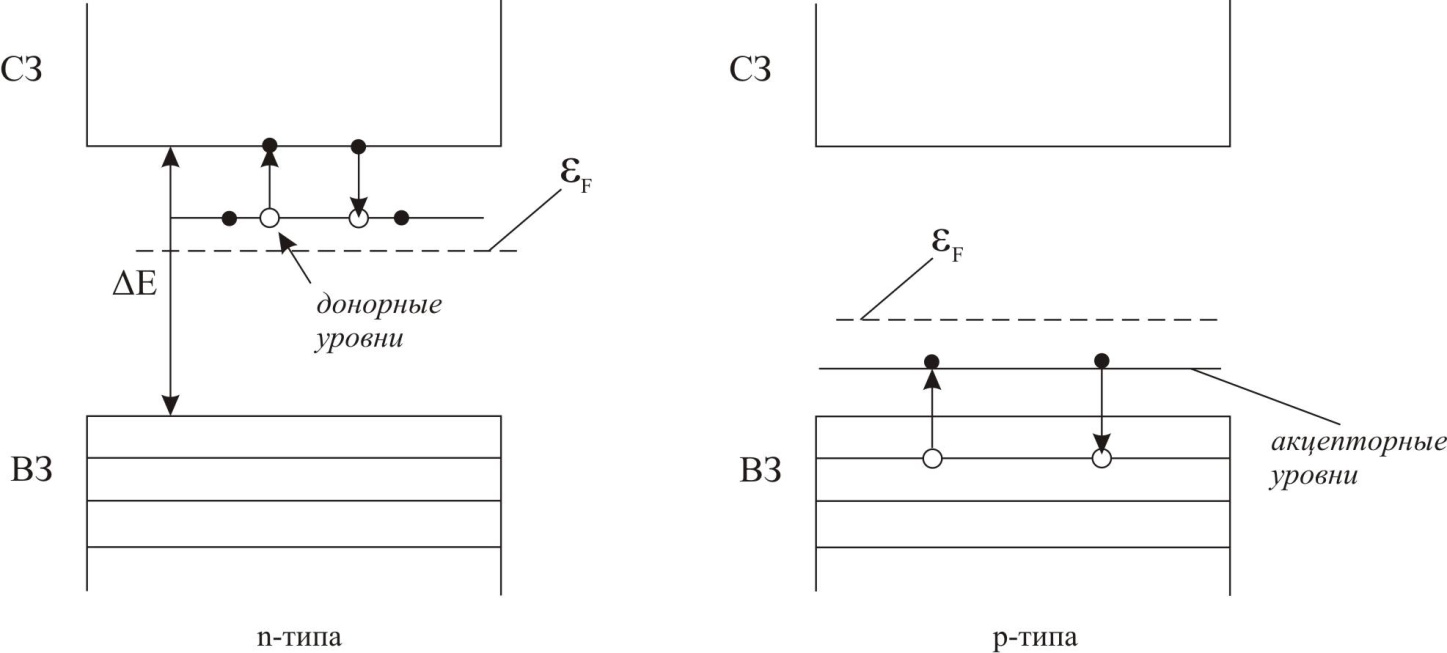
Уровень Ферми в п/п n-типа расположен в верхней половине запрещенной зоны,
р-типа – в нижней. При повышении температуры:1) уровень Ферми п/п (n и р) смещается к середине запрещенной зоны;
2) концентрация примесных носителей быстро достигает насыщения и далее все больший вклад вносит собственная проводимость, обусловленная переходом из валентной зоны в зону проводимости, т.е. при низких Т преобладает примесная проводимость, при высоких – собственная.
Электропроводность металлов
Из опытов известно,
что сопротивление проводника
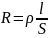, где удельное сопротивление зависит
от температуры:
и
удельное
сопротивление при
.
Согласно квантовой
теории, электрон, обладая волновыми
свойствами рассеивается на неоднородностях
кристаллической решетки и
,
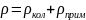где
–удельное
сопротивление, обусловленное тепловыми
колебаниями решетки,
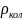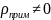– удельное сопротивление, обусловленное
примесной деформацией решетки.
Если
бы кристаллическая решетка была
идеальной, то при
Т=0
было бы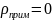
.
Согласно
классической теории металлов
,
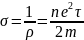где
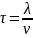- время свободного пробега электрона
в металле.
Чем больше Т, тем сильней колебания, меньше τ и
меньше
σ,
т.е. тем больше
.
Квантовая теория приводит к аналогичным выводам.
Энергия молекулы
Из опытов известно, что рентгеновские спектры тяжелых элементов не зависят от того, в состав каких химических соединений они входят. Значит, взаимодействие атомов обусловлено внешними электронами и не влияет на рентгеновский спектр атома.
В
качестве простейшего примера рассмотрим
молекулу, состоящую из двух одинаковых
атомов (например Н2).
Потенциальная энергия такой системы
-
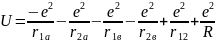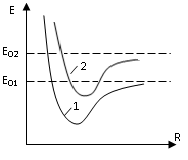
Из
уравнения Шредингера получается, что
собственные значения энергии молекулы
зависят от R,
т.е. Е=Е(R)
и
график Е(R)
имеет вид:
При этом получается семейство кривых, каждая из которых соответствует определенному квантовому состоянию электрона. Энергию, обусловленную электронной конфигурацией будем называть электронной (она вносит наибольший вклад в изменение энергии молекулы).
3)При
заданной электронной конфигурации ядра
молекулы могут различным образом
колебаться и вращаться относительно
общего центра масс. Приближенно можно
полагать, что энергия молекулы
,
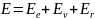где
-
электронная энергия,
-
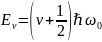колебательная энергия
(см. квантовый гермонический осциллятор).
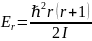– вращательная
энергия (см. ротатор). Таким образом,
полная энергия молекулы
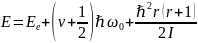
4)
Доказано, что интервал
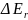между
вращатель-
ными уровнями значительно меньше интер-
вала между колебательными уровнями, и
они оба значительно
меньше интервала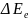
между электронными уровнями. Схема энер-гетических уровней двухатомной молекулы: