Тормозное рентгеновское излучение

При уравнение Эйнштейна: , что хорошо согласуется и с обратным фотоэффекту процессом: преобразованием кинетической энергии электрона в квант излучения при резком торможении электронов в металле. В рентгеновской трубке электроны излучаются катодом, ускоряются напряжением Uанод – катод , попадают на анод, резко тормозятся и вызывают рентгеновское излучение. Его спектр сплошной, семейство интенсивностей для различных Uимеет вид:

Н аличие коротковолновой границы спектра обусловлено тем, что энергия кванта конечна и или U

Связь U, и ħ позволяет определять с высокой точностью.

Опыт Боте. Фотоны

Опыт Боте – непосредственное подтверждение существования фотонов – квантов ЭМИ. В установке Боте: Х – слабый пучок рентгеновского излучения, F – тонкая

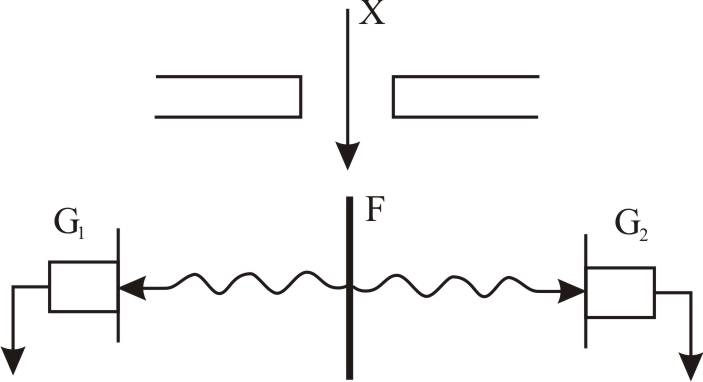металлическая фольга, и - быстродействующие счётчики. Под действием излучения X фольга Fсама становится источником излучения. Если бы энергия фольги распространялась в виде волны, то счётчики работали бы синхронно. Опыт показал, что счётчики регистрируют приход излучения в разные моменты времени(не синхронно), т.е. излучение носит квантовый характер.

По Эйнштейну фотоны:

1. обладают энергией ;

2. образуют поток излучения – свет, т.е. каждый фотон движется со скоростью c, одинаковой во всех системах отсчёта ( не существует такой системы отсчёта, в которой фотон покоился бы);

3. для релятивистской частицы . Для фотона т.е. фотон- частица без массы покоя, его естественное состояние – движение с =c

4. доказано, что фотон обладает импульсом ;

5. - волновое число. Тогда или , где - волновой вектор.

Корпускулярно-волновой дуализм

Опыты обнаруживают корпускулярные свойства света, что противоречит электромагнитной теории Максвелла.

В соотношениях и величины и характеризуют фотон как частицу, и - как волну, причём в области длинных волн фотон главным образом проявляет волновые свойства, в области коротких –корпускулярные.

С точки зрения классической физики здесь явное противоречие: невозможно представить себе частицу – волну. Приходится анализировать опытные данные, выходящие за рамки классического воображения.

Эффект Комптона

В 1923 г Комптон открыл явление, подтверждающее, что фотон обладает энергией и импульсом. Он облучал узким пучком рентгеновского излучения λ образцы, состоящие из лёгких атомов(графит, парафин, и т.д.) и обнаружил, что после рассеяния в спектре помимо излучения λ появляется излучение .Это явление получило название эффект Комптона.

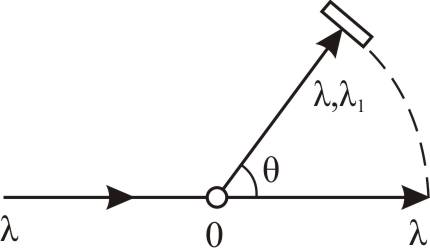
Опыт показал, что смещение зависит только от угла между исход-ным лучом и направлением на спектрограф (не зависит от λ и материала образца 0), причём с увеличением амплитуда компоненты λ уменьшается, а растёт.

Комптон предположил, что рассеивание рентге-новского кванта с изменением длины волны надо рассматривать как результат столкновения его с электроном. Смещение не зависит от материала рассеивающего образца потому, что в образцах с легкими атомами энергия связи электрона с ядром пренебрежимо мала по сравнению с энергией фотона, т.е. фотон взаимодействует с практически свободным электроном.

1. Пусть свободный покоящийся электрон взаимодействует с фотоном, поглощая всю

его энергию. Тогда по законам сохранения энергии и импульса и ,

где m–масса электрона, υ-его скорость после взаимодействия. Тогда или

υ=2с , что невозможно. Значит, всю энергию фотона свободный электрон получить

не может и в результате взаимодействия появляется новый фотон и электрон

“отдачи”.

2. Пусть фотон с и взаимодействует с покоящимся свободным

электроном с энергией покоя и импульсом . В результате взаимодействия получается новый фотон с , и и

электрон с E=γ· и , где –скорость электрона,

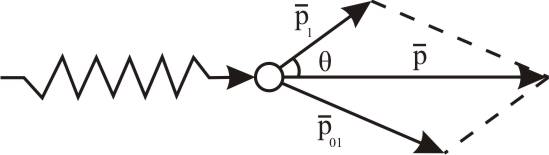
3. По закону сохранения энергии: или = .

Возведём в квадрат : (1)

По закону сохранения импульса и теореме косинусов: или, с учётом и , или (2).

Вычтем (1) из (2): . Поделим на и с учётом

получим или Откуда или и с учётом или, с учётом , . или или , где -комптоновская длина волны для частицы массы

• Для электрона см.