
- •Квантовая физика
- •Квантовые свойства электромагнитного излучения (эми) Тепловое излучение (ти)
- •Фотоэффект
- •Тормозное рентгеновское излучение
- •Корпускулярно-волновой дуализм
- •Эффект Комптона
- •Атом Резерфорда-Бора. Формула Резерфорда
- •Дифференциальное сечение
- •Спектральные закономерности
- •Постулаты Бора
- •Опыт Франка и Герца (1913)
- •Модель атома Бора
- •Спектральные серии водородоподобных систем
- •Магнитный момент атома водорода
- •О теории Бора
- •Волновые свойства частиц
- •Опыты Дэвисона и Джермера (1927)
- •Опыты Томсона и Тартаковского
- •Другие опыты
- •Парадоксальное поведение микрочастиц
- •Критерий классического описания
- •Принцип неопределенности
- •Опыт со щелью
- •Размер атома водорода
- •Состояние частицы
- •Принцип суперпозиции
- •Уравнение Шредингера
- •Стационарные состояния
- •Квантование
- •Частица в прямоугольной яме
- •Квантовый гармонический осциллятор
- •Колебания в молекуле
- •П отенциальные барьеры
- •Туннельный эффект
- •Средние значения физических величин
- •Операторы
- •Основные постулаты квантовой теории
- •Квантование момента импульса
- •П роекция момента импульса
- •Ротатор
- •Квантование атомов
- •Плотности распределения вероятности
- •Правило отбора
- •Тонкая структура спектральных линий
- •Спин электрона
- •Полный момент импульса электрона
- •Механический момент многоэлектронного атома
- •Правила отбора
- •Принцип Паули
- •О периодической системе Менделеева
- •Характеристические рентгеновские спектры
- •Магнитные свойства атома
- •Опыт Штерна и Герлаха
- •Спиновой магнитный момент
- •Полный магнитный момент атома
- •Эффект Зеемана(1896)
- •П ростой эффект Зеемана
- •Сложный эффект Зеемана
- •Эффект Пашена-Бака
- •Электронный парамагнитный резонанс
- •Атомное ядро Некоторые сведения о ядре
- •Размеры ядра
- •Спин ядра(I)
- •Масса и энергия связи ядра
- •Удельная энергия связи
- •Механизм взаимодействия нуклонов
- •Модели ядра
- •Радиоактивность
- •Закон радиоактивного распада
- •Типы радиоактивности
- •Ядерные реакции
- •Выход ядерной реакции
- •Энергия реакции
- •Квантовые статистики (кс)
- •Фазовые ячейки
- •Квантовые распределения
- •Число фазовых ячеек
- •Распределение частиц
- •Свободные электроны в металле
- •Энергия Ферми
- •Зонная теория твердого тела Предпосылки возникновения зонной теории
- •Образование электронных зон
- •Характеристика энергетических зон
- •Металлы, диэлектрики и полупроводники
- •Собственная проводимость полупроводников (п/п)
- •Примесная проводимость полупроводников
- •Электропроводность металлов
- •Энергия молекулы
- •Элементарные частицы
- •Фундаментальные взаимодействия
- •Хронология
- •Систематика
- •Античастицы
- •Законы сохранения
- •Заряды элементарных частиц
- •Странность
- •Шарм (очарование) и красота (прелесть)
- •Четность
- •Изотопический спин
- •Кварковая модель адронов
- •Современная картина мира
Квантование момента импульса
Момент импульса в квантовой теории:
 одна
из важнейших характеристик движения;
одна
из важнейших характеристик движения;сохраняется, если система изолирована или движется в центральном силовом поле;
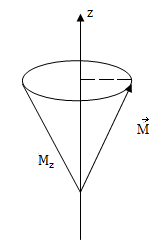
точно может быть задано значение только одной из проекций, остальные – не определены и направление неопределено.
Если определена,
например,
 ,
то
,
то
 как-то размазан по образующим конуса,
как-то размазан по образующим конуса,
Mx и My не определены.
M2 можно определить из уравнения
 ψ
= M2ψ;
ψ
= M2ψ;доказано, что M2 = 𝑙(𝑙+1)ħ2, где 𝑙 = 0, 1, 2,… - орбитальное квантовое число.
Тогда
 – дискретная (квантованная) величина;
– дискретная (квантованная) величина;
 ,
,
,
,
 не зависят от выбора точки отсчета 0,
тогда как классический
не зависят от выбора точки отсчета 0,
тогда как классический
= зависит;
зависит только от направления координатных осей.
П роекция момента импульса
Из
=
 и
ψ
=
ψ
⇒
ψ =
ψ.
Из этого уравне-
и
ψ
=
ψ
⇒
ψ =
ψ.
Из этого уравне-
ния
 ,
где m
= 0,
,
где m
= 0,
 1,
1,
 …
- магнитное
квантовое число. Направление
оси Z
выбрано произвольно, значит
квантуется
на
…
- магнитное
квантовое число. Направление
оси Z
выбрано произвольно, значит
квантуется
на
любое направление.
Из
 и
и
 видно, что М и Мzквантованы
(на рис. l=2).
видно, что М и Мzквантованы
(на рис. l=2).
Схематически
 ,
соответствующую квантовому числу l
можно рассматривать как суперпозицию
,
соответствующую квантовому числу l
можно рассматривать как суперпозицию
 ,
отличающихся числом m,
т.е. состояние
с заданным l
является вырожденным по m.
,
отличающихся числом m,
т.е. состояние
с заданным l
является вырожденным по m. и (при заданном l)
m
принимает 2l+1
значений:
и (при заданном l)
m
принимает 2l+1
значений:
-l,… , -1,0,1,…, l и образует спектр значений Мz.
l задает как модуль М момента импульса, так и все возможные значения его
проекций
Мz.
Пример:
l=2:
 ;
Мz
= 0,±1
,
±2
;
Мz
= 0,±1
,
±2
Итак:
 -
пространственное
квантование.
-
пространственное
квантование.
Ротатор
Ротатор- неизменяемая вращательная система.
В классической
физике энергия вращения твердого тела
 ,
где М- момент импульса тела, I-
момент инерции тела относительно оси
вращения.
,
где М- момент импульса тела, I-
момент инерции тела относительно оси
вращения.
В
квантовой физике :
 .
Собственные значения
.
Собственные значения
 квантованы :
квантованы :
 .
Значит, собственные значения
.
Значит, собственные значения также квантованы и
также квантованы и
 ,
где r=0,1,2,3,…-вращательное
квантовое число.
,
где r=0,1,2,3,…-вращательное
квантовое число.
r вместо l подчеркивает, что это выражение характеризует вращение молекул.
Интервал между вращательными уровнями энергии ротатора (молекулы) растет с увеличением r:
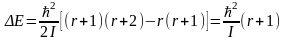 .
.
При
этом действует правило
отбора:
 .
.
Ч астоты
линий спектра при переходах :
астоты
линий спектра при переходах : ,
где r-
квантовое число уровня на
который
происходит переход.
,
где r-
квантовое число уровня на
который
происходит переход.
Для двухатомной молекулы I берется относительно оси ОО´, проходящей через центр масс С нормально к линии, соединяющей ядра атомов. При этом
 ,
где
,
где
 -
приведенная масса, m1
и m2-
массы атомов молекулы, d
– расстояние между ядрами атомов
молекулы. Уровни энергии и линии
спектров вращения молекул:
-
приведенная масса, m1
и m2-
массы атомов молекулы, d
– расстояние между ядрами атомов
молекулы. Уровни энергии и линии
спектров вращения молекул:
Зная
 ,
можно определить I
молекулы и при известных m1
и m2
вычислить d.
В общем случае молекула одновременно
вращается и колеблется, что приводит к
появлению колебательно-вращательных
спектров.
Линии спектра отстоят друг от друга
на
.
При переходе с излучением энергия
,
можно определить I
молекулы и при известных m1
и m2
вычислить d.
В общем случае молекула одновременно
вращается и колеблется, что приводит к
появлению колебательно-вращательных
спектров.
Линии спектра отстоят друг от друга
на
.
При переходе с излучением энергия
 ,
где
,
где
 и
и
 -
соответственно энергии колебаний и
вращения молекулы.
-
соответственно энергии колебаний и
вращения молекулы.
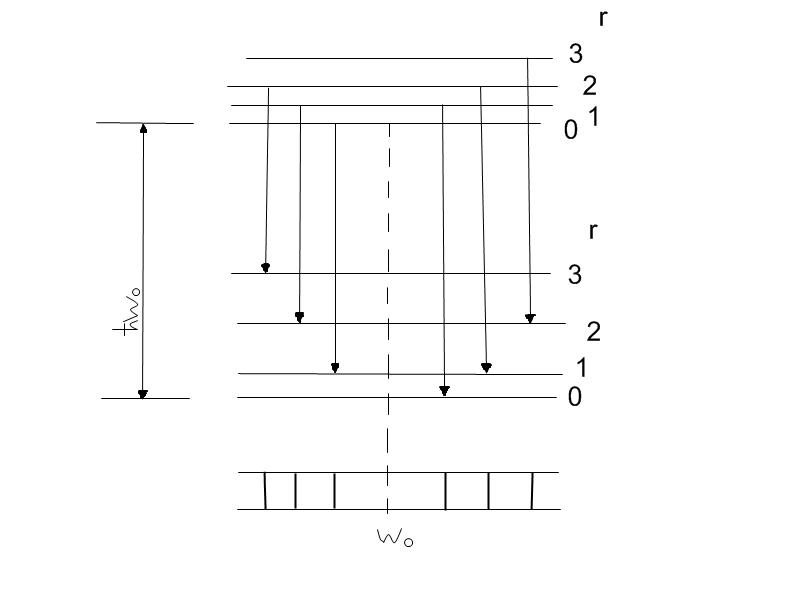 ∆Eкол
=
∆Eкол
=
∆Eвр>0 при r1>r2
∆Eвр<0 при r1<r2
Правило отбора разрешает переходы:
r1 = 3 → r2 = 2 => ∆Eвр = ∆E32
r1 = 2 → r2 = 1 => ∆Eвр = ∆E21
r1 = 1 → r2 =0 => ∆Eвр= ∆E10
r1 = 0 → r2 = 1 => ∆Eвр= -∆E10
r1 = 1 → r2 = 2 => ∆Eвр = -∆E21
r1 = 2 → r2= 3 => ∆Eвр = -∆E32
r1
= 0 → r2
= 0 запрещен, поэтому
 линии
с ω = ω0
в спектре нет.
линии
с ω = ω0
в спектре нет.
