Принцип суперпозиции

В волновой теории действует принцип суперпозиции волн. В квантовой теории ψ-функция формально обладает волновыми свойствами и постулативно принят принцип суперпозиции ψ-функций: если у некоторой системы возможными являются состояния 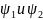, то для неё существует также состояние ,где - некоторые постоянные коэффициенты.

• Из можно получить и

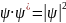
• Принцип суперпозиции подтверждается согласием с опытом вытекающих из него следствий.

Уравнение Шредингера

В 1926 г. Шредингер завершил поиск уравнения изменения состояния системы во времени: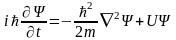 - общее уравнение Шредингера,

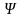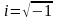где - волновая функция (комплексная функция координат и времени, формально обладающая волновыми свойствами и характеризующая волновые свойства частицы), , – оператор Лапласа, U – потенциальная энергия частицы.

Уравнение Шредингера:

1. есть новый фундаментальный закон, который введен постулативно;

2. справедливо, т.к. его следствия подтверждены экспериментально (Шредингер применил уравнение к атому водорода и получил для уровней энергии спектр, точно совпадающий с результатами опытов);

3. играет в квантовой физике такую же роль, как основное уравнение динамики в классической механике;

4. имеет особенность: в то время, как частица (в соответствии с интерпретацией Ψ – функции) «размазана» в пространстве, U рассматривается как потенциальная энергия точечной частицы в силовом поле.

Стационарные состояния

Стационарное состояние – состояние, в котором все наблюдаемые физические величины не зависят от времени.

Ψ – функция принципиально не наблюдаема и в стационарных состояниях она имеет вид: 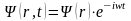, 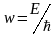–где Ψ(r) не зависит от времени. Тогда плотность вероятности 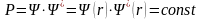, т.е. не зависит от t.

Подставим значение Ψ в стационарных состояниях в уравнение Шредингера:

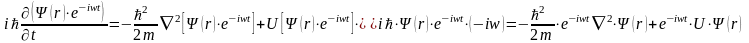
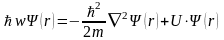или или

- уравнение Шредингера для стационарных состояний

U(r) определяется классически, как если бы волновыми свойствами частица не обладала.

Квантование

1)Решения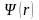 уравнения Шредингера имеют физический смысл, если удовлетворяют естественным (или стандартным) условиям: конечность;однозначность;непрерывность;

гладкость (без изломов).

2)Такие решения (собственные функции) возможны только при некоторых (собственных) значениях Е, которые принимают за возможные значения энергии в соответствующих стационарных состояниях, т.е. возникает квантование.

• В теории Бора квантование введено искусственно, в квантовой теории оно возникает естественно.

3)Эти значения Е могут быть дискретными или непрерывными, образуя дискретный или непрерывный энергетический спектр.

4)В общем случае ( ) уравнение Шредингера позволяет определить как распределение вероятности местоположения частицы, так и вероятности собственных значений ее энергии, импульса и момента импульса.

5)Уравнения Шредингера приводят к наличию строго стационарных состояний и с высокой точностью описывают поведение квантовых объектов.

Частица в прямоугольной яме

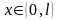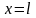Случай 1: частица находится в потенциальной яме (т.е. в связанном состоянии) с бесконечно высокими стенками и шириной l: при U = 0, при и U→ .

В пределах ямы 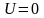и уравнение Шредингера: или ,

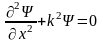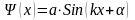где . Общее решение такого уравнения имеет вид: , где

а и - постоянные, причем 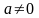(иначе частицы вообще нет).

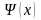конечна и однозначна. Вне ямы частица находиться не может, значит там 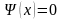. Из непрерывности следует, что 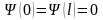. Тогда из .

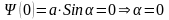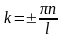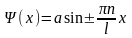Из и , где n = 1, 2, 3,… ( ,

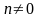иначе 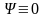и частицы вообще нет).

, откуда 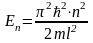, где n = 1, 2, 3, ..., т.е. энергия квантована и спектр ее дискретный. нормирована

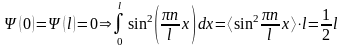
где n=1,2,3…

для n =1: низшее энергетическое состояние,

в середине ямы, по краям 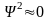, что резко отличается от классического поведения частицы. С ростом n и E_n максимумы 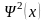располагаются все чаще и картина стремится стать равномерной, т.е. распределение стремится к классическому.

В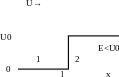 отличие от классической, у квантовой частицы , что хорошо согласуется с принципом неопределенности, т.к.

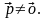
Случай 2 : Частица движется в одномерном потенциальном поле U(х).

1. Частица находится в потенциальной яме, полная энергия частицы

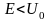
2. Классическая частица имеет непрерывный интервал

з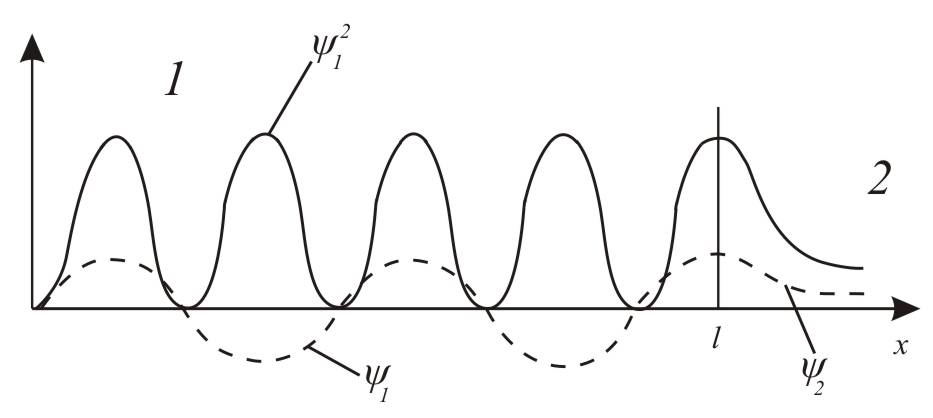 начений с равной вероятностью может быть обнаружена в любом месте ямы и за её пределы выйти не может (т.к. из следует, что при U = U₀ K< 0, что невозможно).

2. Квантовая частица, согласно расчетам при :

1. имеет дискретный спектр собственных значений Е, которому соответствуют связанные состояния и функции, характеризующие эти состояния. График одной из таких функций:

2. имеет функцию в области 2, т.е. (в противоречие классической физике) может быть там обнаружена. Такое возможно потому, что в квантовой теории равенство E = K + U теряет смысл: в силу принципа неопределенности K и U одновременно не могут принимать точные значения и в некоторых местах полная энергия E<U;

3. с ростом глубины ямы U₀число уровней энергии Е (и связанных состояний) растет, а вероятность 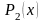обнаружения частицы в области 2 уменьшается. При U₀ и мы переходим к случаю 1.