17

Лекция 2. Теория автоматов.

Определение абстрактного автомата

Определение:

Абстрактный автомат - это модель преобразователя (устройства), которая характеризуется алфавитом входа, алфавитом выхода, алфавитом состояний, функцией выхода, функцией перехода: S=<Z,W,A,l,d> где Z = {z₁,z₂,...,z_m}- алфавит входа, W = {w₁,w₂,...,w_n} - алфавит выхода, A = {a₁,a₂,...,a_p} - алфавит состояний, l : A x Z -> W - функция выхода, d : A x Z -> A - функция перехода

    Предполагается, что автомат находиться всегда в некотором состоянии, и если это состояние a_i, то функция l определяет, какой выход будет иметь преобразователь, а d - какое у него будет новое состояние, если значение входа автомата равно w_j.

    Под алфавитом здесь понимается непустое множество попарно различных символов.

Способы задания автомата

    Чтобы задать конечный автомат S, необходимо описать все компоненты вектора S=<Z,W,A,l,d>, то есть входной и выходной алфавиты состояний, а также функции переходов и выходов.Среди множества состояний необходимо выделить состояние a₁, в котором автомат находится в момент времени t=0.

    Существуют несколько способов задания автомата, но наиболее часто используются табличный и графический.

1. Описание работы автомата  таблицами переходов и выходов иллюстрируется на следующем примере:

Функция перехода   d: A x Z -> A  

	a1	a2	..	ap
z1	a(1,1)	a(1,2)	..	a(1,p)
z2	a(2,1)	a(2,2)	..	a(2,p)
..	..	..	..	..
zm	a(m,1)	a(m,2)	..	a(m,p)

Функция выхода   l: A x Z -> W  

	a1	a2	..	ap
z1	w(1,1)	w(1,2)	..	w(1,p)
z2	w(2,1)	w(2,2)	..	w(2,p)
..	..	..	..	..
zm	w(m,1)	w(m,2)	..	w(m,p)

Строки этих таблиц соответствуют входным сигналам, а столбцы - состояниям, причем крайний левый столбец обозначен начальным состоянием a₁. На пересечении столбца i и строки j в таблице переходов ставится состояние (i,z_j)=a_s, в которое автомат переходит из состояния a_i под действием сигнала z_j,а в таблице выхода - соответствующий этому переходу выходной сигнал w(i,j)=l(a_i,z_j)=w_r.

2. Для описания работы автомата можно использовать объединенную таблицу:

Функции перехода и выхода

	a1	a2	..	ap
z1	a1,1/w1,1	a1,2/w1,2	..	a1,p/w1,p
z2	a2,1/w2,1	a2,2/w2,2	..	a2,p/w2,p
..	..	..	..	..
zm	am,1/wm,1	am,2/wm2,2	..	am,p/wm,p

a(i,j)=d(a_i,z_j)=a_s ; w(i,j)=l(a_i,z_j)=w_r  

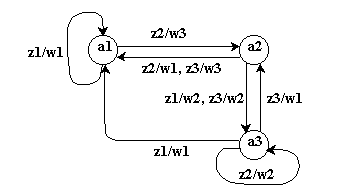
2. Определение: Граф автомата - ориентированный граф, вершины крторого соответствуют состояниям, а дуги - переходам между ними, например: