
- •Определение передаточной функции объекта регулирования по экспериментальной переходной функции методом «площадей»
- •Исходные данные
- •Оценка точности аппроксимации
- •Определение передаточной функции графическим методом
- •Определение передаточной функции объекта регулирования из дифференциального уравнения процесса
- •2.Расчет оптимальных настроек в одноконтурных системах с линейными законами регулирования
![]()
Определение передаточной функции объекта регулирования по экспериментальной переходной функции методом «площадей»
Построение математической модели линейной системы по экспериментальной переходной функции производится в следующем порядке:
на основании формы переходной функции и в зависимости от физических свойств исследуемой системы устанавливается вид передаточной функции модели;
определяются значения коэффициентов передаточной функции на условия наилучшего приближения модели объекта;
производится оценка точности аппроксимации.
Одним из наиболее простых и удобных для счета на ЦВМ методов аппроксимации переходных процессов является метод «площадей» (программа 1)
Рассмотрим функцию h(t),
которая получена из экспериментальной
переходной функции объекта путём
исключения чистого запаздывания
![]() и нормировки. Пусть h(o)=
и нормировки. Пусть h(o)=![]() (o)=0
(o)=0
При аппроксимации функции h(t) на практике обычно задаются следующими структурами передаточной функции модели:
![]() (1.1)
(1.1)
![]() (1.2)
(1.2)
![]() ; (1.3)
; (1.3)
Выражение
![]() ,
обратное передаточной функции модели,
можно разложить в ряд по степеням P
,
обратное передаточной функции модели,
можно разложить в ряд по степеням P
=![]() (1.4)
(1.4)
Очевидно, что для модели
1)![]()
![]()
![]()
для модели (1.2)
для модели (1.3) коэффициенты
![]() ,
I = 1, 2, 3 связаны с
коэффициентами
,
I = 1, 2, 3 связаны с
коэффициентами
![]() разложения (1.4) системой уравнений
разложения (1.4) системой уравнений
![]() ,
, ![]() , (1.5)
, (1.5)
![]() ,
0=
,
0=![]() .
.
Для определения
![]() воспользуемся связью между S
и некоторыми функциями от (1-h).
Величину L(1-h)
можно представить так:
воспользуемся связью между S
и некоторыми функциями от (1-h).
Величину L(1-h)
можно представить так:
![]() .
.
Отсюда ![]() ,
,
или 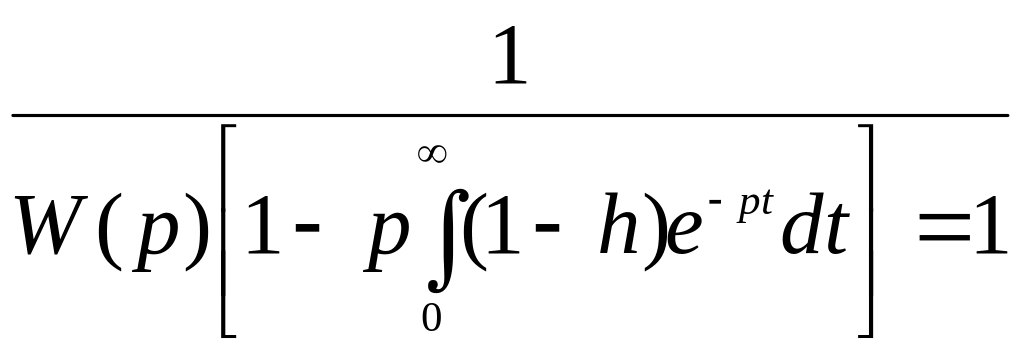 .
1.6
.
1.6
Разложим функцию![]() в ряд по степеням pt
в ряд по степеням pt
![]()
![]() 1.7
1.7
![]()
![]()
![]()
![]() (1.8)
(1.8)
Из выражения (1.8) следует, что цоэффициенты Si связаны с переходной функцией h(t) соотношениями:
![]()
![]()
![]()
![]()
Моментом i-го порядка функции 1-h(t) называется несобственный интеграл:
![]() (1.9)
(1.9)
тогда формулу можно преобразовать:
![]()
![]()
![]() ,
,
![]() (1.10)
(1.10)
Таким образом, определив по графику h(t) значения Mi методом численного интегрирования [I] и вычислив из соотношений величины «площадей» Si, нетрудно найти значение коэффициентов передаточной функции моделей (1.1)+(1.3).
Выбор вида передаточной функции модели производится из следующих соображений: если коэффициенты S1,S2,S3 положительны, то в зависимости от вида функции h(t) задаются моделью (1.1) или (1.2). Если хоть один из них отрицателен, задаются моделью (1.3).
Перед обращением к программе из экспериментальной кривой разгона необходимо выделить время чистого запаздывания ϊ, затем провести дискретизацию по времени с шагом ∆t и нормировку. Шаг квантования по времени выбирается таким, чтобы на интервале между двумя соседними отсчетами переходная функция была близка к прямой.
Приведение кривой разгона к нормированному, то есть безразмерному виду осуществлиется с помощью формулы
![]() .
(1.11)
.
(1.11)
Пример.
Рассчитать и исследовать систему автоматического регулирования температуры пароагрегатной смеси (ПАС), рис 1.1.

Исходные данные
Канал регулирующего воздействия изменения задачи регулятору на °С- кривая разгона объекта
t,мин |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
5 |
0°С |
38 |
38,2 |
38,4 |
38,6 |
38,9 |
39,3 |
40 |
40,5 |
40,9 |
4,5 |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
41,2 |
41,5 |
41,8 |
41,9 |
41,9 |
42 |
42 |
Канал возмущающего воздействия (изменение расхода сырья на 20% хода регулирующего органа) – передаточная функция объекта в виде апериодического звена 1 порядка
![]()
к=0,2°С/% хода р.о. Т=1,7 мин.
Проведем нормировку кривой разгона. Дискретизацию по времени выберем ∆t=5. Нормированная переходная функция приведена на рис. 1.2.
После обращения к СП вычисления цоэффициентов передаточной функции методом «площадей», на основании полученных результатов зададимся моделью (1.2), т.е. окончательно
![]()
