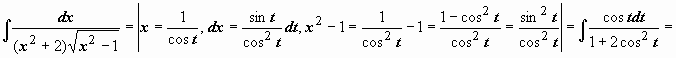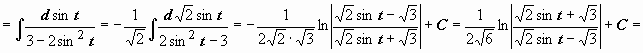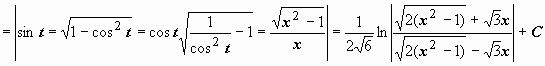- •10.1. Первообразная функция.
- •Если функция
- •10.2. Неопределённый интеграл и его свойства.
- •10.3. Таблица неопределённых интегралов.
- •10.4. Простейшие правила интегрирования.
- •10.5. Замена переменной в неопределённом интеграле (интегрирование подстановкой).
- •10.6. Интегрирование по частям.
- •10.7. Интегралы, содержащие квадратный трёхчлен .
- •10.8. Интегрирование рациональных функций.
- •10.9. Интегрирование функций, рационально зависящих от .
- •10.9.2. Частные тригонометрические подстановки.
- •10.10. Интегрирование некоторых алгебраических иррациональностей.
10.9. Интегрирование функций, рационально зависящих от .
В
этом разделе мы рассмотрим интегралы
![]() ,
где рационально зависящая от sin x,
cos x
функция R(sin
x,
cos x)
- отношение двух многочленов относительно
этих функций (пример -
,
где рационально зависящая от sin x,
cos x
функция R(sin
x,
cos x)
- отношение двух многочленов относительно
этих функций (пример -
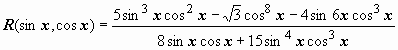 ).
10.9.1.
Универсальная тригонометрическая
подстановка.
Переход в подынтегральной функции к
переменной
).
10.9.1.
Универсальная тригонометрическая
подстановка.
Переход в подынтегральной функции к
переменной
![]() преобразует
R(sin
x,
cos x)
в функцию, рационально зависящую от t;
методы интегрирования таких функций
рассмотрены в предыдущем разделе.
Выразим sin x,
cos x,
dx
через t:
преобразует
R(sin
x,
cos x)
в функцию, рационально зависящую от t;
методы интегрирования таких функций
рассмотрены в предыдущем разделе.
Выразим sin x,
cos x,
dx
через t:
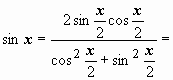 (делим
на
(делим
на
![]() )
)
![]() ;
;
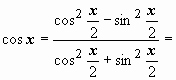 (делим
на
)
(делим
на
)
![]() .
В результате все компоненты подынтегральной
функции выражаются через функции,
рационально зависящие от t.
Пример:
.
В результате все компоненты подынтегральной
функции выражаются через функции,
рационально зависящие от t.
Пример:
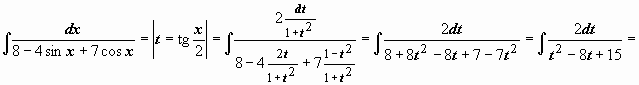
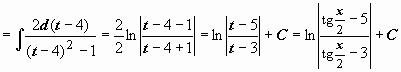 .
Универсальная
тригонометрическая подстановка всегда
рационализирует подынтегральную
функцию, с её помощью легко берутся
интегралы вида
.
Универсальная
тригонометрическая подстановка всегда
рационализирует подынтегральную
функцию, с её помощью легко берутся
интегралы вида
![]() (a,
b,
c
- постоянные); однако часто она приводит
к очень громоздким рациональным дробям,
у которых, в частности, практически
невозможно найти корни знаменателя.
Поэтому при возможности применяются
частные подстановки, которые тоже
рационализируют подынтегральную функцию
и приводят к менее сложным дробям.
(a,
b,
c
- постоянные); однако часто она приводит
к очень громоздким рациональным дробям,
у которых, в частности, практически
невозможно найти корни знаменателя.
Поэтому при возможности применяются
частные подстановки, которые тоже
рационализируют подынтегральную функцию
и приводят к менее сложным дробям.
10.9.2. Частные тригонометрические подстановки.
10.9.2.1.
Подынтегральная функция нечётна
относительно sin
x,
т.е. R(-sin
x,
cos x)
== -
R(sin
x,
cos x).
В этом случае применима подстановка t
= cos x.
10.9.2.2.
Подынтегральная функция нечётна
относительно cos
x,
т.е. R(sin
x,
-cos x)
= = -
R(sin
x,
cos x).
В этом случае применима подстановка t
= sin x.
10.9.2.3.
Подынтегральная функция чётна относительно
sin
x
и cos x,
т.е. R(-sin
x,
-cos x)
= R(sin
x,
cos x).
В этом случае применима подстановка t
= tg x
(или t
= ctg x,
причём ответить на вопрос, что лучше,
может только проба). Выражения
sin
x,
cos x
и dx
через tg x:
![]() .
Примеры:
1.
.
Примеры:
1.
![]() .
Подынтегральная функция нечётна
относительно sin x:
.
Подынтегральная функция нечётна
относительно sin x:
![]() ,
поэтому
,
поэтому
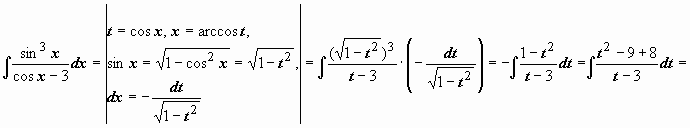
![]() .
(можно перейти к
.
(можно перейти к
![]() более
просто:
более
просто:
![]() и
т.д.)
2.
и
т.д.)
2.
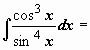 (Подынтегральная
функция нечётна относительно
cos
x)
=
(Подынтегральная
функция нечётна относительно
cos
x)
=
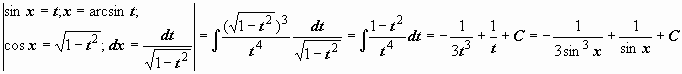 .
3.
.
3.
![]() (подынтегральная
функция не меняется при одновременном
изменении знака у sin x
и cos x,
поэтому t
= tg x)
(подынтегральная
функция не меняется при одновременном
изменении знака у sin x
и cos x,
поэтому t
= tg x)
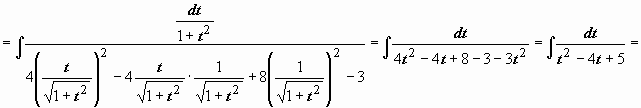
![]() .
При
нахождении таких интегралов для понижения
степеней иногда целесообразно
воспользоваться основным тригонометрическим
тождеством:
.
При
нахождении таких интегралов для понижения
степеней иногда целесообразно
воспользоваться основным тригонометрическим
тождеством:
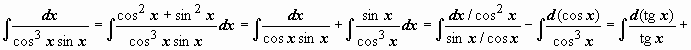
![]() .
Интегрирование
степеней
tg x
и ctg x
попадает под пункт 10.9.2.3:
.
Интегрирование
степеней
tg x
и ctg x
попадает под пункт 10.9.2.3:
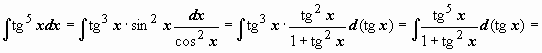
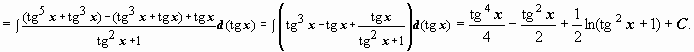
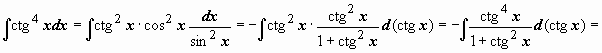
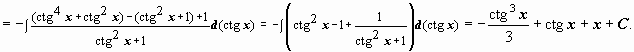 10.9.3.
Интегрирование произведения чётных
степеней sin
x,
cos x.
При вычислении интегралов
10.9.3.
Интегрирование произведения чётных
степеней sin
x,
cos x.
При вычислении интегралов
![]() следует
понизить степень тригонометрических
функций переходом к косинусу двойного
угла:
следует
понизить степень тригонометрических
функций переходом к косинусу двойного
угла:
![]() .
Угол удваивается до тех пор, пока одна
из степеней не станет нечётной, после
этого можно воспользоваться приёмами
10.9.2.1
или 10.9.2.2.
Пример:
.
Угол удваивается до тех пор, пока одна
из степеней не станет нечётной, после
этого можно воспользоваться приёмами
10.9.2.1
или 10.9.2.2.
Пример:
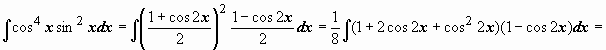
![]()
![]()
![]() .
10.9.4.
Интегрирование произведений синусов
и косинусов кратных дуг.
При нахождении интегралов вида
.
10.9.4.
Интегрирование произведений синусов
и косинусов кратных дуг.
При нахождении интегралов вида
![]() ,
,
![]() ,
,
![]() с
помощью школьных тригонометрических
формул
с
помощью школьных тригонометрических
формул
![]() ,
,
![]() ,
,
![]() задача
сводится к интегрированию линейной
комбинации тех же функций (с другими
аргументами). Пример:
задача
сводится к интегрированию линейной
комбинации тех же функций (с другими
аргументами). Пример:
![]()
![]() .
.
10.10. Интегрирование некоторых алгебраических иррациональностей.
10.10.1.
Интегралы вида
![]() ,
где
,
где
![]() -
натуральное число,
-
натуральное число,
![]() -
функция, рационально зависящая от своих
аргументов.
Пример
такой функции -
-
функция, рационально зависящая от своих
аргументов.
Пример
такой функции -
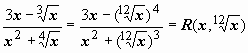 .
Как видно из этого примера, к рассматриваемому
типу сводятся интегралы вида
.
Как видно из этого примера, к рассматриваемому
типу сводятся интегралы вида
![]() ,
где p,
q,
r,
… - рациональные числа, так как, если n
- общий знаменатель чисел p,
q,
r,
… , то подынтегральная функция рационально
зависит от x
и
,
где p,
q,
r,
… - рациональные числа, так как, если n
- общий знаменатель чисел p,
q,
r,
… , то подынтегральная функция рационально
зависит от x
и
![]() .
Подстановка x
= t
n
рационализирует подынтегральную
функцию, т.е. сводит её к рациональной
функции переменной t.
Пример:
.
Подстановка x
= t
n
рационализирует подынтегральную
функцию, т.е. сводит её к рациональной
функции переменной t.
Пример:
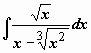 .
Наименьшее общее кратное показателей
корней равно 6, поэтому применяем
подстановку x
= t
6:
.
Наименьшее общее кратное показателей
корней равно 6, поэтому применяем
подстановку x
= t
6:
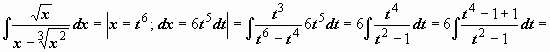
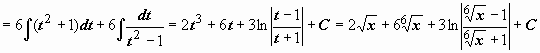 .
10.10.2.
Интегралы вида
.
10.10.2.
Интегралы вида
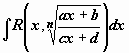 ,
где a,
b,
c,
d
- постоянные, остальные параметры имеют
тот же смысл, что и в предыдущем разделе,
рационализируются подстановкой
,
где a,
b,
c,
d
- постоянные, остальные параметры имеют
тот же смысл, что и в предыдущем разделе,
рационализируются подстановкой
![]() .
Пример:
.
Пример:
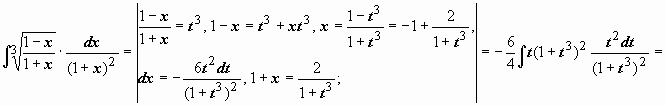
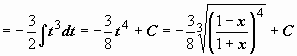 .
10.10.3.
Тригонометрические подстановки для
интегралов вида
.
10.10.3.
Тригонометрические подстановки для
интегралов вида
![]() .
В
разделе 10.7.
Интегралы, содержащие квадратный
трёхчлен,
мы уже рассматривали некоторые методы
интегрирования таких функций. Здесь мы
рассмотрим тригонометрические подстановки
для вычисления таких интегралов, которые
сводят подынтегральнуюфункцию к функции,
рационально зависящей от
.
В
разделе 10.7.
Интегралы, содержащие квадратный
трёхчлен,
мы уже рассматривали некоторые методы
интегрирования таких функций. Здесь мы
рассмотрим тригонометрические подстановки
для вычисления таких интегралов, которые
сводят подынтегральнуюфункцию к функции,
рационально зависящей от
![]() и
и
![]() .
После выделения полного квадрата в
трёхчлене (и соответствующей линейной
замены переменной) интеграл сводится,
в зависимости от знаков
и
дискриминанта трёхчлена, к интегралу
одного из следующих трёх видов:
.
После выделения полного квадрата в
трёхчлене (и соответствующей линейной
замены переменной) интеграл сводится,
в зависимости от знаков
и
дискриминанта трёхчлена, к интегралу
одного из следующих трёх видов:
![]() ,
,
![]() ,
,
![]() .
Далее:
.
Далее:
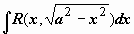 рационализируется
подстановкой x
= a
sin
t
(или x
= a
cos
t).
Мы применяли эту подстановку в разделе
10.5.
Замена переменной в неопределённом
интеграле.
рационализируется
подстановкой x
= a
sin
t
(или x
= a
cos
t).
Мы применяли эту подстановку в разделе
10.5.
Замена переменной в неопределённом
интеграле.рационализируется подстановкой
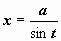 (или
(или
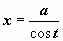 ,
или
,
или
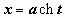 ).
).
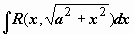 рационализируется
подстановкой x
= a
tg
t
(или x
= a
ctg
t,
или
рационализируется
подстановкой x
= a
tg
t
(или x
= a
ctg
t,
или
x = a sh t).
Примеры:
1.
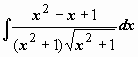 .
Интеграл вида
,
из возможных подстановок наиболее
удобной оказывается x
= ctg t
( это можно установить только пробой!).
.
Интеграл вида
,
из возможных подстановок наиболее
удобной оказывается x
= ctg t
( это можно установить только пробой!).
![]() ,
поэтому
,
поэтому
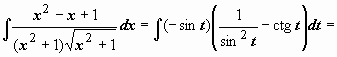
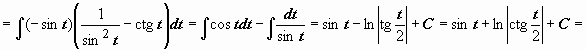
![]() .
Ответ можно записать поизящнее. По
школьным формулам
.
Ответ можно записать поизящнее. По
школьным формулам
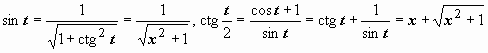 ,
поэтому
,
поэтому
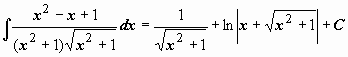 .
2.
.
2.