§3. Раскрытие неопределенностей вида Пример 1.
Вычислить предел
функции
.
Решение. Знаменатель
дроби
обращается в нуль при
,
а потому функция
при
не существует. Теорему о пределе дроби
применить нельзя, так как предел
знаменателя равен нулю. Но определение
предела функции содержит существенную
оговорку: при отыскании предела функции
при
значение функции
при
может не рассматриваться.
Т.к. при
числитель и знаменатель дроби –
бесконечно малые функции
и
,
то имеем неопределенность вида
.
Для решения задачи
используем правило 2.1 (см. таблицу).
Разделим числитель и знаменатель на
.
Мы имеем право это сделать, потому что
значение
не рассматривается, и, значит
.
.
Ответ:
.
Пример 2.
Вычислить предел
функции
.
Решение. Имеем
неопределенность
.
По правилу 2.1 разделим числитель и
знаменатель на
.
0
Тогда
.
Еще раз разделим числитель и знаменатель на :
.
Ответ:
Пример 3.
Вычислить предел
функции
.
Решение.
Имеем неопределенность
.
По правилу 2.2 умножим числитель и
знаменатель на выражение, сопряженное
числителю и применим формулу
:
Ответ:
.
Пример 4.
Вычислить предел
функции
.
Решение.
Т.к. здесь неопределенность
и знаменатель содержит иррациональность,
то, используя правило 2.2, умножим числитель
и знаменатель дроби на неполный квадрат
(т.к. корень кубический) и применим
формулу
.
Имеем
Ответ:
.
Пример 5.
Вычислить предел
.
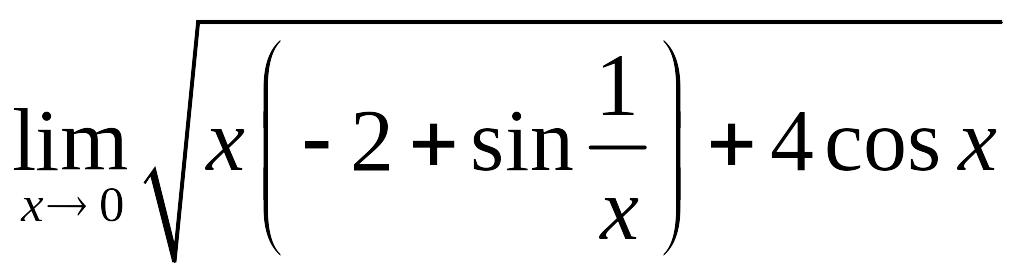Решение.
Т.к функция у=
непрерывна при всех x,то,
переходя к пределу под знаком непрерывной
функции, получаем
.
Т.к x – бесконечно малая функция в точке x=0,
а функция
-ограниченная
в окрестности точки x = 0,
то
-бесконечно
малая функция в точке x = 0
(произведение бесконечно малой функции
на ограниченную функцию – есть бесконечно
малая функция), т.е.
.
Т.к. функция
непрерывна в точке x = 0,
то
.
Используя основные теоремы о пределе функции в точке, получим
.
Ответ:
.
§4. Первый замечательный предел
Пример 1.
Вычислить предел
функции
.
Решение.
Выражение под знаком предела является отношением двух бесконечно малых величин, имеем неопределенность вида .Учитывая, что
,
имеем,
.
Воспользуемся по
правилу 4.1 первым замечательным пределом
.
Для этого умножим и числитель, и
знаменатель на
:
=4
.
Ответ:
.
Пример 2.
Вычислить предел
.
Решение.
Имеем неопределенность вида .
Сделаем замену переменной
,
при
,
и воспользуемся формулами тригонометрии
.
Заменим бесконечно малые функции эквивалентными при :
~
,
~
,
~
,
тогда
.
Ответ:
.
§5. Второй замечательный предел
Пример 1.
Вычислить предел
функции
.
Решение.
.
Преобразуем выражение под знаком предела так, чтобы можно было использовать второй замечательный предел, правило 4.2,
.
При
.
Сформируем степень,
учтем, что
и
.
Получим,
е
=е
=
=
=-5.
Ответ:
.
Пример 2.
Вычислить предел числовой последовательности
.
Решение.
При
выражение под знаком предела представляет
собой степень, основание которой
стремится к единице:
,
а показатель к бесконечности
.
Таким образом, мы имеем дело с неопределенностью вида .
Преобразуем выражение
под знаком предела так, чтобы по правилу
4.2 использовать второй замечательный
предел
е:
(т.к.
при
то
).
Ответ:
.
Пример 3.
Вычислить предел
функции
.
Решение.
Поскольку
и
=0,то
выражение под знаком предела является
отношением двух бесконечно малых функций
при x
1
(неопределенность вида
).
Воспользуемся правилом 4.2.
Сделаем замену переменной
,
(где
- одна из форм второго замечательного
предела)
Ответ:
.
Пример 4.
Вычислить предел
функции
.
Решение.
Здесь имеет место неопределенность .
Воспользуемся свойствами логарифмов
и
,
а также вторым замечательным пределом, правило 4.2:
Ответ:
.
§6. Одновременное использование первого и второго замечательных пределов
Пример 1.
Вычислить предел
функции
.
Решение.
Имеем неопределенность .
Воспользовавшись
правилом 4.2, умножим числитель и
знаменатель на
.
При
,
поэтому воспользуемся одной из форм
второго замечательного предела
.
.
Использовали правило
4.1. При
,
.
Ответ:
.
Пример 2.
Вычислить предел
функции
.
Решение.
Имеем неопределенность . В числителе добавим и вычтем 1:
.
Затем поделим числитель
и знаменатель дроби на
и воспользуемся свойствами пределов,
первым замечательным пределом
(правило 4.1) и одной из форм второго
замечательного предела:
(правило 4.2).
.
Ответ:
.
Варианты контрольных заданий