Определенный интеграл

10 Задачи, приводящие к понятию определенного интеграла

10.1) Задача о площади криволинейной трапеции.

Опред. Криволинейной трапециец называют фигуру, ограниченную графиком непрерывной функции y=f(x) (f(x)=0), осью 0х и прямыми х=а, х=b

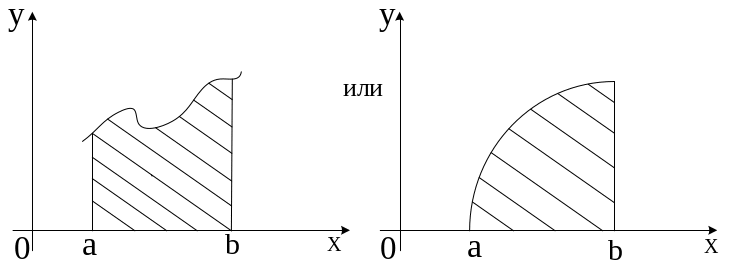
Вычислим площадь такой фигуры

Заметим, что:

1) площадь есть неотрицательное число;

2) равные фигуры имеют равные площади;

3) площадь всей фигуры равна сумме площадей частей, на которые разбита эта фигура.

Для решения этой задачи разобьем отрезок [a, b] произвольным способом на n малых отрезков точками

х₀ = а, х₁, х₂, …, х_n = b

Обозначим длины этих отрезков через

…,

Обозначим через m_к и М_к через наименьшее и наибольшее значения функции f(x) на к-ом элементарном отрезке [х_к-1, х_к].

Построим на каждом элементарном отрезке, как на основании, два элементарных прямоугольника: «входящий» с высотой m_к и «выходящий» с высотой М_к. Их площади будут соответственно равными и .

- сумма площадей всех «входящих» прямоугольников, т. е. площадь вписанной ступенчатой фигуры (рис. 1)

- сумма площадей всех «выходящих» прямоугольников, т. е. площадь описанной ступенчатой фигуры (рис. 2)

S – площадь криволинейной трапеции

При любом разбиении отрезка [a, b] имеем следующее двойное неравенство:

(1)

Для любого числа n S_n и S_n – будут определены, т. е. известны. А S – мы должны будем определить.

Построим теперь на элементарных отрезках [х_к-1, х_к] прямоугольники третьего вида: высота каждого прямоугольника равна ,

где х_к-1 х_к,

а значит m_к М_к

Площадь такого прямоугольника равна .

Площадь фигуры, составленной из таких прямоугольников

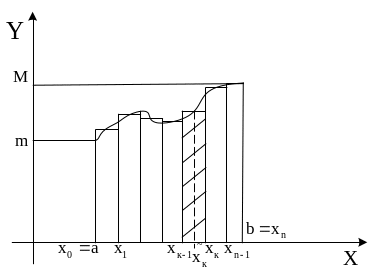
Сама эта фигура (рис. 3), есть ступенчатая фигура, занимающая некоторое промежуточное положение между фигурами, состоящими из всех «входящих» прямоугольников (рис. 1) и всех «выходящих» прямоугольников (рис. 2)

(2)

или кратко

Это неравенство справедливо при всяком n и любом способе разбиения отрезка [a, b] и при любом выборе точки в элементарных отрезках. Из рисунка 3 видим, что

> и <

C увеличением числа n, -- уменьшается, величина - монотонно возрастает, оставаясь < ,

величина - монотонно убывает, оставаясь >

Это значит, что существуют пределы и при (свойство пределов)

Из равенства (2) следует, что (свойство пределов)

Но А = S – площадь криволинейной трапеции.

Следовательно

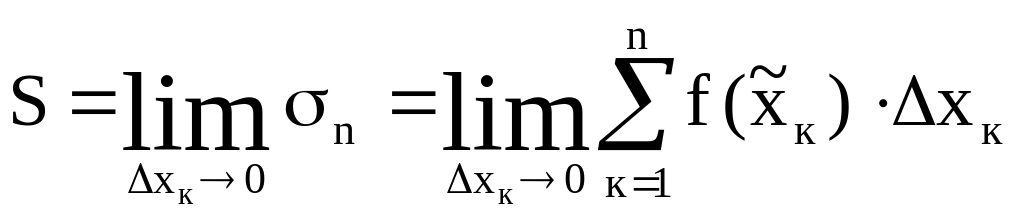
Площадь криволинейной трапеции называется предел, к которому стремится площадь ступенчатой фигуры (рис. 3), составленной из элементарных прямоугольников, когда .

10.2) Задача о работе переменной силы.

Пусть под действием некоторой силы F материальная точка М движется по прямой OS, причём, направление силы совпадает с направлением движения. Требуется найти работу, произведённую силой F при перемещении точки М из положения s = a в положение s = b.

1) если сила F=const, то A=F(b-a). Работа равна произведению силы на длину пути.

2) Предположим, что сила F непрерывно меняется в зависимости от положения материальной точки, т.е. представляет собой функцию F(s), непрерывную на отрезке [a,b]. Разобьём отрезок [a,b] на n произвольных частей с длинами . На каждом частичном отрезке выберем произвольную точку

Предполагая, что сила на каждом элементарном отрезке сохраняет постоянное значение равное, , найдём работу на пути ,

а будет приближённое значение выражение работы силы F на всём отрезке [a,b]. Предел этой суммы при и выражает работу силы F(s) на пути от точки S = a до точки S = b.

.