
- •Часть 2
- •Часть 2
- •Оглавление
- •4.1. Основные сведения 12
- •5.1. Основные сведения 22
- •Введение
- •Лабораторная работа 3
- •На устойчивость систем
- •3.1. Основные сведения
- •3.2. Порядок выполнения работы
- •3.3. Контрольные вопросы
- •Лабораторная работа 4 точность систем и методы ее повышения
- •4.1. Основные сведения
- •4.2. Порядок выполнения работы
- •4.3. Контрольные вопросы
- •Лабораторная работа 5 качество процессов управления и методы его обеспечения
- •5.1. Основные сведения
- •5.2. Порядок выполнения работы
- •5.3. Контрольные вопросы
- •Библиографический список
- •Часть 2
- •644046, Г. Омск, пр. Маркса, 35
5.2. Порядок выполнения работы
1
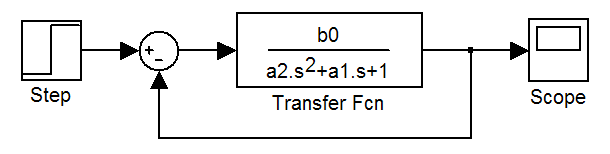 Рис.
5.4. Модель замкнутой
исходной системы
Рис.
5.4. Модель замкнутой
исходной системы
2.
Выберите параметры объекта
![]() также как в п.2 лабораторной работы 4.
Промоделируйте систему и получите
переходный процесс, определите показатели
качества
также как в п.2 лабораторной работы 4.
Промоделируйте систему и получите
переходный процесс, определите показатели
качества
![]() .
.
Получите
логарифмические характеристики (система
должна быть разомкнута), определите
показатели устойчивости
и
![]() .
.
3. Сравните полученные показатели качества и устойчивости с данными табл. 1 и занесите их в табл. 2 для исходной системы.
4) Для исследования системы с ПИД-регулятором соберите соответствующую имитационную модель, приведенную на рис. 5.5.
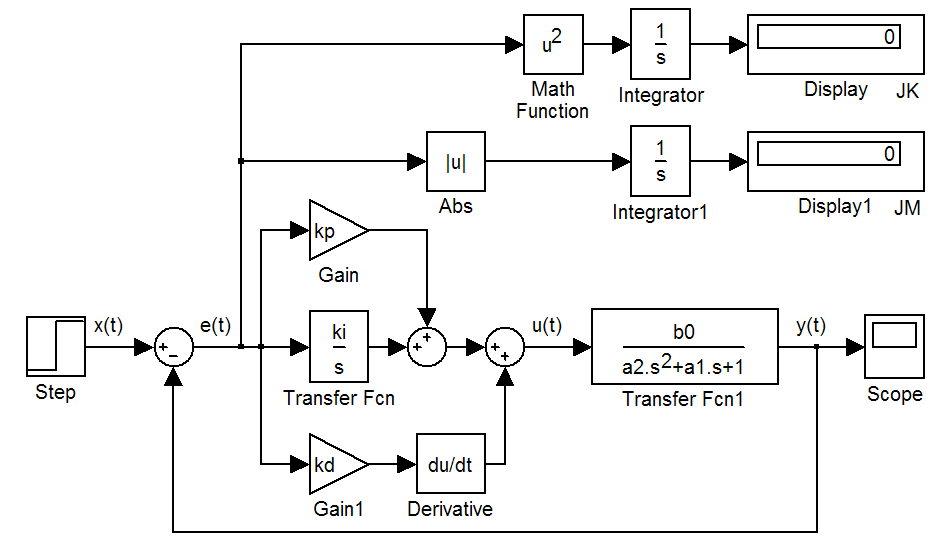 Рис.
5.5. Схема имитационного моделирования
системы с ПИД-регулятором
Рис.
5.5. Схема имитационного моделирования
системы с ПИД-регулятором
Математические
блоки Abs (изображение
![]() )
и (
)
и (![]() )
осуществляют операции вычисления модуля
и квадрата, которые используются в
интегральных оценках (5.13) и (5.14). Для
отображения результатов используется
блок Display.
)
осуществляют операции вычисления модуля
и квадрата, которые используются в
интегральных оценках (5.13) и (5.14). Для
отображения результатов используется
блок Display.
5.
Задайте числовые значения параметров
![]() ,
полученные в лабораторной работе 4 для
ПИ-регулятора.
,
полученные в лабораторной работе 4 для
ПИ-регулятора.
6. Изменяя
значение
,
получите экспериментальную зависимость
установившихся значений интегральных
оценок JK и JM
от
.
Определите
![]() минимизирующий JK и
минимизирующий JK и
![]() –
соответственно JM.
–
соответственно JM.
7.
Промоделируйте систему при
![]() и
и
![]() ,
получите графики переходных процессов
и логарифмические характеристики.
Определите показатели качества и
устойчивости для каждого из коэффициентов
.
,
получите графики переходных процессов
и логарифмические характеристики.
Определите показатели качества и
устойчивости для каждого из коэффициентов
.
8. По полученным показателям обоснуйте выбор параметра и соответствующие ему показатели занесите в табл. 2 для ПИД-регулятора.
9. Для исследования системы с компенсационным регулятором (КР) по данным табл. 2 определите минимальное время регулирования .
Выберите
из диапазона
![]() постоянную времени
постоянную времени
![]() ,
вычислите по формулам (5.34) параметры
ПИД-регулятора и запишите их.
,
вычислите по формулам (5.34) параметры
ПИД-регулятора и запишите их.
10.
Полученные в п.9 значения
![]() задайте в схеме имитационного моделирования
на рис. 5.5.
задайте в схеме имитационного моделирования
на рис. 5.5.
11. Промоделируйте
систему и значения параметров качества
![]() и
устойчивости
и
устойчивости
![]() занесите в табл. 2. Поместите в отчет
графики h(t)
и логарифмических характеристик.
занесите в табл. 2. Поместите в отчет
графики h(t)
и логарифмических характеристик.
12. Для исследования возможностей системы с минимально-фазовой коррекцией (МФК), соберите схему моделирования в соответствии с рис. 5.6.
 Рис.
5.6. Схема моделирования системы с
корректирующим устройством
Рис.
5.6. Схема моделирования системы с
корректирующим устройством
13.
Задайте параметр
![]() интегрирующего звена в соответствии с
п. 5.
интегрирующего звена в соответствии с
п. 5.
14.
Промоделируйте систему, получите
логарифмические характеристики и
определите частоту среза
![]() .
.
15.
Выберите постоянные времени T1
и T2
корректирующего устройства так,
чтобы для соответствующих частот
сопряжения
![]() и
и
![]() выполнялось неравенство
выполнялось неравенство
![]() . (5.35)
. (5.35)
16. Выбором параметров T1 и T2 получите систему с максимально возможным запасом по фазе. Получите логарифмические характеристики, запасы устойчивости и поместите в табл. 2.
17. Соберите схему имитационного моделирования переходных процессов по аналогии с рис. 5.5.
18.
Промоделируйте систему, получите h(t),
определите значения показателей качества
![]() ,
интегральных оценок JM,
JK. Занесите их в
табл. 2.
,
интегральных оценок JM,
JK. Занесите их в
табл. 2.
Таблица 2
Результаты моделирования системы с исследуемыми параметрами
Показатели качества и устойчивости |
Исходная система |
Скорректированная система |
||
ПИД |
МФК |
КР |
||
Время регулирования
|
|
|
|
|
Перерегулирование , % |
|
|
|
|
Колебательность, m |
|
|
|
|
Интегральная оценка JM |
|
|
|
|
Интегральная оценка JK |
|
|
|
|
Запас устойчивости по фазе
|
|
|
|
|
Запас устойчивости по амплитуде , дБ |
|
|
|
|
19. Проанализируйте результаты моделирования табл. 2 и сделайте вывод о качестве и устойчивости процессов управления в замкнутых системах с исследуемыми регуляторами.
20. Выберите наиболее предпочтительный вид регулятора и метода определения параметров.
