Описание установки

В работе используется мост Уитстона, в плечи которого включены магазины сопротивлений R₁, R₂, R₃ и искомый резистор R_x. Источником питания служит батарея аккумуляторов или выпрямитель ВС 4-12, включаемый в электрическую сеть через РНШ.

Выполнение работы.

1. Собрать цепь по схеме рис. 3. Сопротивление в магазинах R₂ и R₃ установить равными между собой (R₂ = R₃) по заданию преподавателя (10…20 Ом.). Сопротивление магазина R₂ и R₁ следует установить близким по значению с сопротивлением измеряемого резистора (5…10 Ом).

2. Чувствительность моста Уитстона в большой степени зависит от величины напряжения источника питания. Поэтому для удобства измерений рекомендуется использовать выпрямитель ВС 4-12, включаемый через автотрансформатор РНШ.

3. Замкнув ключ S при помощи автотрансформатора, плавно прибавляют напряжение до тех пор, пока стрелка гальванометра в диагонали моста заметно не отклонится от нуля.

4. Подбирая значение сопротивления в магазине R₁, добиваются отсутствия тока в диагонали моста – стрелка гальванометра на нуле! При этом условии вычисляют R_x.

5. Повторить измерение R_x при других значениях R₂, R₃.

6. Аналогичные измерения провести для другого резистора R_x1 и для их последовательного соединения.

7. Результаты измерений и вычислений занести в таблицу.

Измеряемый резистор	№№ п.п.	Измерено			Вычислено
		R1, Ом	R2, Ом	R3, Ом	Rx, Ом	Rx, Ом	Rxср, Ом	Е, %
Rx	1. 2. 3.
Rx1	1. 2. 3.
Rx + Rx1	1. 2. 3.

8. Ошибки R_x вычисляют дифференциальным способом. Абсолютные погрешности результатов прямых измерений R₁, R₂, R₃ определяются по основной погрешности магазина

,

где R – номинальное значение установленного в магазине сопротивления;

 – класс точности магазина сопротивлений;

m – число декад в магазине;

a = 0,005 –1- постоянная данного магазина.

Контрольные вопросы

1. Сформулируйте и обоснуйте правила Кирхгофа.

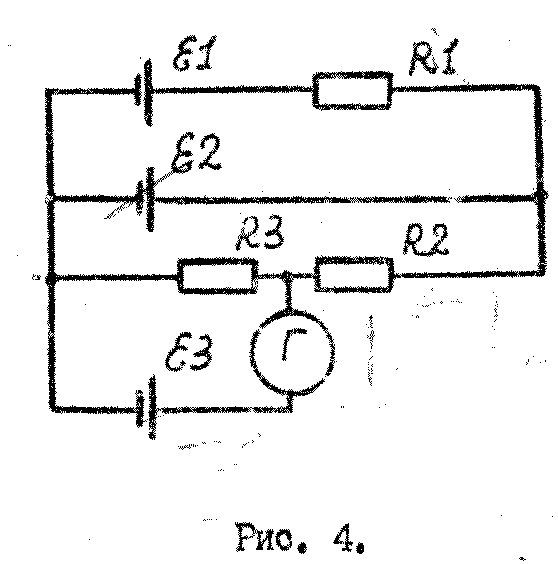
2. Считая известными ₁, ₂, R₁, R₂, R₃ (см. рис. 4) ток, проходящий через гальванометр равным нулю и пренебрегая внутренними сопротивлениями источников ₂, определить ток I₁, проходящий через батарею ₁.

Задание по УИРС

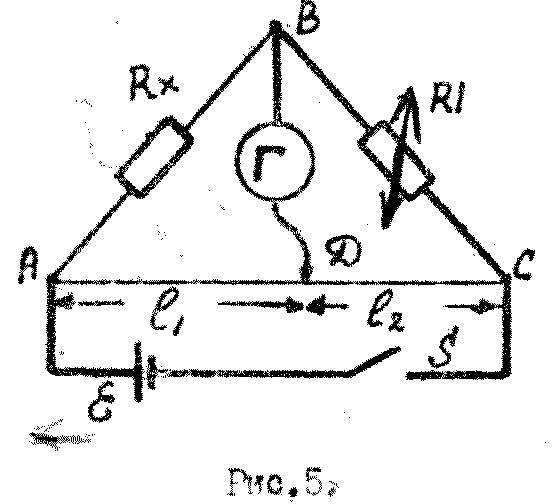
1. Докажите, что наименьшая погрешность измерения реохордным мостом (рис. 5) будет если l₁ = l₂. На рис. 5 АВ – проволока с высоким удельным сопротивлением, D – подвижный контакт.

2. Назовите пути увеличения точности моста Уитстона.

Работа №2

Исследование потенциального электрического поля

Приборы и принадлежности: электролитическая ванна с набором электродов, электронный вольтметр с зондом, выпрямитель ВС-24 выход переменного тока 0…..30 В.

Теоретическое введение

Исследование электростатического поля связано с рядом трудностей:

1. Зонд, вносимый в электростатическое поле, электризуется и искажает его;

2. Чувствительность имеющихся приборов не позволяет достаточно объективно изучить электростатическое поле.

Однако, изучение электростатического поля системы заряженных проводников можно заменить изучением поля электрического тока между той же системой проводников, если потенциалы проводников поддерживаются постоянными и проводимость среды во много раз меньше проводимости проводников. Такой способ изучения называют моделированием. В самом деле, оба поля потенциальны. Для них циркуляция напряженности E по любому замкнутому контуру l равна нулю

(1)

В слабо проводящей среде, как и в отсутствии тока (I = 0), поверхности проводников тоже можно считать эквипотенциальными.

. (2)

Выразив силу тока через плотность тока по замкнутой поверхности, получим . Но по закону Ома . Если среда однородная, то её удельная проводимость постоянная . Тогда поток напряженности электрического поля через замкнутую поверхность будет равен нулю

(3)

Пусть заряженные проводники помещены в безграничный диэлектрик. Для электростатического поля по теореме Остроградского-Гаусса

.

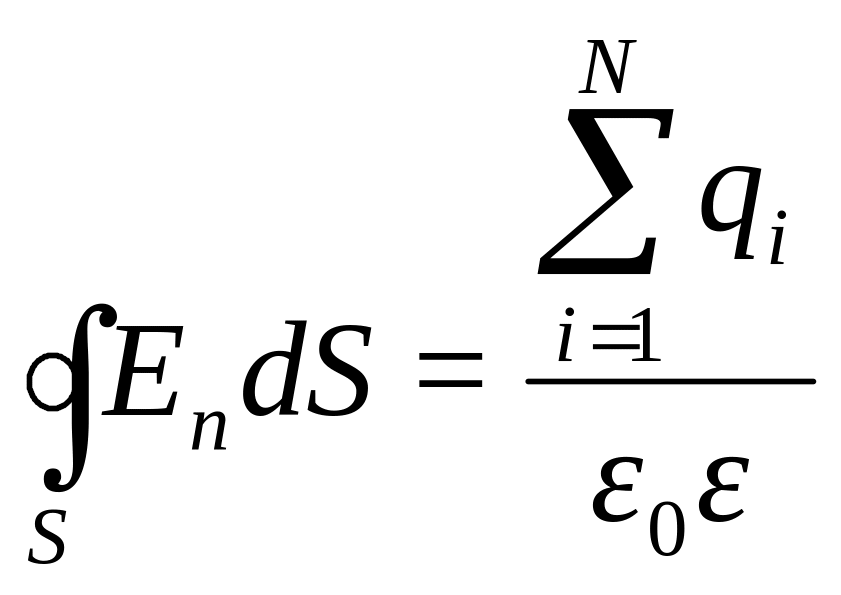Здесь E_n – проекция вектора напряженности на нормаль к элементу поверхности dS;

– интеграл по замкнутой поверхности S;

– сумма свободных зарядов внутри поверхности.

;

 – соответственно электрическая постоянная и диэлектрическая проницаемость среды. Для замкнутой поверхности, вне электродов, как для вакуума, так и для бесконечного поляризованного диэлектрика, .

Поэтому поток напряженности электростатического поля через замкнутую поверхность вне электродов будет равен нулю

(4)

Из уравнений (1), (2), (3), (4) следует, что электрическое поле в слабопроводящей, однородной среде совпадает с электростатическим полем, которое существовало бы между данными электродами, если бы между ними были то же напряжение, что и при наличии тока, а вместо проводящей среды был бы вакуум.