7.4 Проектирование участков механическим способом и его точность. Комбинирование способов при проектировании участков

Графический и аналитический спо­собы проектирования удобны в случае, когда линии и участ­ки имеют небольшое число пово­ротов и проектирование не требует больших затрат времени на произ­водство вычислений. При большой изломанности контуров землеполь­зовании применение планиметра де­лает процесс проектирования более простым, но менее точным.

Однако проектирование участков то­лько планиметром не выполняют, потому что планиметр - прибор, ко­торый по заданной площади и од­ному линейному измерению не дает возможности определить другое ли­нейное измерение. В связи с этим возника­ет необходимость проектировать участки последовательными прибли­жениями до тех пор, пока величина недостающей площади до задан­ной или излишек проектной площа­ди не будет превышать допусти­мой погрешности вычисления пло­щади.

Во избежание большого числа приближений при проектировании механический способ комбинируют с графическим, т. е. планиметром определяют площадь участка, спро­ектированного на глаз, а недостаю­щую или избыточную площадь про­ектируют графически треугольником или трапецией, в зависимости от условия проектирования.

В этом случае погрешность проектирования участка будет складываться из погрешности определения предварительно спроектированной площади планиметром погрешности проектирования недостающей или избыточной площади графическим способом. погрешности проектирования недостающей или избыточной площади вносят малую долю в общую погрешность проектируемой площади, поэтому погрешности проектирования участков планиметром можно считать равными погрешностям определения площадей планиметром и рассчитать по формулам (6.14), (6.15).

После вычисления площадей участков и получения допустимого расхождения, площади участков увязывают в сумме площадей конту­ров, сравнивают увязанные площади участков (полей) с заданными (расчетными), путем проектирования недостающих и избыточных площадей графическим способом приводят расположение границ в соответствие с заданными площадями участков (полей).

5. Исправление (спрямление) границ участков, способы решения задач в этих случаях

Необходимость спрямления границы возникает при уничтожении вклинивания в границы землепользований, при этом новую границу проводят с таким расчетом, чтобы площади землеполь­зований не изменились.

Новые границы проектируют в зависимости от требуемой точности графическим, механическим или аналитическим способом.

Рассмотрим несколько случаев спрямления границ.

В границе АВСDЕ (рис.7.3, а) нужно уничтожить вклинивание в землепользование М (точка С) и в землепользование N (точка D), при этом по эскизному решению новая граница должна проходить от точки В до линии DЕ.

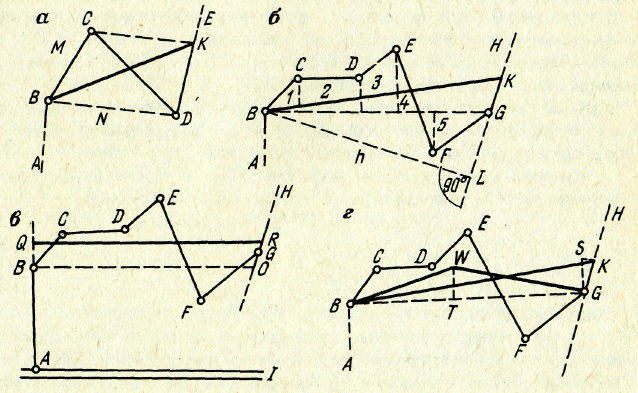
Рисунок 7.3 – Спрямление границ землепользований

Самое простое решение этой задачи графическим способом, без каких бы то ни было вычислений, состоит в том, что из точки С проводят на плане линию, параллельную BD, и в пересечении ее с линией DЕ получают проектную точку К. Линия ВК будет новой границей, потому что треугольники BСD и BКD равновелики, как имеющие общее основание и одинаковые высоты.

Другой вариант решения этой задачи состоит в графическом определении площади Р треугольника BСD, измерения по плану расстояния от точки В до линии DЕ, которое будет высотой h треугольника ВКD, после чего вычисляют

откладывают вычисленное расстояние от точки D, получают проект­ную точку К и проводят границу ВК.

При решении этой задачи аналитическим способом также можно применить несколько вариантов. Например, решением обратной геодезической задачи по координатам точек В и D вычисляют длину и дирекционный угол линии BD после чего вычисляют координаты точки К как пересечение двух линий, выходящих из точек С и D с ди-рекционными углами соответственно α_BD и α_DE.

Другой вариант решения этой задачи аналитическим способом заключается в вычислении площади Р треугольника BСD по координатам вершин или по углу С и сторонам BС и СD - формула (6.2), в вычислении длины и дирекционного угла линии ВD, после чего вычисляют

.

Аналогично спрямляют границы при большем числе поворотов. Пусть новая граница должна проходить от точки В (рис.7.3,6) до линии GН. При применении графического способа проводят линию через точки В и G, опускают на нее перпендикуляры из поворотных точек границы и вычисляют площадь Р фигуры ВСDЕFGB как алгебраическую сумму площадей фигур 1+2+3+4 -5. Затем определя­ют по плану расстояние от точки В до линии GН, которое будет высотой h треугольника ВGК, после чего вычисляют

.

Алгебраическую сумму площадей 1+2+3 + 4-5, т. е. площадь Р, можно определить планиметром. Если разность отсчетов получится от­рицательной, когда (1+2+3+4)<5, то это значит, что вычислен­ное основание GК надо откладывать от точки G не в направле­нии на точку H, а в обратном направлении по продолжению линии НG.

Вместо линии BG можно провести другую линию, которая не будет пересекать исправляемую границу, например, линию ВL, планиметром или графическим способом вычислить площадь фигуры ВСDЕFGL, определить по плану расстояние от точки В до линии GН, в данном случае величину ВL = h, после чего вычислить

.

Теперь, отложив от точки L расстояние LК, получают точку К и соединяют ее с точкой В.

При аналитическом способе проектирования алгебраическую сум­му Р = 1 + 2 + 3 +4 - 5 можно вычислить по координатам точек, записав их в ведомость в такой последовательности: В, С, D, Е, F, G, В. Решив обратную геодезическую задачу по координатам точек В и G, получают длину и дирекционный угол линии ВG, после чего вычисляют

.

Если новую границу требуется провести параллельно заданному направлению, например, параллельно дороге АI (рис.7.3, в), то следует предварительно провести линию ВО//А1, затем вычислить площадь Р фигуры ВСDЕFGОВ графическим способом или планимет­ром, после чего проектируют эту площадь трапецией, при этом новой границей будет линия АQRН.

При аналитическом способе проектирования сначала вычисля­ют координаты точки О как пересечение линий, выходящих из то­чек В и G, с дирекционными углами соответственно (А1) и (НG), затем по координатам точек В, С, D, Е, F, G, О вычисляют площадь Р₁, которую затем проектируют трапецией по основанию ВО и углам при этом основании (А1) — (АВ) и (GН) — (1А).

Спрямлять границы можно на местности, без плана. Например, для получения новой границы, выходящей из точки В (рис. 7.3, г), на линию ВG опускают перпендикуляры из точек С, D, Е, ..., измеряют длину линии ВG и длины перпендикуляров. По полученным измерениям вычисляют площади 1, 2, 3, 4, 5 (см. рис. 7.3,6), удвоенную алгебраическую сумму этих площадей делят на длину линии ВG, получают высоту

.

Эту высоту отмеряют на перпендикуляре, построенном при помощи экера из точки G, а из точки S строят другой перпендикуляр SK к линии GS до пересечения с линией GН в точке К. Линия ВК есть исправленная граница.