Основні закони алгебри логіки

закон переміщення

закон розподілення

сполучні закони

закон повторення

закон поглинання

закон доповнення

правило де Моргана

закон подвійного заперечення

закони склеювання

закони універсального множника

закон нульового множника

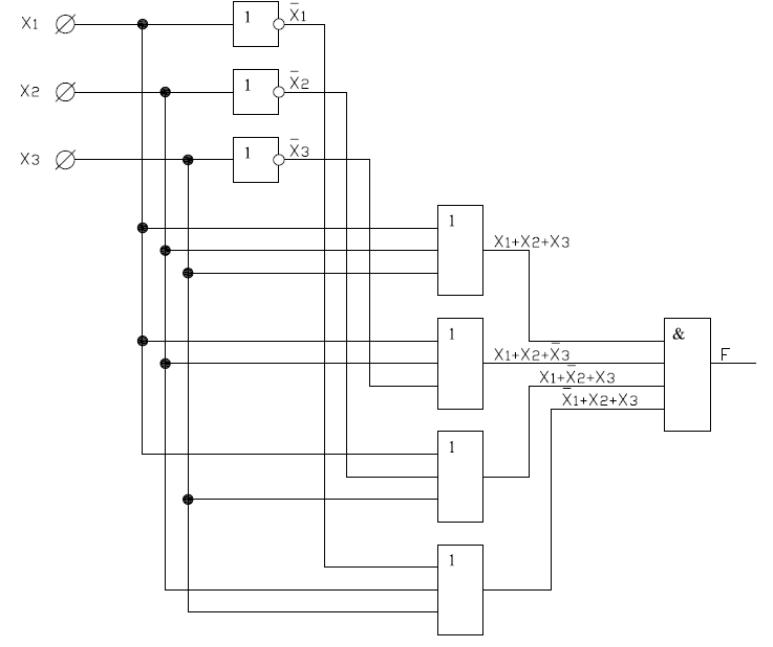
Рис. 1. Структурна схема для заданої логічної функції

Використання законів алгебри логіки спрощення логічних функцій

Спрощення функцій заданих в ДНФ або КНФ відбувається на основі закону склеювання з врахуванням законів повторення. Для прикладу спростимо функцію задану в КНФ.

Приклад 5. Мінімізація логічної функції заданої в КНФ. При мінімізації функції поданої в КНФ шукаємо дужки, які містять однакові аргументи і відрізняються лише одним. Враховуючи закон повторення одну дужку можемо використовувати декілька раз. Цей аргументи, що відрізняється пропаде. Для зручності пронумеруємо дужки. Тепер дужку 1 можна спростити з дужкою 2, дужку 3 з дужкою 1 та дужку 4 з дужкою 1.

В результаті отримаємо

перехід з одного виду подання функції в інший

При переході з одного виду подання в інший пригадуємо, що ДНФ записується для значень функції рівних 1, а КНФ для значень рівних 0. При переході з однієї форми подання функції до іншої необхідно інвертувати вираз функції та за правилом де Моргана загальну інверсію перенести на інверсію кожного аргументу з відповідною заміною знаків (І на АБО та АБО на І)

Приклад 6. Перетворення функції поданої в КНФ в ДНФ

Комбіновані логічні функції

Комбіновані логічні функції дозволяють створювати схеми логічних функцій використовуючи лише один тип елементів. Розглянемо дві комбіновані логічні функції АБО-НЕ та І-НЕ.

функція АБО‑НЕ

Функцію АБО‑НЕ можна знайти з функції АБО інвертувавши результат. Таблиця істинності для функції АБО‑НЕ буде мати вигляд

0	0	1
0	1	0
1	0	0
1	1	0

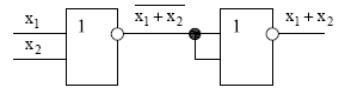
Використовуючи правило де Моргана подамо структурні схеми, що реалізують основні логічні функції (АБО, І, НЕ) на елементах 2АБО-НЕ

схема НЕ на елементах АБО-НЕ	схема АБО на елементах АБО-НЕ
схема І на елементах АБО-НЕ

Рис. 2. Структурні схеми основних логічних функцій на елементах 2АБО-НЕ

функція І‑НЕ

Функцію І‑НЕ можна знайти з функції І інвертувавши результат. Таблиця істинності для функції І‑НЕ буде мати вигляд

0	0	1
0	1	1
1	0	1
1	1	0

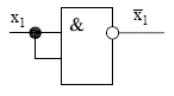
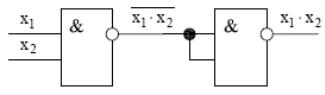
схема НЕ на елементах І-НЕ	схема І на елементах І-НЕ
схема АБО на елементах І-НЕ

Рис. 3. Структурні схеми основних логічних функцій на елементах 2І-НЕ

Приклад 7. Структурні схеми на елементах АБО-НЕ та І-НЕ для мінімізованої функції в КНФ. Для реалізації структурної схеми на елементах АБО-НЕ за правилом де Моргана зробимо перетворення для заміни логічного множення на логічне додавання.

Функція в КНФ

Перетворена функція для реалізації на елементах АБО-НЕ.

(1)

Для реалізації структурної схеми на елементах І-НЕ за правилом де Моргана зробимо перетворення для заміни логічного додавання на логічне множення. Перетворена функція буде мати вигляд:

(2)

На рис. 4 та рис. 5 відповідно подана структурна схема реалізація функції на елементах відповідно АБО-НЕ та І-НЕ.

Рис. 4. Структурна схема на елементах АБО-НЕ

Для реалізації цих схем ми використовували відповідно вирази (1) та (2) і приклади реалізацій основних логічних функцій подані на рис. 2 та рис 3.

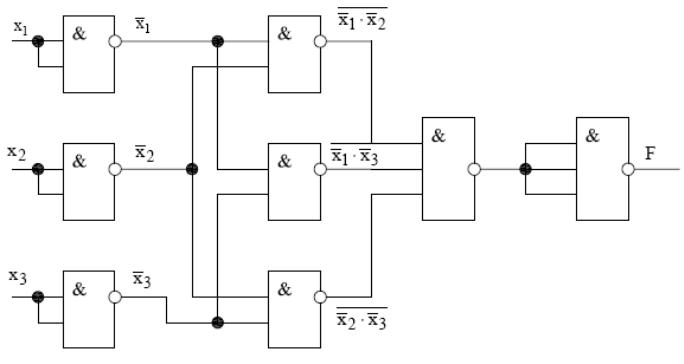
Рис. 5. Структурна схема на елементах І-НЕ

Приклад 8. Для заданої вище логічної функції та таблиці істинності, яка наведена в прикладі 2 можна побідувати принципову схему на дешифраторі КМІ55ИДІ2, яка показана на рис. 6. Так як для 4-ох комбінацій логічних змінних (011=3, 101=5, 110=6 та 111=7) значення функції дорівнює 1, то 4-відповідних виходи дешифратора під’єднюються до елемента АБО-НЕ та інвертора на елементі АБО-НЕ, так як після першого елемента АБО-НЕ ми отримуємо інвертоване значення заданої логічної функції.

Рис. 6. Складання принципової схеми для заданої логічної функції

на основі повного дешифратора КМІ55ИДІ2