
- •Тема 14. Статистические методы моделирования и прогнозирования социально-экономических явлений и процессов
- •14.1 Теоретико-методологические основы методов социально-экономического прогнозирования
- •14.2 Сущность методов социально-экономического прогнозирования. Классификация методов социально-экономического прогнозирования
- •14.3 Многомерный статистический анализ: сущность и виды
Тема 14. Статистические методы моделирования и прогнозирования социально-экономических явлений и процессов
14.1 Теоретико-методологические основы методов социально-экономического прогнозирования
В настоящее время ни одна сфера жизни общества не может обойтись без прогнозов как средства познания будущего. Важное значение при этом имеют прогнозы социально-экономического развития общества, обоснование основных направлений экономической политики, предвидение последствий принимаемых решений. Социально-экономическое прогнозирование является одним из решающих научных факторов формирования стратегии и тактики общественного развития.
Социально-экономическое предвидение основных направлений общественного развития предполагает использование специальных вычислительных и логических приемов, позволяющих определить параметры функционирования отдельных элементов в их взаимосвязи и взаимозависимости. Систематизированное научно обоснованное прогнозирование развития социально-экономических процессов осуществляется с первой половины 50-х годов 20 века, хотя некоторые методики прогнозирования были известны и ранее. К ним относятся логический анализ и аналогия, экстраполяция тенденций, опрос мнения специалистов и ученых.
Методология статистического прогнозирования предполагает построение и испытание многих моделей для каждого временного ряда, сравнение их на основе статистических критериев и отбор наилучших из них для прогнозирования.
В развитии методологии прогнозирования социально-экономических процессов большую роль сыграли научные разработки отечественных и зарубежных ученых А.Г. Аганбегяна, И.В. Бестужева-Лады, Л. Клейна, В. Гольдберга. В работах этих ученых рассматривается значение, сущность и функции прогнозирования, его роль и место в системе планирования, исследуются вопросы методологии и организации экономического прогнозирования, показываются особенности научного прогнозирования.
Развитие работ, освещающих вопросы прогнозирования, в настоящее осуществляется по таким основным направлениям, как:
- углубление теоретических и прикладных разработок нескольких групп методик, отвечающих требованиям разных объектов и разных видов работ по прогнозированию;
- разработка и реализация на практике специальных способов и процедур использования различных методических приемов в ходе конкретного прогнозного исследования;
- поиск путей и способов алгоритмизации методик прогнозирования и реализация их с использованием программных продуктов.
14.2 Сущность методов социально-экономического прогнозирования. Классификация методов социально-экономического прогнозирования
Под методами прогнозирования следует понимать совокупность приемов и способов мышления, позволяющих на основе анализа ретроспективных данных, экзогенных (внешних) и эндогенных (внутренних) связей объекта прогнозирования, а также их измерений в рамках рассматриваемого явления или процесса вывести суждения определенной достоверности относительно его (объекта) будущего развития.
По оценкам отечественных и зарубежных ученных, в настоящее время насчитывается свыше 20 методов прогнозирования, однако число базовых значительно меньше (15-20). Многие из этих методов относятся скорее к отдельным приемам и процедурам, учитывающим нюансы объекта прогнозирования. Другие представляют собой набор отдельных приемов, отличающихся от базовых или друг от друга количеством частных приемов и последовательностью их применения.
Наиболее широко применяются трендовые и адаптивные методы прогнозирования. Цель адаптивных методов – построение самонастраивающихся моделей, которые способны учитывать информационную ценность различных членов временного ряда и давать достаточно точные оценки будущих членов данного ряда. В основе адаптивного направления лежит простейшая модель экспоненциального сглаживания, основанная на вычислении экспоненциально взвешенной скользящей средней. Основные адаптивные методы прогнозирования: метод авторегрессии, скользящей средней (Бокса-Дженкинса и адаптивной фильтрации), экспоненциального сглаживания (модели Хольта, Брауна и экспоненциальной средней) и т. д.
Экстраполяцию, применяемую для поиска неизвестных членов ряда, в общем виде можно представить зависимостью (14.1):
![]() ,
(14.1)
,
(14.1)
где —
![]() прогнозируемый
уровень;
прогнозируемый
уровень;
yi — текущий уровень прогнозируемого ряда;
Т — период упреждения;
aj — параметр уравнения тренда.
В зависимости от того, какие принципы и исходные данные положены в основу прогноза, выделяются следующие простейшие методы экстраполяции:
среднего абсолютного прироста;
среднего темпа роста;
на основе выравнивания рядов по какой-либо аналитической формуле.
Прогнозирование по среднему абсолютному приросту применяется в том случае, когда есть основания считать абсолютную тенденцию линейной, т.е. метод основан на предположении о равномерном стабильном изменении уровня. В данном случае экстраполяция осуществляется по зависимости (14.2):
![]() ,
(14.2)
,
(14.2)
где —
![]() экстраполируемый
уровень;
экстраполируемый
уровень;
(i + t) — номер этого уровня (года);
i — номер последнего уровня (года) исследуемого периода, за который рассчитан ;
t — срок прогноза (период упреждения);
![]() —
средний абсолютный прирост.
—
средний абсолютный прирост.
Следует иметь в виду, что использование среднего абсолютного прироста для прогноза возможно только при выполнении следующего условия (14.3):
![]() ,
(14.3)
,
(14.3)
где
 ,
,
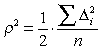 .
.
Прогнозирование по среднему темпу роста осуществляется в случае, когда установлено, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции необходимо определить средний коэффициент роста, возведенный в степень, соответствующую периоду экстраполяции (14.4):
![]() ,
(14.4)
,
(14.4)
где yi — последний уровень ряда динамики;
t — срок прогноза;
![]() —
средний коэффициент роста.
—
средний коэффициент роста.
При анализе рядов динамики иногда приходится прибегать к определению некоторых неизвестных уровней внутри данного ряда динамики, т.е. к интерполяции. Как экстраполяция, так и интерполяция могут проводиться на основе среднего абсолютного прироста, среднего темпа роста и с помощью аналитического выравнивания.
Важной управленческой задачей, решаемой с использованием рядов динамики, является определение общей тенденции развития. Одним из наиболее элементарных способов изучения общей тенденции в ряду динамики является укрупнение интервалов. Этот способ основан на укрупнении периодов, к которым относятся уровни ряда динамики.
Пример
Имеются данные о выпуске продукции группой предприятий по месяцам (млн. руб.):
Январь |
23,2 |
Июль |
28,4 |
Февраль |
19,1 |
Август |
24,1 |
Март |
22,3 |
Сентябрь |
26,3 |
Апрель |
25,1 |
Октябрь |
29,1 |
Май |
24,5 |
Ноябрь |
30,3 |
Июнь |
27,3 |
Декабрь |
26,5 |
Для выявления общей тенденции роста выпуска продукции произведем укрупнение интервалов. Для этой цели исходные (месячные) данные о выработке продукции объединяем в квартальные и получаем показатели выпуска продукции группой предприятий по кварталам:
I — 64,5;
II — 76,9;
III — 78,8;
IV — 85,9.
В результате укрупнения интервалов общая тенденция роста выпуска продукции данной группой предприятий выступает отчетливо:
64,5 < 76,9 < 78,8 < 85,9.
Выявление общей тенденции ряда динамики можно произвести также путем сглаживания ряда динамики с помощью метода скользящей средней. Сущность этого приема состоит в том, что по исходным уровням ряда (эмпирическим данным) определяют расчетные (теоретические) уровни. При этом посредством осреднения эмпирических данных индивидуальные колебания погашаются, и общая тенденция развития явления выражается в виде некоторой плавной линии (теоретические уровни).
Основное условие применения этого метода состоит в вычислении звеньев подвижной (скользящей) средней из такого числа уровней ряда, которое соответствует длительности наблюдаемых в ряду динамики циклов.
Недостатком способа сглаживания рядов динамики является то, что полученные средние не дают теоретических закономерностей (моделей) рядов, в основе которых лежала бы математически выраженная закономерность и это позволяло бы не только выполнить анализ, но и прогнозировать динамику ряда на будущее.
Значительно более совершенным приемом изучения общей тенденции в рядах динамики является аналитическое выравнивание. При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены усреднённо с помощью определенных математических функций. Путем теоретического анализа выявляется характер развития явления, и на этой основе выбирается то или иное математическое выражение типа изменения явления: по прямой, по параболе второго порядка, показательной (логарифмической) кривой и т.п.
Очевидно, что уровни временных рядов формируются под совокупным влиянием множества длительно и кратковременно действующих факторов, в т.ч. различного рода случайностей. Изменение условий развития явления приводит к более или менее интенсивной смене самих факторов, к изменению силы и результативности их воздействия и, в конечном счете, к вариации уровня изучаемого явления во времени.
