- •3. Пример решения задачи
- •3.1. Условие задачи.
- •3.2. Ограничения на значения параметров
- •3.3.Текст программы
- •3.4.Тестирование программы
- •Приложение. Некоторые стандартные математические функции.
- •Лабораторная работа № 2. Составление программ для решения геометрических и физических задач.
- •1. Цель работы
- •2. Темы для предварительной проработки
- •3. Пример решения задачи
- •3.1. Условие задачи.
- •3.2. Разработка алгоритма решения.
- •3.3. Ограничения на значения параметров
- •3.4.Текст программы
- •3.5. Результаты работы программы Результат работы программы может выглядеть, например, следующим образом:
- •Лабораторная работа № 3 Управление символьным выводом на экран
- •3. Пример решения задачи
- •Программы для решения задач с использованием условного оператора.
- •3.3. Текст программы
- •3.4. Результаты работы программы
- •Лабораторная работа № 5
- •1. Цель работы
- •2. Темы для предварительной проработки
- •3. Пример решения задачи
- •3.1. Условие задачи
- •3.2. Разработка алгоритма решения.
- •3.3. Определение переменных программы
- •3.4. Разработка текста программы
- •3.5. Отладка программы
- •3.2. Текст программы
- •Вычисление суммы ряда с помощью операторов цикла.
- •3.1. Условие задачи
- •3.2. Текст программы
- •3.3.Тестирование программы
- •Приближённое вычисление определённого интеграла методами прямоугольников, трапеций, Симпсона.
- •3.1. Задание
- •3.1.Текст программы
- •3.2.Тестирование программы
- •Использование вложенных циклов для решения ребусов.
- •3.1. Условие задачи
- •3.2.Используемые переменные
- •3.3. Разработка кода программы
- •3.4.Текст программы
- •3.5. Результат работы программы
- •3.1. Условие задачи
- •3.2. Используемые переменные
- •3.3.Текст программы
- •2.3.Тестирование программы
- •Задачи на формирование двумерных массивов.
- •3.3. Определение переменных программы
- •3.4. Разработка текста программы
- •Задачи на формирование двумерных массивов.
- •3.2. Текст программы
- •3.3. Тестирование программы
- •Рисование графических примитивов
Программы для решения задач с использованием условного оператора.
1. Цель работы
Целью лабораторной работы является получение практических навыков в работе с условным оператором и разветвленными алгоритмами в языке C++.
2. Темы для предварительной проработки
логические операции
условный оператор
3. Пример решения задачи
3.1. Условие задачи
Даны три положительных числа. Определить, можно ли построить треугольник со сторонами, длины которых равны этим числам. Если возможно, то ответить на вопрос, является ли он остроугольным.
3.2. Определение переменных программы и разработка алгоритма программы
Для того чтобы три числа a,b,c могли быть сторонами треугольника, нужно, чтобы сумма любых двух сторон была меньше третьей стороны.
Для того же, чтобы треугольник был остроугольным, необходимо, чтобы сумма квадратов любых двух сторон была больше квадрата третьей стороны.
3.3. Текст программы
//Лаб.раб.№ 2.Программирование ветвлений.
#include <iostream.h>
#include <conio.h>
void main()
{ float a,b,c;
clrscr();
cout<<"\nВведите 1 сторону треугольника: a=" ;
cin>>a;
cout<<"\nВведите 2 сторону треугольника: b=" ;
cin>>b;
cout<<"\nВведите 3 сторону треугольника: c=";
cin>>c;
if(a+b>c&&a+c>b&&b+c>a)
{ cout<<"\nТреугольник существует.";
if(a*a+b*b>c*c&&
a*a+c*c>b*b&&
c*c+b*b>a*a)
cout<<"\nОстроугольный.";
else cout<<"\nНе остроугольный.";
}
else cout<<"\nТреугольник не существует.";
getch();
}
3.4. Результаты работы программы
Ниже приведены результаты работы программы для различных входных данных:
Введите 1 сторону треугольника: a=3
Введите 2 сторону треугольника: b=4
Введите 3 сторону треугольника: c=5
Треугольник существует.
Не остроугольный.
Введите 1 сторону треугольника: a=3
Введите 2 сторону треугольника: b=5
Введите 3 сторону треугольника: c=5
Треугольник существует.
Остроугольный.
Введите 1 сторону треугольника: a=2
Введите 2 сторону треугольника: b=2
Введите 3 сторону треугольника: c=5
Треугольник не существует.
Лабораторная работа № 5
Условный оператор в языке С++
(Области, описываемые логическими выражениями)
1. Цель работы
Целью лабораторной работы является получение практических навыков в работе с условным оператором и разветвленными алгоритмами в языке C.
2. Темы для предварительной проработки
логические операции
условный оператор
3. Пример решения задачи
3.1. Условие задачи
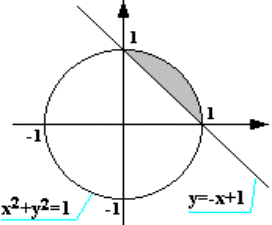
Написать программу, которая вводит координаты точки (x, y) и определяет, попадает ли точка в заштрихованную область на рисунке. Попадание на границу области считать попаданием в область.
3.2. Разработка алгоритма решения.
Первым шагом алгоритма должен быть ввод координат точки: x и y. Для большего удобства при анализе результатов можно вывести введенные значения на экран. Исследование изображения на рисунке-задании дает нам основание утверждать, что целевая область образуется пересечением: прямой с коэффициентом -1 и смещением +1 и окружности с центром в начале координат и радиусом 1, как показано на рисунке справа |
|
Уравнение этой прямой: y=-x+1
Уравнение окружности:
![]()
Для проверки попадания
точки в заданную область нужно проверить
условия того, что:
1).
Точка лежит выше прямой или на ней, т.е.:
y>=-x+1
2).
Точка лежит внутри окружности или на
ней, т.е.:
![]() Точка
лежит в области, если выполняются оба
условия, если же не выполняется хотя бы
одно из них, точка лежит вне области.
Следовательно, эти условия должны быть
объединены логической операцией "И".
Точка
лежит в области, если выполняются оба
условия, если же не выполняется хотя бы
одно из них, точка лежит вне области.
Следовательно, эти условия должны быть
объединены логической операцией "И".