§21.Момент инерции.

Определение: Моментом инерции материальной точки относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой точки при вращательном движении и, равная произведению её массы на квадрат расстояния до оси, т.е. , а также, где- угловая скорость тела относительно данной оси.

Определение: Моментом инерции системы материальных точек относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой системы при вращательном движении и, равная алгебраической сумме произведений масс всех материальных точек системы на квадрат их расстояний до оси, т.е. .

Момент инерции определен только относительно оси.

В случае непрерывного распределения масс с плотностью сумма за­менится на интеграл по всему объему тела: (Интегрирование производится по всему объёму; пределы интегрирования устанавливаются исходя из конфигурации тела и его размеров). Если тело однородно, то его плотность во всех точках постоянна и можно вынести из-под знака интеграла.

Найдем моменты инерции для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему, т.е. .

1. Момент инерции обручаотносительно оси, перпендикулярной к его плоскости и проходящей через его центр.

Обруч считается бесконечно тонким, т.е. толщиной обода можно пре­небречь по сравнению с радиусом R.. Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, R²можно вынести из-под знака интеграла:, гдеm— полная масса обруча.

2. Момент инерции дискаотносительно оси, перпендикулярной его плоскости и проходящей через центр. Диск считается бесконечно тонким, т.е. его толщина много меньше ра­диуса R.Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие обручи радиусомsи толщинойds (См.рис.).

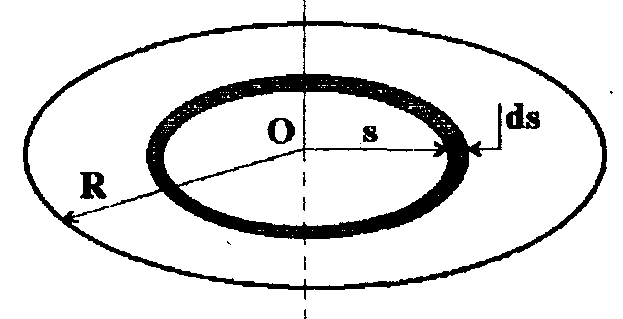
Момент инерции диска относительно перпендикулярной оси, проходящей через центр.

Площадь поверхности обруча равна произведению его длины на толщину: 2  s ds.Поскольку массатдиска распределена равномерна, масса обручаdmпропорциональна площади его поверхности:

.

Момент инерции обруча мы уже знаем: . Осталось просуммировать моменты инерции всех таких обручей:.

Такой же результат получится и для момента инерции цилиндра конеч­ной длины относительно его продольной оси.

3. Момент инерции шараотносительно его диаметра. Поступим аналогичным образом: "нарежем" шар на бесконечно тон­кие диски толщинойdz.находящиеся на расстоянииzот центра (См.рис.).

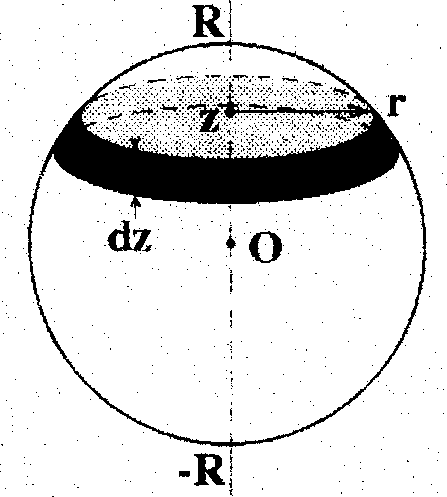
Момент инерции шара относительно диаметра.

Радиус такого диска равен . Объем дискаdV_z равен произведению его площади на толщину:

. Массу дискаdmнаходим, разде­лив массу шаратна его объем, умножив на объем диска:

.

Момент инерции диска был найден выше. В применении к данному слу­чаю, он равен:

.

Момент инерции шара находится интегрированием по всем таким дискам:

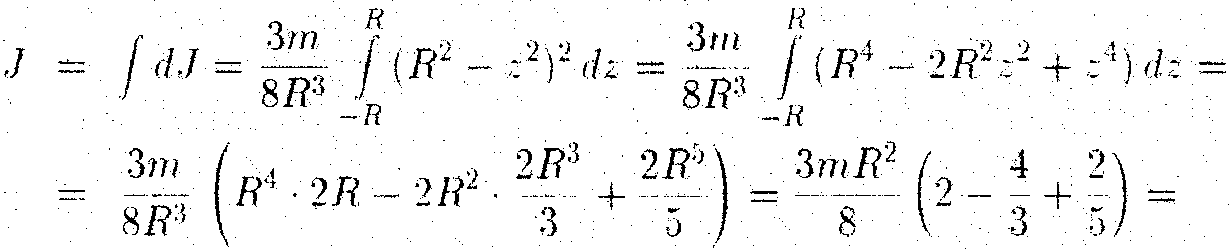
4.Момент инерции тонкого стержняотносительно оси, проходящей через его середину перпендикулярно стержню.

Пусть стержень имеет длину ℓ.Направим осьxвдоль стержня. Начало координат по условию находится в центре стрежня. Возьмем эле­мент стержня длинойdx.находящийся на расстоянииxот оси враще­ния. Его масса равна

dm = (m/ℓ) dx,а момент инерцииdJ=(m/ℓ) x²  dx. Отсюда находим момент инерции стрежня:

(*).

Момент инерции величина аддитивная, т.е. суммарный момент инерции системы тел относительно какой-либо оси, равен сумме моментов инерции каждого из тел данной системы относительно той же оси:

Физический смысл момента инерции:Инерционные свойства при поступательном движении характеризуются только массой тела, т.е. зависит только от массы. Инерционные свойства при вращательном движении характеризуются моментом инерции, т.е. зависят от его массы, расстояния до оси вращения и расположению теда по отношению к этой оси. Последнее означает, что относительно двух разных осей инерционные свойства вращательного движения одного и того же движения тела будут разными. Пример.