Лабораторная работа 31

МОСТ ПООСТОЯННОГО ТОКА

Задачи работы

1. Определение сопротивления проводников с помощью моста постоянного тока.

2. Расчет удельного сопротивления проводников.

Физическое обоснование эксперимента

Электрический ток в металлах – проводниках 1-го рода – обусловлен направленным (упорядоченным) движением электронов под действием приложенного электрического поля. Такие электроны называются “свободными” из-за сравнительно слабой связи с ионами кристаллической решетки, внутри которой они могут свободно перемещаться.

Сила тока I, текущего по однородному металлическому проводнику при отсутствии на нем сторонних сил, согласно закону Ома, пропорциональна напряжению U на проводнике (разности потенциалов электрического поля), приложенному к концам проводника:

, (31.1)

где:R– электрическое сопротивление проводника.

Величина сопротивления зависит от геометрической формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника диаметром d сопротивление проводника определяется по формуле:

, (31.2)

где 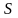– площадь его поперечного сечения, а r – коэффициент, зависящий от свойств материала, называемый удельным электрическим сопротивлением,L– длина проводника. При L= 1 м и S= 1 м², R=r, т.е. коэффициент r, численно равен сопротивлению проводника единичной длины и единичного поперечного сечения. В системе СИ r, измеряется в Ом-метрах (Ом м).

Какова физическая природа электрического сопротивленияR?

Согласно классической теории электроны проводимости в металлах ведут себя как частицы идеального газа. Двигаясь упорядоченно, они взаимодействуют (упруго сталкиваются) с положительными ионами в узлах кристаллической решетки, и изменяют направленность своего движения (рассеиваются).

Однако классическая теория натолкнулась на трудности в вопросе о теплоемкости электронного газа. Кроме того, экспериментально наблюдаемая пропорциональность удельного сопротивления r температуре также не могла быть объяснена с классической точки зрения.

Эти проблемы были преодолены в квантовой механике, которая рассматривает движение электрона как распространение волны. Электронные волны рассеиваются на неоднородностях, всегда существующих в кристаллической решетке. В случае идеальной решетки неоднородности, рассеивающие волны, связаны лишь с тепловым движением (колебаниями) решетки, что ведет к пропорциональности удельного сопротивления 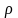температуре кристалла t. При наличии примесей в кристаллической решетке имеются неоднородности, не зависящие от температуры, поэтому связь удельного сопротивления r с температурой принимает вид:

,

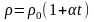где r₀,– значение удельного сопротивления металла при температуре 0⁰С, t– температура, a– температурный коэффициент сопротивления.

Для большинства металлов при температурах, близких к комнатной, r изменяется пропорционально абсолютной температуре T. При низких температурах наблюдается отступление от этой закономерности. В большинстве случаев, при 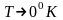, , 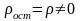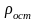– это, так называемое, остаточное сопротивление, которое зависит от свойств и чистоты материала, наличия остаточных механических напряжений в металле.

Если известно сопротивление однородного цилиндрического проводника R, то расчет удельного сопротивления r производится по формуле:

, (31.3)

Существуют несколько способов измерения R:

а) прямое измерение омметром;

б) косвенное измерение с помощью вольтметра и амперметра;

с) измерение с помощью моста постоянного тока, называемого также мостом Уитстона. Мостовой метод является наиболее точным, так как позволяет исключить погрешности, вносимые омметром, вольтметром и амперметром. Подробнее о погрешностях электроизмерительных приборов можно прочитать в Части V описания лабораторных работ “Электричество. Переменный ток ”.

Измерение сопротивления проводников с помощью моста постоянного тока

Рассмотрим принципиальную схему четырехплечевого моста постоянного тока. Четыре сопротивления (четыре плеча) R₁, R₂, R₃, R₄, соединены в четырехугольник ADBC (рис.31.1). Сопротивление R₄ = Rx является измеряемым, остальные три известны, причем, по крайней мере, одно из них (в данном случае R₃) является регулируемым. В одну из 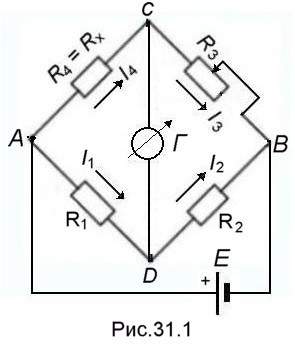диагоналей моста AB включен источник питания, во вторую – магнитоэлектрический нулевой индикатор – обычно гальванометр Г. Гальванометр является высокочувствительным прибором, предназначенным для измерений очень малых токов (менее 10^-6 А).

Меняя величину регулируемого сопротивления, можно добиться такого состояние схемы, при котором напряжение (разность потенциалов) между точками С и D, и, следовательно, ток в гальванометре Г равны нулю. Это состояние называют состоянием равновесия моста (мост сбалансирован).

Состояние равновесия наступает только при определенном соотношении плеч моста – сопротивлений .

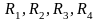Обозначим 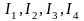– силу токов, текущих по соответствующим плечам, ток через гальванометр – , а потенциалы в точках А, В, С, D – V_A, V_B, V_C, V_D. Если мост сбалансирован (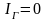 ), то

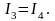V_С = V_D. (31.4)

По закону Ома имеем:

I₁ = (V_A – V_D)/R₁, I₂= (V_D– V_B)/R₂,

I₄ = (V_A – V_C)/R₄ I₃ = (V_C – V_В)/R₃,

Деля I₄ на I₁, а I₃ на I₂ и принимая во внимание равенства (31.4), получим,

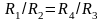(31.5)

Таким образом, если ток в гальванометре отсутствует, то неизвестное сопротивление можно выразить через три другие сопротивления

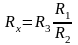, (31.6)

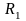где – плечо сравнения, и 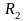– плечи отношения. Из (31.6) видно, что измерение сопротивления 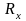сводится к регулировке плеча сравнения при постоянном отношении 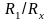, (либо к регулированию отношения 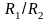при постоянном значении ) до исчезновения тока в гальванометре. При этом является сопротивлением всего плеча моста, ограниченного узлам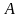и и , включая сопротивления соединительных проводов и сопротивления всех контактов между этими точками. Если измеряемое сопротивление много больше сопротивления проводов и контактов (которые трудно сделать меньше нескольких тысячных долей ома), то измерение может быть произведено с достаточно высокой точностью. Однако, если мало (меньше 1 Ом), то погрешность определения велика, и надо применять более сложные мостовые схемы. При измерении больших сопротивлений (больше 100 кОм) погрешности возможны из-за токов утечки, которые могут появляться вследствие соизмеримости сопротивлений изоляции моста и измеряемого сопротивления. Поэтому большие сопротивления измеряют с помощью других методов. Четырехплечевой мост постоянного тока обычно применяется для измерения сопротивлений в пределах от 1 Ом до 100 кОм.

Метод измерений сопротивлений с помощью моста – это метод сравнения или нулевой метод: неизвестное сопротивление сравнивается с известным, а гальванометр служит индикатором отсутствия тока в диагонали моста. Следовательно, точность измерения обусловлена точностью изготовления известных сопротивлений и чувствительностью гальванометра (чувствительностью моста).

Можно показать, что чувствительность моста максимальна, когд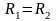а , т.к. при этом погрешность измерения – минимальна.