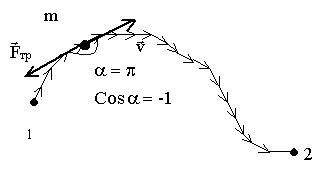5.6.1. Консервативность силы тяжести

На приведенном выше рисунке дан вид сбоку. Точка m движется под действием силы тяжести из 1 в 2. Сила тяжести всегда направлена вниз! вектор перемещения,

.

При любой траектории ответ будет таким же, значит, сила тяжести консервативна.

5.6.2. Неконсервативность силы трения

На рисунке изображен вид сверху на материальную точку m, движущуюся при наличии силы трения из положения 1 в положение 2. Сила трения всегда направлена против скорости cosα = -1.

.

Ответ зависит от выбора траектории, значит, сила трения неконсервативна.

5.7. Потенциальная энергия может быть введена только для поля консервативных сил

Так как их работа не зависит от траектории, а только от начального и конечного положений материальной точки, то эту работу можно записать в виде разности двух чисел: одно - W_n1 - будет зависеть от начального положения тела, второе - W_n2 - от конечного положения тела.

.

W_n1 - потенциальная энергия тела в положении 1; W_n2 - в положении 2.

5.7.1. Некоторые конкретные выражения для потенциальной энергии W_n(r) Для нахождения конкретного вида зависимости W_n(r) необходимо вычислить работу

.

В частности, для однородного поля тяжести, где , используя(5.6.1), получим: W_n = mgh. Если - гравитационная сила, тоЕсли- кулоновская сила, то. Если- сила упругости, то.

5.8.Закон сохранения механической энергии

5.8.1.Для одной материальной точки, движущейся в поле консервативных сил, из (5.5)

A₁₂ = W_k2 - W_k1,

из (5.7)

A₁₂ = W_n1 - W_n2.

Откуда

W_n1 - W_n2 = W_k2 - W_k1

или

W_k1 + Wn1 = W_k2 + W_n2.

В поле консервативных сил сумма кинетической и потенциальной энергии материальной точки остается постоянной, т.е. сохраняется.

- полная энергия материальной точки.

Полная энергия материальной точки в поле консервативных сил сохраняется.

5.8.2. Полная энергия системы материальных точек Для системы, состоящей из N взаимодействующих между собой материальных точек, полная энергия

,

где W_{п i, k} - потенциальная энергия взаимодействия i -й материальной точки с k-й материальной точкой. W_п - потенциальная энергия взаимодействия всех частиц системы между собой.

5.8.2.1. Закон сохранения энергии для системы материальных точек Если система материальных точек находится во внешнем поле консервативных сил, то еЈ полная механическая энергия

,

где W'_п - потенциальная энергия системы во внешнем поле. Полная механическая энергия системы материальных точек, находящейся только под действием консервативных сил, остается постоянной. При наличии неконсервативных сил полная механическая энергия системы не сохраняется, ее убыль равна работе неконсервативных сил.

6. Кинематика вращательного движения

6.1. Поступательное и вращательное движение

В данном примере траектория центра масс - окружность, остальные точки тела также движутся по окружностям , но центры этих окружностей не лежат на одной прямой.

а) поступательное движение. Любая линия, проведенная в твердом теле, при движении остается параллельной самой себе.

Здесь, как и в предыдущем примере а), центр масс тела движется по той же окружности.

б) вращательное движение, центр масс движется по окружности того же радиуса. Каждая точка твердого тела движется по своей окружности; центры всех окружностей лежат на прямой, называемой осью вращения.