- •Учебное пособие для студентов технических университетов
- •1. Вводные сведения
- •1.1. Предсказание будущего - задача науки
- •1.2. Предмет физики
- •1.3. Физическая модель
- •1.4. Язык физики?
- •1.5. Экспериментальная и теоретическая физика
- •Физические основы механики
- •3.1.3. Абсолютно твердое тело
- •3.2. Тело отсчета
- •3.3. Система отсчета
- •3.4. Положение материальной точки в пространстве
- •3.10.1. Нормальное и тангенциальное ускорение
- •4. Динамика материальной точки
- •4.6.1. Система си (System international)
- •4.6.1.1. Размерность силы
- •5.3. Работа
- •5.6.1. Консервативность силы тяжести
- •5.6.2. Неконсервативность силы трения
- •5.7. Потенциальная энергия может быть введена только для поля консервативных сил
- •5.8.Закон сохранения механической энергии
- •6. Кинематика вращательного движения
- •6.1. Поступательное и вращательное движение
- •6.2. Псевдовектор бесконечно малого поворота
- •6.5. Связь линейной скорости материальной точки твердого тела и угловой скорости
- •8. Элементы специальной теории относительности
- •8.2. Принцип относительности Галилея:
- •8.3. Неудовлетворительность механики Ньютона при больших скоростях
- •8.5.1. Вывод преобразований Лоренца
- •8.6. Следствия из преобразований Лоренца
- •9.3. Электрическое поле
- •9.3.6. Принцип суперпозиции электрических полей
- •9.3.7. Напряженность поля точечного заряда
- •9.3.8. Линии напряженности
- •9.3.9. Линии напряженности точечных зарядов
- •9.4.4.1. Поле равномерно заряженной бесконечной плоскости
- •9.4.4.3. Поле однородно заряженного бесконечного цилиндра
- •9.9. Проводник в электрическом поле
- •9.10. Электроемкость уединенного проводника
- •9.11. Электроемкость конденсатора
- •9.12. Энергия электрического поля
- •9.12.1. Плотность энергии электрического поля в вакууме
- •9.13. Электрическое поле в диэлектрике
- •9.13.1. Диэлектрик?
- •9.13.1.1. Два типа диэлектриков - полярные и неполярные
- •9.13.2. Поляризованность диэлектрика (вектор поляризации) - это дипольный момент единицы объема:
- •9.13.4.1. Плотность энергии электрического поля в диэлектрике
- •10.4. Закон Ома для участка цепи
- •10.5. Закон Ома в дифференциальной форме
- •10.6. Закон Джоуля-Ленца в дифференциальной форме
- •Магнетизм. Уравнения Максвелла
- •11.5.6. Магнитное поле тороида
- •11.6. Закон Ампера
- •11.7. Сила Лоренца - это сила, действующая со стороны магнитного поля на движущийся в нем заряд
- •11.7.1. Движение заряженной частицы в однородном магнитном поле
- •11.8. Рамка с током в магнитном поле
- •11.11.1. Потокосцепление
- •11.11.2. Индуктивность соленоида
- •11.11.3. Энергия магнитного поля
- •12. Магнитное поле в веществе
- •12.2. Классификация магнетиков
- •13. Уравнения Максвелла
- •13.3. Система уравнений Максвелла в интегральной форме
- •13.4. Система уравнений Максвелла в дифференциальной форме
9.3. Электрическое поле
9.3.1. Заряд - источник поля. Всякий покоящийся заряд создает в пространстве вокруг себя только электрическое поле. Движущийся - еще и магнитное.
9.3.2. Заряд - индикатор поля. О наличии электрического поля судят по силе, действующей на неподвижный положительный точечный заряд, помещенный в это поле (пробный заряд).
9.3.3. Напряженность - силовая характеристика электрического поля. Если на неподвижный точечный заряд qпр. действует сила, то значит, в точке нахождения этого заряда существует электрическое поле, напряженность которого определяется так:
|
|
|
|
9.3.4. Единица напряженности в системе СИ имеет название вольт на метр (В/м), при такой напряженности на заряд в 1 Кл действует сила в 1 Н. Происхождение размерности В/м см (9.7) .
9.3.5.
Знаем напряженность - найдем силу
Если
в каждой точке пространства нам известна
напряженность электрического поля
![]() ,
то мы можем найти силу, действующую на
точечный заряд, помещенный в точку r(9.3.3)
,
то мы можем найти силу, действующую на
точечный заряд, помещенный в точку r(9.3.3)
![]() .
.
9.3.6. Принцип суперпозиции электрических полей
|
|
Из (9.2.4) следует, что поля складываются, не возмущая друг друга. Если поле создано системой зарядов, то результирующее поле равно векторной сумме полей отдельных зарядов:
|
9.3.7. Напряженность поля точечного заряда
|
|
Задача
- найти напряженность поля, созданного
в точке
|
Решение:
а)
поместим в точку
![]() пробный
заряд qпр
и
найдем по закону Кулона (9.2.2)
силу,
действующую на пробный заряд:
пробный
заряд qпр
и
найдем по закону Кулона (9.2.2)
силу,
действующую на пробный заряд:
![]() ;
;
б) воспользуемся определением напряженности электрического поля (9.3.3):
![]() .
.
Для модуля напряженности:
 .
.
Ответ:
напряженность поля, созданного в точке
![]() точечным
зарядом q, прямо пропорциональна величине
этого заряда (создающего поле, заряда
- источника поля) и обратно пропорциональна
квадрату расстояния от заряда - источника
поля до точки, где ищется поле.
точечным
зарядом q, прямо пропорциональна величине
этого заряда (создающего поле, заряда
- источника поля) и обратно пропорциональна
квадрату расстояния от заряда - источника
поля до точки, где ищется поле.
!!! Пробный заряд в ответ не входит!
 .
.
9.3.8. Линии напряженности
Для графического изображения электрического поля используются линии напряженности (силовые линии). Их строят по следующим правилам:
|
9.3.8.1. Линии напряженности |
начинаются на положительных зарядах, заканчиваются на отрицательных или уходят в бесконечность. |
|
|
|
9.3.8.2. Вектор напряженности |
направлен по касательной к линии напряженности в каждой точке. |
|
|
|
9.3.8.3. Густота линий |
пропорциональна модулю напряженности электрического поля. |
|
|
9.3.9. Линии напряженности точечных зарядов
|
|
|
|
|
|
|
|
9.4. Теорема Гаусса
9.4.1. Поток вектора напряжeнности электрического поля
9.4.1.1. - Поток
вектора
![]() для
однородного поля
для
однородного поля
Для
![]()
![]()

Здесь
![]() -
вектор нормали к поверхности S.
-
вектор нормали к поверхности S.
9.4.1.2. Поток вектора
![]() через
бесконечно малую площадку в неоднородном
поле
через
бесконечно малую площадку в неоднородном
поле
|
|
Как и в (9.4.1.1):
|
9.4.1.3. Поток вектора
![]() через
произвольную поверхность в неоднородном
поле
через
произвольную поверхность в неоднородном
поле

9.4.1.4. Поток пропорционален числу силовых линий Ф пропорционален числу линий напряженности, проходящих через площадь S (9.3.3) и (9.3.8)
9.4.2. Поток вектора
![]() через
сферу (для
поля точечного заряда).
через
сферу (для
поля точечного заряда).
9.4.2.1. Заряд - в центре сферы На поверхности сферы поле постоянно по величине (9.3.7.):
 .
.
В любой точке сферы поле направлено перпендикулярно ее поверхности, т.е.
 .
.
|
|
Из (9.4.1.3):
|
Мы получили, что:
 .
.
9.4.2.2. Заряд в произвольном месте внутри сферы
 .
.
Поток Ф пропорционален числу силовых линий, проходящих через сферу, а их число не изменяется при изменении положения заряда внутри сферы, т.е. поток тоже будет постоянным:
 .
.
9.4.2.3. Поток вектора
![]() поля
точечного заряда через "измятую"
сферу - произвольную поверхность
Число
проходящих через "измятую" сферу
силовых линий не изменилось, т.е.
поля
точечного заряда через "измятую"
сферу - произвольную поверхность
Число
проходящих через "измятую" сферу
силовых линий не изменилось, т.е.
 .
.
Эта формула верна для потока вектора Е поля точечного заряда, расположенного ВНУТРИ замкнутой поверхности произвольной формы.
"Измятая" сфера:

9.4.2.4. Поток вектора Е поля системы зарядов, находящихся внутри замкнутой поверхности
|
|
Т.к.
Для
произвольного числа зарядов N:
|
9.4.2.5. Поток вектора Е для поля, созданного зарядами, находящимися вне замкнутой поверхности
|
|
Силовая линия дважды проходит через замкнутую поверхность, один раз она учитывается со знаком "+", другой раз - со знаком "-". В результате поток в этом случае Ф = 0. |
9.4.3. Формулировка теоремы Гаусса
|
|
Из (9.4.2.4) и (9.4.2.5) следует, что поток вектора напряженности электрического поля через ЛЮБУЮ замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности, деленной на ε0:
|
Из (9.4.1.3)
![]() ,
тогда теорема Гаусса запишется так:
,
тогда теорема Гаусса запишется так:

9.4.4. Применение теоремы Гаусса для вычисления полей. Теорема Гаусса:

S - любая замкнутая
поверхность,
![]() -
сумма зарядов внутри S.
Применяя
теорему Гаусса, мы должны:
-
сумма зарядов внутри S.
Применяя
теорему Гаусса, мы должны:
а) САМИ выбрать
конкретную гауссову поверхность S,
такую, чтобы интеграл по этой поверхности
легко считался. Затем найти
![]() ;
;
б) посчитать сумму зарядов внутри выбранной нами S;
в) приравнять результат полученный в пункте а), к результату, полученному в пункте б), деленному на ε0.


 .
.
 .
.
 а)
поле положительного заряда
а)
поле положительного заряда  б)
поле отрицательного заряда
б)
поле отрицательного заряда в)
поле двух разноименных зарядов
в)
поле двух разноименных зарядов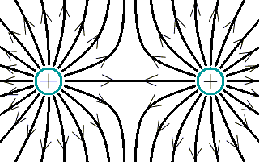 г)
поле двух одноименных зарядов
г)
поле двух одноименных зарядов