1.3. Эластичность линейной кривой спроса

Рассмотрим линейную кривую спроса Q=a-bP. Наклон этой кривой спроса есть константа(-b). –b= .Подставив значение –b в формулу (3), получим . Для линейной кривой спроса наклон – постоянная величина, он не зависит от цены и величины спроса. Напротив, с изменением цены отношение P/Q меняется при движении вдоль кривой спроса (рис. 7).

Следовательно, для линейной кривой спроса эластичность спроса по цене – переменная величина.

При Р=0 эластичность спроса равна нулю. При Q=0 коэффициент эластичности спроса равен минус бесконечности. Если Q=a/2, P=a/2b, то эластичность спроса по цене E= -1. Таким образом, точка единичной эластичности спроса по цене находится в середине линии спроса.

Спрос является

• неэластичным при ;

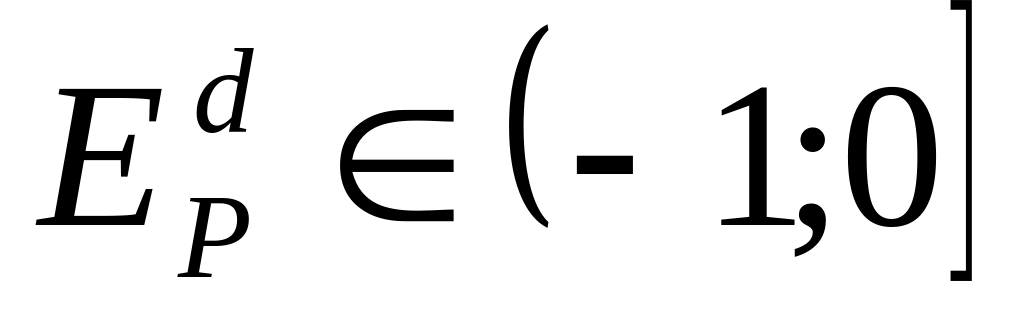• эластичным при .

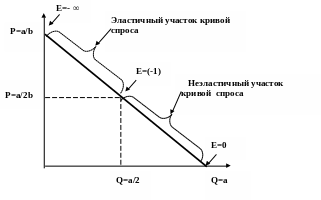
Рис. 7

Пример 3.

Дана функция спроса на товар Qd = 9 – 0,5Р. Определить коэффициент эластичности спроса по цене составит при цене 6 ден. ед.

Решение:

По формуле точечной эластичности , откуда .

Ответ: -0,5.

Пример 4.

Функция спроса имеет следующий вид: Qd = 2100 – 3P. При какой цене ценовая эластичность спроса (Е_Р) составит (-0,75)?

Решение: , откуда . Получаем, что Р=300.

Ответ: 300.

1.4 Функция спроса с постоянной эластичностью

Рассмотрим эластичность функции спроса: вида: (Рис.8)

где А и а - некоторые константы. Выведем формулу эластичности для этой функции:

Таким образом, мы выяснили, что значение эластичности для подобной гиперболической функции спроса не зависит от координаты точки и при любом уровне цены равно -а. Обратите внимание, что свойством постоянной эластичности обладает не всякая гиперболическая функция спроса, а только удовлетворяющая указанному выше общему уравнению.

Рис. 8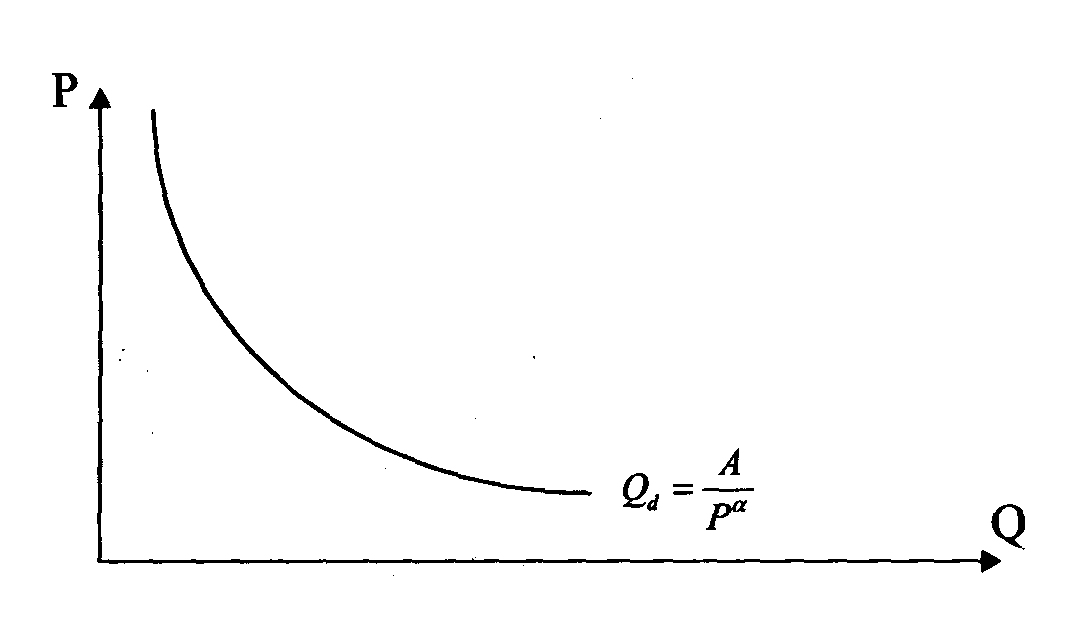

1.5. Эластичность и общий доход

Общий доход (выручка) определяется как произведение цены на проданное количество товара. ТR=P∙Q.Выясним, как общая выручка зависит от эластичности спроса при линейной функции спроса: Q=a-bP. Выручка - прямая функция от объема продаж: TR= F(Q). Чтобы ее определить, надо выразить цену товара через Q: Р= (обратная функция спроса) и подставить это выражение в ТR: ТR=P∙Q=( )∙Q. Графическое представление функции – это парабола, ветви которой опущены вниз. Вершина параболы (максимум выручки) достигается при Q=a/2; P=a/2b, то есть при единичной эластичности спроса. При снижении цены товара (синяя стрелка на графике) общая выручка продавцов возрастает от нуля до максимума на эластичном участке кривой спроса, а затем она снижается от максимального значения до нуля на неэластичном участке кривой спроса.

При снижении цены товара (красная стрелка на графике) общая выручка продавцов возрастает от нуля до максимума на неэластичном участке кривой спроса, а затем она снижается от максимального значения до нуля на эластичном участке кривой спроса.

Если спрос на товар эластичен по цене, то цена и общая выручки изменяются в противоположных направлениях: P↓- TR↑; P↑- TR↓.

Если спрос на товар неэластичен по цене, то цена и общая выручка изменяются в одном направлении:

P↓- TR↓; P↑- TR↑.

Рассчитаем выручку для нелинейной функции спроса вида .

TR= . Таким образом, выручка постоянна и не зависит от Р и Q

Рис.9

Пример 5.

По исходным данным, приведенным в таблице, определите общую выручку, коэффициент эластичности спроса по цене, тип эластичности спроса по цене для товаров A, B, С.

Таблица 1
	Товар А		Товар В		Товар С
Показатель	В начале периода	В конце периода	В начале периода	В конце периода	В начале периода	В конце периода
Цена, тыс. р.	4	3	10000	5000	500	250
Количество шт.	100	120	10	30	20	40
Выручка, тыс. р.
Коэффициент эластичности
Тип эластичности

Решение: Общую выручку можно найти по формуле TR = Q∙P, где Q – объем продаж, а Р – цена товара. Для нахождения коэффициента эластичности необходимо воспользоваться формулой: , где Е_Р – коэффициент ценовой эластичности спроса.

	Товар А		Товар В		Товар С
Выручка, тыс. р.	400	360	100 000	150 000	10 000	10 000
Коэф. эласт.	– 7/11		– 1,5		– 1
Тип эластичности	Неэластичный спрос		Эластичный спрос		Единичная эластичность

Пример 6.

Цены на товар снизились на 15%, а объем спроса вырос с 200 ед. до 230 ед. Определите изменение выручки и сделайте вывод об эластичности спроса на товар.

Решение: Общую выручку можно найти по формуле TR = Q∙P, где Q – количество, а Р – цена товара. до изменения цены выручка составляла TR₁ = 200∙Р, а после изменения цены выручка стала равна TR₂ = 230∙0,85Р = 195,5∙Р.

Поскольку, при снижении цены выручка уменьшилась, спрос является неэластичным.

Ответ: неэластичный спрос.

Пример 7.

Цена товара увеличилась на 1% при эластичности спроса по цене, равной (-3). Как изменилась выручка продавца?

Решение: Общую выручку можно найти по формуле TR = Q∙P, где Q – количество, а Р – цена товара. Получаем, что до изменения цены выручка составляла TR₁ = Q∙Р, а после ее изменения выручка стала равна TR₂ = 0,97Q∙1,01Р = 0,98Q∙Р. Таким образом, выручка уменьшилась на 2%.

Ответ: уменьшилась на 2%.