Измерительные сигналы

Сигнал – физический процесс (или явление), несущий информацию о состоянии какого-либо объекта наблюдения. С точки зрения метрологии измерительным сигналом называется материальный носитель информации, представляющий собой некоторый физический процесс, один из параметров которого функционально связан с измеряемой физической величиной.

В метрологии измерительные сигналы являются в основном электрическими и описываются различными математическим моделями. Наиболее распространено временнóе и спектральное (частотное) представление и описание электрических сигналов.

Во временнóй области применяют определение функции времени , наиболее точно описывающие изменение сигнала (например, в виде напряжения), в которых один из параметров и т.д. зависит от измеряемой величины.

Спектральное представление электрических измерительных сигналов играет особую роль в процессе их генерации, передачи, приема и обработки, так как оно по существу определяет параметры и характеристики используемой аппаратуры.

Измерительные сигналы классифицируются по различным признакам и приведены ниже.

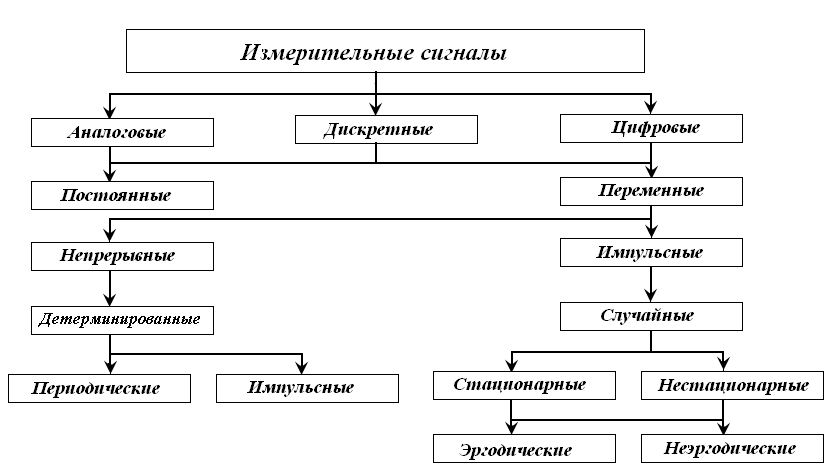
По характеру изменения информативного и временнóго параметров измерительные сигналы делятся на аналоговые, дискретные и цифровые.

Если физический процесс, порождающий сигнал, можно представить в виде непрерывной функции времени, то такой сигнал называют аналоговым (непрерывным).

Математическая модель дискретного сигнала – последовательность точек на временнóй оси, в каждой из которых заданы амплитудные значения соответствующего непрерывного сигнала. Эти значения называются выборками или отсчетами. Такие сигналы описываются решетчатыми функциями.

Цифровым называют сигнал с конечным числом дискретных уровней, поскольку уровни можно пронумеровать числами с конечным количеством разрядов.

В цифровом сигнале дискретные значения сигнала заменяются числами, чаще всего реализованными в двоичном коде, который представляют высоким (единица) и низким (нуль) уровнями потенциала напряжения.

По характеру изменения во времени измерительные сигналы делятся на постоянные, амплитуда которых с течением времени не изменяется, и переменные, мгновенные значения которых меняются во времени.

Переменные сигналы бывают непрерывными во времени и импульсными.

Непрерывный сигнал – сигнал, параметры которого изменяются во времени непрерывно.

Импульсный сигнал – сигнал с конечной энергией, существенно отличный от нуля в течение ограниченного интервала времени.

По математическому представлению (по степени наличия априорной информации) все измерительные сигналы делятся на две основные группы: детерминированные (регулярные) и случайные.

Детерминированными называют радиотехнические сигналы, мгновенные значения которых в любой момент времени достоверно известны, т.е. предсказуемы с вероятностью, равной единице. Детерминированными являются сигналы измерительных мер. Например, выходной сигнал генератора гармонических колебаний характеризуется значениями амплитуды, частоты и начальной фазы, которые установлены на его органах управления. Детерминированные сигналы бывают периодическими и импульсными.

Случайные сигналы – это сигналы, мгновенные значения которых в любой момент времени не известны и не могут быть предсказаны с вероятностью, равной единице.

Случайные сигналы делятся на стационарные и нестационарные.

Стационарными называют случайные сигналы, статистические характеристики которых не изменяются во времени.

Остальные случайные сигналы – нестационарные. Стационарные случайные сигналы бывают эргодическими и неэргодическими.

Практически все реальные радиотехнические случайные процессы относятся к стационарным. Подавляющее большинство случайных стационарных процессов обладают свойством эргодичности, при котором усреднение по ансамблю реализаций можно заменить усреднением по времени одной реализации в пределах бесконечно длинного интервала времени.

Проще говоря, для стационарного эргодического процесса любая его реализация является как бы «полномочным представителем» всей совокупности реализаций процесса.

В радиотехнике возможны и другие виды случайных процессов.

Стационарный неэргодический процесс – это случайный процесс, у которого вероятностные характеристики не зависят от времени, но зависят от номера реализации.

Нестационарный эргодический процесс – это случайный процесс, у которого вероятностные характеристики зависят от текущего времени, но не зависят от номера реализации.

Нестационарный неэргодический процесс – это процесс, у которого не эквивалентны ни временные сечения, ни реализации.