2.6. Методы решения задач на вычисление углов

Рассмотрим основные методы решения задач на нахождение углов на примере задачи 18.

Задача 18. Дан равнобедренный треугольник АВС с прямым углом С и гипотенузой, равной . Через вершину С проведена прямая CD, перпендикулярная плоскости АВС, CD=1. Точки М и N – середины отрезков АС и АВ соответственно. Найти углы между а) прямыми DM и CN; б) прямой DN и плоскостью BCD; в) плоскостями ABD и ABC; г) плоскостями ABD и CBD.

Синтетический (конструктивный) метод

При вычислении угла в пространстве можно

1. построить (изобразить) или найти (если есть на рисунке) искомый угол согласно определению;

2. выбрать треугольник, одним из углов которого является искомый угол или дополняющий его до 180°;

3. найти этот угол из треугольника (если треугольник прямоугольный, то используются свойства его острых углов или определения синуса, косинуса или тангенса; если же треугольник непрямоугольный, то используются теоремы косинусов, синусов и другие теоремы планиметрии);

4. найти искомый угол;

5. записать ответ.

Такой метод нахождения углов называют синтетическим, поскольку при решении используются определения и теоремы синтетической геометрии. Его также называют конструктивным, т.к. он основан на построении, конструировании определенных фигур, часто – на дополнительных построениях.

Решим синтетическим методом задачу 18.

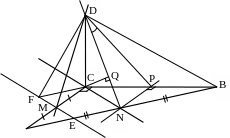
A

Рис. 28

Решение.

а) Проведем через точку М прямую, параллельную прямой CN. Она пересечет АВ в точке Е (рис. 28). Тогда (DM,CN) = (DM,ME) по определению угла между скрещивающимися прямыми.

Нетрудно установить, что CN=NA=NB= CA=CB=2, ME= CN= AE=EN= CM=MA=1.

Получили треугольник DME, в котором угол DME дополняет угол между прямыми DM и МЕ до 180°. DM можно найти из треугольника DCM, DE – из треугольника DNE, где DN – гипотенуза прямоугольного треугольника DCN с известными катетами. Таким образом, из треугольника DME можно найти угол DME, используя теорему косинусов, а затем искомый угол.

Поступим иначе. Проведем через точку С прямую CF (F МЕ), параллельную АВ. Получим прямоугольный треугольник DFM, в котором угол DMF – искомый. Четырехугольник FCNE – параллелограмм по определению, и угол CNE у него прямой, следовательно, это прямоугольник; по теореме о трех перпендикулярах, следовательно, . Из треугольника DCM найдем , а Тогда cos и значит, ( ) = 60°.

Во втором способе решения фактически выполнен параллельный перенос отрезка CN на вектор NE. Такой прием часто используется при нахождении угла между скрещивающимися прямыми в тех случаях, когда прямые задаются отрезками – элементами известных фигур.

б) Так как прямая CD перпендикулярна плоскости ABC, то любая прямая плоскости АВС перпендикулярна прямой CD. Проведем в этой плоскости прямую NP перпендикулярную прямой CВ. Тогда прямая NP перпендикулярна плоскости BCD (по признаку) и DP – проекция DN на плоскость BCD (рис.28). Следовательно, - искомый угол.

В треугольнике NPD имеем: , sin arcsin Значит, (DN,BCD)=arcsin

в) Построим линейный угол двугранного угла DABC: как медиана равнобедренного треугольника с основанием АВ, по теореме о трех перпендикулярах, - искомый. Так как - не прямой угол прямоугольного треугольника, то он острый. Следовательно,

Найдем величину угла из прямоугольного треугольника : cos (ABD,ABC)=arccos arcsin

г) Угол между плоскостями ABD и CBD можно найти через двугранный угол ABCD. Однако построить линейный угол этого двугранного угла не так просто, как в предыдущем случае, еще сложнее найти его величину. Поэтому будем находить угол между прямыми, перпендикулярными плоскостям.

Так как и угол АСВ прямой, то и то есть (рис. 28).

Из и следует, что , и значит, любая прямая плоскости CND перпендикулярна прямой АВ. Проведем , тогда по признаку перпендикулярности прямой и плоскости.

Таким образом, (ABD,CBD) = (CA,CQ).

Рассмотрим треугольник ACQ и найдем из него угол ACQ. Для этого потребуется найти длины отрезков CQ и AQ.

Отрезок CQ – высота, проведенная к гипотенузе треугольника DCN. Вычисляя площадь треугольника DCN двумя способами, получим равенство из которого

Из треугольника CQN найдем Из прямоугольного треугольника AQN

По следствию из теоремы косинусов для треугольника ACQ получим: cos или cos arccos

Таким образом, (ABD,CBD)= (CA,CQ)=arccos

Ответ. а) 60°; б) arcsin ; в) arcsin ; г) arccos