
- •Высшего профессионального образования
- •Введение
- •Примерный тематический план изучения темы
- •Требования к знаниям и умениям студентов
- •§ 1. Вычисление расстояний в курсе стереометрии
- •1.1. Различные виды расстояний в пространстве
- •1.2. Вычисление расстояния от точки до прямой
- •1.3. Вычисление расстояния от точки до плоскости
- •1. 4. Расстояние между скрещивающимися прямыми
- •Задачи для самостоятельного решения
- •§ 2. Вычисление углов в курсе стереометрии
- •2.1. Угол между лучами
- •2.2. Угол между прямыми
- •2.3. Угол между прямой и плоскостью
- •2.4. Двугранный угол
- •2.5. Угол между плоскостями
- •2.6. Методы решения задач на вычисление углов
- •Аналитические методы
- •Задачи для самостоятельного решения
- •Контрольная работа
- •Список литературы
- •Содержание
- •§1. Вычисление расстояний в курсе стереометрии………………………6
- •§2. Вычисление углов в курсе стереометрии……………………………..27
- •603950, Нижний Новгород, гсп-37, ул. Ульянова, 1
2.1. Угол между лучами
Любые два луча в пространстве либо имеют общее начало, либо их начала – разные точки. Лучи с разными началами могут лежать на одной прямой, на параллельных или на скрещивающихся прямых. Определение понятия угла между лучами для общего случая опирается на понятие сонаправленных лучей. Поэтому определим сначала понятие «сонаправленные лучи».
Два луча называются сонаправленными (одинаково направленными), если либо один из них содержит другой (пересечением лучей является один из них), либо они лежат на параллельных прямых в одной полуплоскости относительно прямой, содержащей начала лучей (рис. 20, а, б).
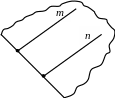
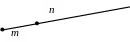
а) б)
Рис. 20
Угол между сонаправленными лучами считается равным 0°.
Если лучи т и п не сонаправлены и имеют общее начало, то углом между ними называется величина (мера) плоского выпуклого угла (т.е. не большего 180°) со сторонами т и п (рис.21).
Если лучи т и п не сонаправлены и имеют различные начала, то углом между ними называется угол между лучами т´ и п´, соответственно сонаправленными с лучами т и п и имеющими общее начало (рис.22). Нетрудно доказать, что величина этого угла не зависит от выбора точки О – начала лучей, сонаправленных с лучами т и п.
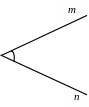
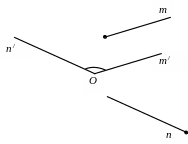
Рис. 21 Рис. 22
Таким образом, угол между лучами принимает значения от 0° до 180°.
Угол между лучами т и п будем обозначать так: (m,n).
2.2. Угол между прямыми
Две пересекающиеся прямые определяют на плоскости, содержащей эти прямые, четыре угла с общей вершиной. Если величина одного из них равна φ, то остальные три угла равны 180°-φ, φ и 180°- φ. Если один из углов прямой (равен 90°), то и остальные три угла прямые.
Углом между двумя пересекающимися прямыми называется величина плоского угла, не превосходящая величины каждого из остальных углов, образовавшихся при пересечении прямых.
Две пересекающиеся прямые называются перпендикулярными, если угол между ними равен 90°.
У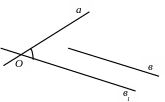 глом
между скрещивающимися прямыми называется
угол
между пересекающимися прямыми,
соответственно параллельным данным
скрещивающимся прямым.
глом
между скрещивающимися прямыми называется
угол
между пересекающимися прямыми,
соответственно параллельным данным
скрещивающимся прямым.
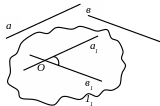
Рис. 23 Рис. 24
Другими словами, чтобы найти угол между скрещивающимися прямыми а и в, нужно через произвольную точку пространства провести прямые а1||а и в1||в. Угол между прямыми а и в равен углу между прямыми а1 и в1 (рис. 23). Он не зависит от выбора точки, через которую проводят прямые а1 и в1. При решении задач часто выбирают точку на одной прямой и через нее проводят прямую, параллельную другой прямой (рис. 24).
Угол между двумя прямыми можно определить также следующим образом: углом между прямыми называется небольший из двух углов между лучами, параллельными этим прямым.
Из вышесказанного следует, что угол между прямыми в пространстве есть величина, принадлежащая отрезку [0°; 90°].
Угол между прямыми будем обозначать так: (а,в).
