1. 4. Расстояние между скрещивающимися прямыми

Сначала докажем существование общего перпендикуляра двух скрещивающихся прямых.

Пусть даны две скрещивающиеся прямые а и b. Построим плоскость , которая содержит прямую b и параллельна прямой a (рис. 6). Далее ортогонально спроектируем прямую а на плоскость . Допустим, что получим прямую а_1. Прямые а₁ и b являются пересекающимися (попытайтесь доказать этот факт самостоятельно). Пусть точка О₁ есть точка пересечения прямых а₁ и b. Далее построим точку О, лежащую на прямой а, для которой точка О₁ является ортогональной проекцией.

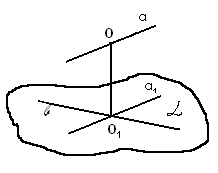
Рис. 6

Из построений следует, что отрезок ОО₁ перпендикулярен плоскости . Следовательно, он перпендикулярен прямым а₁ и b. В силу параллельности прямых а и а₁ получаем, что ОО₁  а.

Таким образом, отрезок ОО₁ является общим перпендикуляром двух скрещивающихся прямых а и b.

Итак, мы доказали существование общего перпендикуляра скрещивающихся прямых. Попытайтесь самостоятельно доказать его единственность.

Приведенное доказательство позволяет выделить следующие способы нахождения расстояния между скрещивающимися прямыми:

1 способ. Непосредственно построить общий перпендикуляр скрещивающихся прямых и найти его длину;

2 способ. Через одну из скрещивающихся прямых провести плоскость, параллельную другой прямой, и найти расстояние от этой прямой до параллельной плоскости;

3 способ. Построить пару параллельных плоскостей, каждая из которых содержит одну из скрещивающихся прямых, и найти расстояние между параллельными плоскостями.

4 способ. На основе второго способа можно получить еще один способ нахождения расстояния между скрещивающимися прямыми.

Пусть а и b – скрещивающиеся прямые (рис. 7). Построим плоскость β, перпендикулярную прямой а, и спроектируем ортогонально на плоскость β прямую b. Пусть эта проекция есть прямая b₁. Очевидно, что плоскость γ, проходящая через прямые b и b₁, параллельна прямой а. Следовательно, если точка А – точка пересечения прямой а с плоскостью β, то расстояние между данными прямыми равно расстоянию от точки А до прямой b₁.

Заметим, что описанные выше способы относятся к конструктивному методу решения соответствующих задач. Проиллюстрируем их при решении задач на вычисление расстояния между скрещивающимися прямыми на элементах куба.

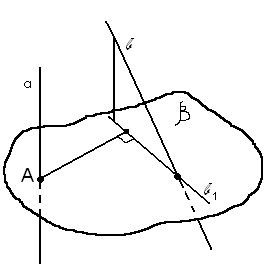
Рис. 7

Задача 4. Найдите расстояние между двумя скрещивающимися прямыми, каждая из которых содержит ребро куба, равное а.

Решение

Пусть данными прямыми являются прямые АВ и СС₁ (рис. 8). Очевидно,

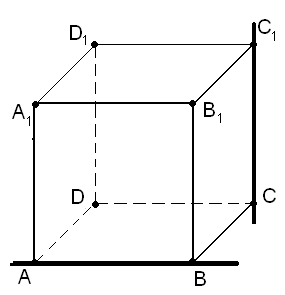
Рис. 8

что отрезок ВС является общим перпендикуляром этих прямых. Следовательно,  (АВ, СС₁) = а.

Ответ. а.

Задача 5. Найдите расстояние между двумя скрещивающимися прямыми, одна из которых содержит ребро куба длины а, а другая – диагональ его грани.

Решение

Задача сводится к рассмотрению двух случаев: одна из скрещивающихся прямых содержит ребро куба, а другая – диагональ смежной грани или диагональ противоположной грани.

1 случай

Пусть даны скрещивающиеся прямые C₁D₁ и В₁С. Легко убедиться, что отрезок В₁С₁ не является общим перпендикуляром данных скрещивающихся прямых (рис. 9). Однако плоскость В₁С₁С перпендикулярна прямой C₁D₁. Следовательно, любая прямая этой плоскости перпендикулярна прямой C₁D₁, в том числе и прямая, проходящая через вершину C₁ и перпендикулярная В₁С, то есть прямая ВC₁. Значит,  (C₁D₁, В₁С) = C₁М = .

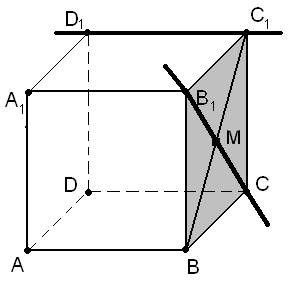
Рис. 9

2 случай

Пусть даны скрещивающиеся прямые C₁D₁ и А₁В (рис. 10). Тогда очевидно,

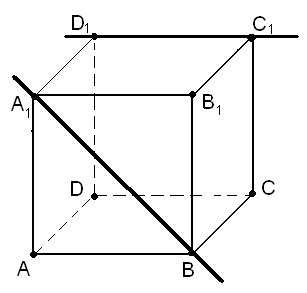
Рис. 10

что отрезок А₁D₁ является общим перпендикуляром прямых C₁D₁ и А₁В. Значит,  (C₁D₁, А₁В) = а.

Ответ. или а.

Задача 6. Найдите расстояние между двумя скрещивающимися прямыми, каждая из которых содержит диагональ грани куба с ребром а.

Решение

1 случай

Диагонали расположены в противоположных гранях (рис. 11).

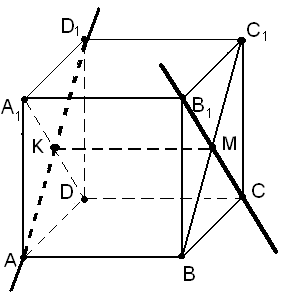
Рис. 11

Пусть это будут диагонали АD₁ и B₁C_. Нетрудно доказать, что отрезок КМ является общим перпендикуляром прямых АD₁ и В₁С, где точки К и М – середины соответственно диагоналей AD₁ и В₁С.

Можно решить эту задачу с опорой на 2-ой или 3-ий вышеуказанные способы, то есть свести задачу к нахождению расстояния между: а) прямой В₁С и параллельной ей плоскости DAA₁, в которой лежит другая скрещивающаяся прямая AD₁; б) параллельными плоскостями ВСС₁ и DAA₁, в каждой из которых лежат соответственно скрещивающиеся прямые В₁С и AD₁.

2 случай. Диагонали расположены в смежных гранях куба, например, АВ₁ и ВС₁ (рис. 12).

Обнаружить быстро общий перпендикуляр данных прямых, как это было сделано при решении предыдущих задач, здесь не удается. Однако легко убедиться в том, что ВС₁ (АВ₁D₁). Тогда нужно найти расстояние от прямой ВС₁ до указанной плоскости_. Для этого на прямой ВС₁ следует выбрать некоторую точку и построить перпендикуляр к плоскости АВ₁D₁. Из какой точки удобнее построить перпендикуляр? Интуиция, пространственное воображение ведут к избранию точки С₁. Возникает вопрос: где расположено основание Е перпендикуляра? Вот если бы удалось выявить плоскость, проходящую через точку С₁ и перпендикулярную плоскости АВ₁D₁, то ответ на поставленный вопрос значительно бы упростился, так как точка Е принадлежит прямой пересечения указанных плоскостей.

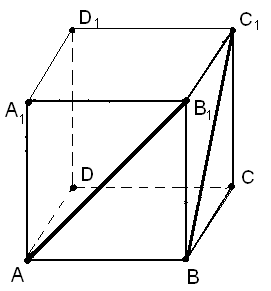
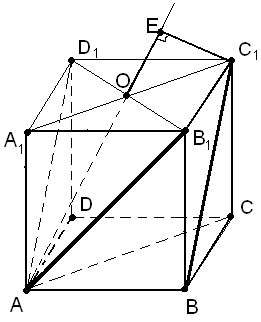
Рис. 12 Рис. 13

Начинаем поиск такой плоскости. И снова выручают интуиция и пространственное воображение. По-видимому, (АА₁С)  (АВ₁D₁). Если это так, то основание Е перпендикуляра принадлежит прямой АО (рис. 13). Тогда проведем С₁Е  АО. Однако надо еще доказать перпендикулярность названных плоскостей. Видимо, нужно воспользоваться признаком перпендикулярности двух плоскостей. Это означает, что надо установить: одна из двух интересующих нас плоскостей проходит через прямую, перпендикулярную другой плоскости. Кажется, B₁D₁  (АА₁С₁). Почему? Возможны различные способы доказательства последнего факта.

1. Точки А, А₁, С равноудалены от концов отрезка В₁D₁. Следовательно, они принадлежат множеству точек пространства, равноудаленных от концов названного отрезка, то есть лежат в плоскости, перпендикулярной отрезку В₁D₁ и проходящей через его середину. Но такой плоскостью является плоскость АА₁С₁.

2. В₁D₁  A₁C₁, как диагонали квадрата, и В₁D₁  АО по теореме о трех перпендикулярах. Следовательно, В₁D₁  (АА₁С₁).

3) В₁D₁  A₁C₁ и АА₁  В₁D₁, так как АА₁  (А₁В₁С₁). Следовательно, В₁D₁  (АА₁С₁).

Итак, (АА₁С₁)  (АВ₁D₁), где АО – линия пересечения этих плоскостей. Исходя из вышеприведенных рассуждений, строим С₁Е  АО. Следовательно, задача свелась к поиску длины отрезка С₁Е. В плоскости АА₁С₁ имеем два подобных треугольника АА₁О₁ и С₁ЕО. Отсюда получаем С₁Е = .

Таким образом, расстояние между скрещивающимися прямыми ВС₁ и АВ₁ есть длина перпендикуляра, проведенного из некоторой точки С₁ одной из скрещивающихся прямых ВС₁ к плоскости, содержащей другую скрещивающуюся прямую АВ₁ и параллельную первой прямой ВС₁.

При решении задачи мы строили перпендикуляр из точки С₁. Однако на выбор некоторой точки прямой ВС₁ претендовала и точка В. Попытайтесь построить перпендикуляр из точки В к плоскости АВ₁D₁. Такое решение будет нерациональным, но зато очень полезным в математическом отношении.

«Поменяйте ролями» прямые АВ₁ и ВС₁. Проведите через вторую из них плоскость, параллельную первой. В этом случае надо искать расстояние от прямой АВ₁ до плоскости ВDС₁. Здесь перпендикуляр можно строить из точек А или В₁ к плоскости ВDС₁.

Таким образом, мы выявили четыре варианта решения одной и той же задачи, построенных на одной идее – втором способе нахождения расстояния между скрещивающимися прямыми.

Перейдем к рассмотрению еще одного способа отыскания расстояния между скрещивающимися прямыми АВ₁ и ВС₁.

Плоскости АВ₁D₁ и ВС₁D параллельны и проходят через скрещивающиеся прямые АВ₁ и ВС₁ (рис. 14). Надо найти расстояние между этими плоскостями.

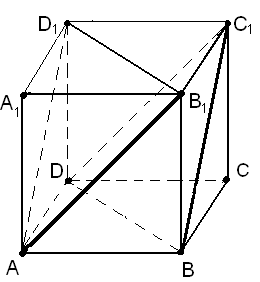
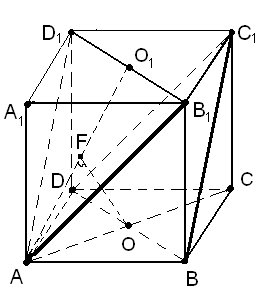
Рис. 14 Рис. 15

Из какой точки одной плоскости удобно провести перпендикуляр к другой? По-видимому, из точек О или О₁ – середин отрезков ВD и B₁D₁ (рис. 15). Пусть мы выбрали для определенности точку О. Где же лежит основание перпендикуляра, проведенного из точки О к плоскости АВ₁D₁? Скорее всего, на прямой АО₁. Почему? В силу перпендикулярности прямой В₁D₁ к плоскости АА₁С₁. Поэтому (АВ₁D₁)  (АА₁С₁). Прямая АО₁ – линия пересечения этих плоскостей. Проведя ОF  АО₁, получим ОF  (АВ₁D₁).

Из прямоугольного треугольника АОF имеем: ОF = АО  sinОАF = = = .

Заметим, что вычисление расстояния между параллельными плоскостями АВ₁D₁ и ВC₁D намного упростится, если использовать свойство диагонали куба А₁С о перпендикулярности этим плоскостям. В этом нетрудно убедиться.

Действительно, ортогональной проекцией А₁С на плоскость А₁В₁В является прямая А₁В (рис. 15). Значит, по теореме о трех перпендикулярах имеем: А₁С  АВ₁. Аналогично можно доказать, что прямая АС₁ перпендикулярна В₁D₁ (или АD₁). Поэтому на основании признака перпендикулярности прямой и плоскости делаем вывод: А₁С  (АВ₁D₁). Таким же образом или используя свойство параллельных плоскостей АВ₁D₁ и ВС₁D, можно доказать, что А₁С  (ВС₁D).

Далее построим точки пересечения диагонали А₁С с этими плоскостями, как точки пересечения А₁С с прямыми АО₁ и С₁О, которые, с одной стороны, лежат соответственно в плоскостях АВ₁D₁ и ВС₁D, а с другой стороны, в одной плоскости с прямой АС₁ (рис. 16). Пусть это будут точки М и N. Следовательно, задача свелась к вычислению длины отрезка МN в плоскости А₁С₁СА.

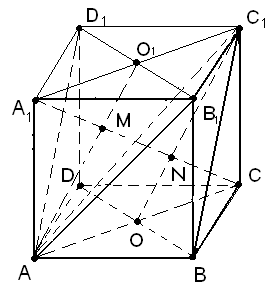
Рис. 16

Итак, имеем классическую задачу из курса планиметрии.

Дан параллелограмм АА₁С₁С, точки О и О₁ – соответственно середины его сторон АС и А₁С_1. Доказать, что точки пересечения отрезков АО₁ и С₁О с диагональю А₁С делят ее на три равные части (рис 17).

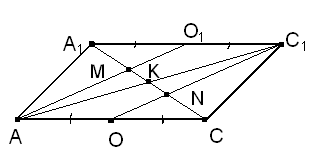
Рис. 17

Решение

Выполним дополнительное построение: проведем вторую диагональ АС₁ данного параллелограмма. Используя свойство медиан треугольника, имеем: А₁М = 2 МК, СN = 2 КN. Учитывая свойство диагоналей параллелограмма, получаем: А₁К = КС. Значит, А₁М = МN= NС.

Опираясь на результат этой задачи, делаем вывод о том, что расстояние между параллельными плоскостями АВ₁D₁ и ВС₁D равно одной трети длины диагонали куба, то есть .

Ответ. Расстояние между скрещивающимися прямыми, которые содержат диагонали противоположных граней, равно а. Расстояние между скрещивающимися прямыми, которые содержат диагонали смежных граней, равно .

Попытаемся теперь решить последнюю задачу (2 случай) аналитическими методами.

Векторный метод

Введем базисные векторы: = , ВВ₁ = , ВС = (рис. 18).

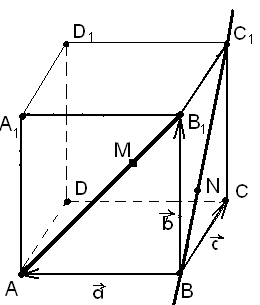
Рис. 18

Известно, что две скрещивающиеся прямые имеют общий перпендикуляр и притом единственный. Допустим, что это есть отрезок MN, где МАВ₁, NBC₁. Следовательно, MN  АВ₁ и MN  ВС₁. Переведем последние четыре факта на векторный язык:

МАВ₁ = х , NВС₁ = у ,

MN  АВ₁ · = 0, (1) MN BC₁ · = 0. (2)

Затем выразим записанные векторы через базисные:

– = х ( - ) = (1 – х) + х ;

= у ( + );

= – = у ( + ) – (1 – х) – х = (x – 1) + (y – x) + у .

Дальнейший ход рассуждений таков: сначала вычислим коэффициенты

разложения вектора по базисным векторам , и , используя векторные равенства (1) и (2). Потом найдем его скалярный квадрат, что и позволит вычислить длину отрезка MN. Исходя из этого плана, запишем:

((х – 1) + (y – x) + y )  ( – ) = 0;

((х – 1) + (y – x) + y )  ( + ) = 0.

П рименяя законы векторной алгебры и свойства куба, имеем:

(y-x)a² – (x-1)a² = 0,

(y-x)a² + уа² = 0.

Значит,

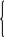
у = 2х – 1, х = ,

2у = х;  у = .

Следовательно, = – – – .

Отсюда MN = а = .

Ответ. Расстояние между скрещивающимися прямыми, которые содержат диагонали смежных граней, равно .

Координатно-векторный метод

Введем прямоугольную систему координат (рис. 19). Запишем координаты следующих точек: А(а, 0, 0), В(0, 0, 0), В₁(0, 0, а), С(0, а, 0), С₁(0, а, а). Допустим, что отрезок MN (МАВ₁ и NВC₁) является общим перпендикуляром скрещивающихся прямых АВ₁ и ВС₁. Дальнейшая идея решения заключается в нахождении координат точек М и N, что позволит вычислить длину отрезка MN.

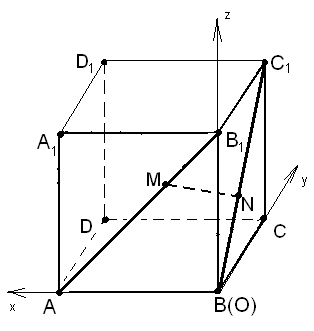
Рис. 19

Имеем, что точки А, М и В₁ лежат на одной прямой, что соответствует векторному равенству = х . Исходя из этого равенства, найдем координаты точки М. Заметим, что точка М лежит в плоскости Охz. Следовательно, она имеет координаты вида (m, 0, n). Тогда можно определить координаты следующих векторов: (m-n; 0; n), (-а; 0; а), х (-ха; 0; ха). Отсюда выражаем координаты точки М(а-ах; 0; ах).

Аналогично N = y N (0; ау; ау). Следовательно, (ах- а; ау; ау - ах).

Чтобы найти числовые значения х и у, воспользуемся условиями перпендикулярности отрезка MN к прямым АВ₁ и ВС₁:

 = 0 (ax - a)  (-a) + ay  0 + (ay – ax)  a = 0;

 = 0 (ax - a)  0 + ay  a + (ay - ax)  a = 0.

Разделив обе части равенств на а² (по условию задачи а0), получаем:

1 – х + у – х = 0,

у + (у - х) = 0.

Отсюда х = , у = Значит, М( , 0, ) и N(0, , ).

Итак, MN = = .

Ответ. .

Заметим, что по окончании решения задачи с помощью векторов и координат, мы можем построить непосредственно точки М и N (точка М делит отрезок АВ₁ в отношении 2:1, начиная от вершины А, а точка N делит отрезок ВС₁ в отношении 1:2, начиная от вершины В), а значит, и общий перпендикуляр данных прямых.