Задачи для самостоятельного решения
19. Основанием пирамиды PABCD является квадрат. Ребро РВ перпендикулярно основанию и равно стороне квадрата. Вычислите угол между а) прямыми PD и АВ; б) прямой PD и плоскостью APC; в) прямой AD и плоскостью PCD; г) плоскостями РАВ и РСD; д) плоскостями PAD и PCD.
20. В кубе ABCDA1B1C1D1 найдите угол между прямой АВ1 и плоскостью АВС1 .
21.
Основанием прямой четырехугольной
призмы ABCDA1B1C1D1
служит прямоугольник ABCD,
в котором АВ=3,
AD=
Найдите угол между плоскостью AA1D1
и
плоскостью, проходящей через середину
ребра CD
перпендикулярно прямой B1D,
если расстояние между прямыми А1С1
и ВD
равно
22.
В правильном треугольнике АВС
сторона равна а.
На сонаправленных лучах BD
и CE,
перпендикулярных к плоскости АВС,
взяты точки D
и Е
так, что
Найдите
угол между а) DA
и DE;
б) АВС
и АDЕ.
23. С началом в точке А проведены четыре луча АВ, АС, АD, АЕ так, что BAC=60°, BAD = DAC=45°, а луч АЕ перпендикулярен к плоскости АВD. Найдите угол САЕ.
24. Дан куб ABCDA1B1C1D1, точки М и N – середины ребер A1D1 и СС1 соответственно. Найдите угол между плоскостями BMN и АВС.
25. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 ребро основания равно 1, а боковое ребро – 3. Найдите угол между прямой ВА1 и плоскостью АВС1.
26. В тетраэдре ABCD грань ABC – правильный треугольник. Грань DВС перпендикулярна плоскости АВС, а две оставшиеся грани составляют с гранью DВС угол φ. Чему равен угол между а) DА и ВС; б) DВ и АС; в) DА и АВС; г) DАВ и DАС; д) DАС и DВС?
27. В сфере проведен диаметр SB. Через точку S проведены хорды SA и SC так, что ASB= CSB=45°, ASC=60°. Найдите угол между а) плоскостями АВС и ASС; б) плоскостями АВС и ASB; в) плоскостями ASB и ВSС; г) прямой AS и плоскостью ВSС; д) прямыми SС и АВ.
28.
В основании пирамиды МАВС
лежит равносторонний треугольник АВС,
длина стороны которого равна
Боковое
ребро МС
перпендикулярно плоскости основания
и имеет длину 2. Найдите расстояние и
угол между прямыми МР
и СQ,
где точки Р
и Q
– середины ребер ВС
и АВ
соответственно.
29. Дан куб ABCDA1B1C1D1 с ребром, равным а. Точка К – середина ребра A1D1. Найдите а) расстояние между прямыми ВК и СВ1; б) угол между прямыми BK и CB1; в) угол между прямой ВК и плоскостью АВС.
30. Найдите расстояние и угол между двумя скрещивающимися медианами граней тетраэдра, каждое ребро которого равно 1. (Исследуйте все возможные расположения медиан).
Контрольная работа
Основанием пирамиды FАВС является треугольник АВС, в котором АВС = 900, АВ = 3, ВС = 4. Ребро АF перпендикулярно плоскости АВС и равно 4.
1. Найдите расстояния:
а) от точки А до плоскости ВСF;
б) от середины отрезка СF до прямой ВC;
б) между прямыми ВF и АС.
2. Вычислите углы:
а) (FВ, АCF);
б) (АCF; ВСF).
Ответы
7. d – (R1 +R2).
8.
а) 2; б) 2; в) 2; г) 2; д)
/2;
е)
;
ж)
;
з) 2
/5;
и)
;
к)
/2;
л)
.
9.
а) а
/12;
б) а
/2;
в) а
/6.
10.
а) 2
;
б) 3
/2.
11.
а) аsinαtgβ/(1
+ sin
);
б)
а
sin2α
tgβ.
12.
и
sin
.
13.
2,5. 14.
.
15.
.
16.
.
17.
а
/3.
а) arccos
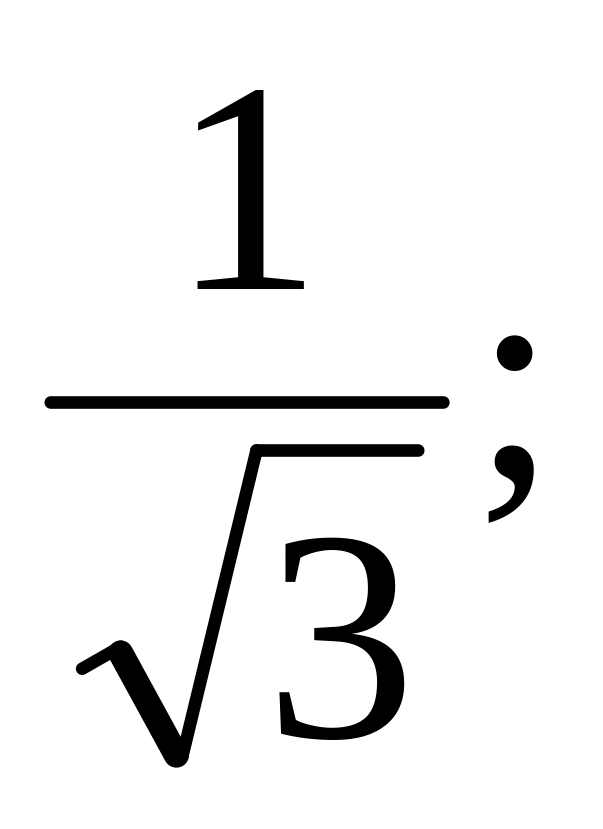б) arccos
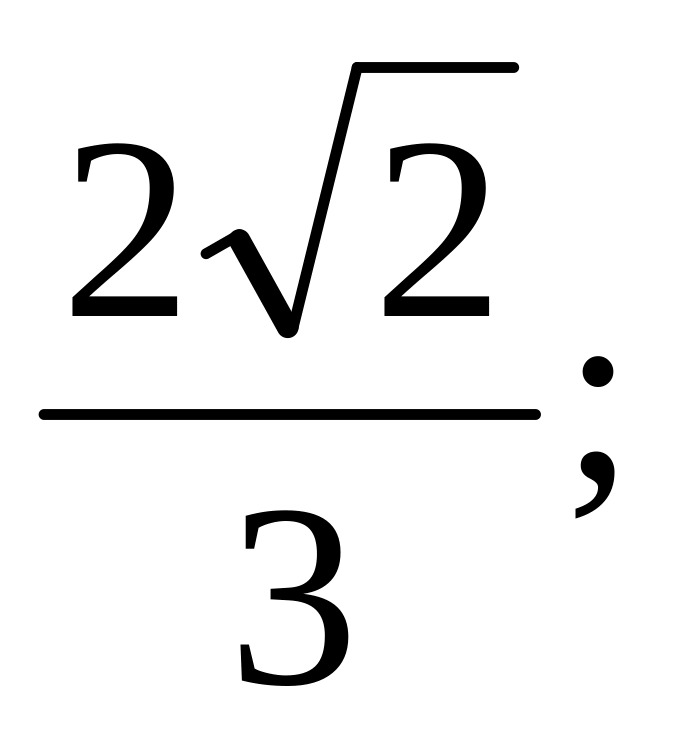в) 45°; г) 45°; д) 120°.
20.
30°. 21.
arctg
22.
а) 90°; б) arccos
23.
45° или 135°.
24.
arccos
25.
arcsin
26.
а)
90°; б)
arctg
в)
arctg(
tg
φ);
г)
arccos
д) arccos
27.
а) arccos
б) arctg
в) 90°; г) 45°; д) 60°.
28.
45°. 29. а)
б) arccos
в) arcsin
30.
arccos
arccos