Аналитические методы

Векторный метод

Для вычисления углов во многих случаях удобно использовать скалярное произведение векторов.

Пусть и - два вектора. Отложим от какой-нибудь точки О векторы Если векторы и не сонаправлены, то лучи ОА и ОВ образуют угол АОВ. Градусная мера угла АОВ называется углом между векторами и . Если векторы и сонаправлены, в частности один из них или оба нулевые, то считается, что угол между ними равен 0°. Если угол между векторами равен 90°, то векторы называются перпендикулярными.

Угол между векторами и обозначают ( ). Очевидно, что 0°≤ ( )≤180°.

Пусть теперь h и k – два луча. Рассмотрим ненулевые векторы и соответственно сонаправленные с лучами h и k. Тогда (h,k)= ( ) и cos (h,k)=cos ( )= (1)

Ненулевой вектор называется направляющим вектором прямой а, если он лежит либо на прямой а, либо на прямой, параллельной а.

Выясним, как можно найти угол между прямыми а и в с помощью векторов.

Пусть - направляющие векторы прямых а и в соответственно. Введем обозначения: (а,в) = φ, ( ) = θ.

Если 0° ≤ θ ≤ 90°, то φ = θ и cosφ = cosθ = |cosθ|, т.к. cosθ ≥ 0.

Если же 90° < θ ≤ 180°, то φ = 180° - θ и cosφ = -cosθ.

Так как 90° < θ ≤ 180°, то cosθ < 0, а –cosθ > 0, т.е. cosφ = |cosθ|.

Таким образом, получим: cos (а,в) = |cos ( )| = (2)

где - направляющие векторы прямых а и в соответственно.

Выясним, как найти с помощью векторов угол между прямой и плоскостью.

Пусть - направляющий вектор прямой а, - ненулевой вектор, перпендикулярный к плоскости α. Обозначим углы: (а,α) = φ, = θ. В зависимости от выбора векторов и могут представиться два случая (рис. 29, а, б).

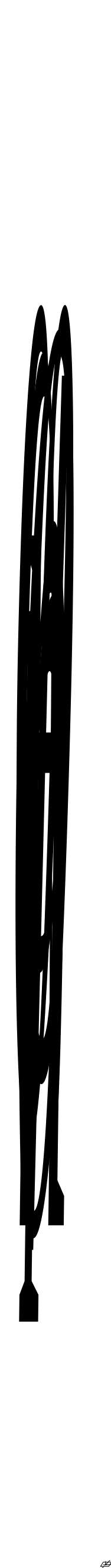
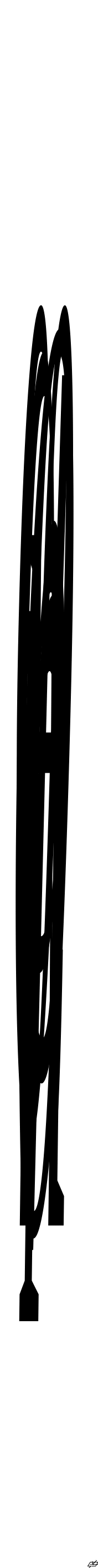
а) б)

Рис. 29

Если 0° ≤ θ ≤90° (рис. 29, а), то φ = 90° - θ, θ = 90° - φ, cosθ = sinφ. Если 90° < θ ≤ 180°, то φ = θ - 90°, θ = 90° + φ, cosθ = -sinφ, sinφ = -cosθ = |cosθ|, т.к. cosθ <0, а -cosθ>0.

Итак получим sin (a,α) = |cos | = (3)

где - направляющий вектор прямой а, - вектор, перпендикулярный плоскости α.

Так как угол между плоскостями равен углу между прямыми, перпендикулярными этим плоскостям, то

cos (α,β) = |cos ( )| = (4)

где - векторы, перпендикулярные плоскостям α и β соответственно (направляющие векторы прямых, перпендикулярных плоскостям α и β).

Имея формулы (1)-(4), при нахождении угла в пространстве можно поступить следующим образом:

1. ввести базисные векторы;

2. выбрать нужную из формул (1)-(4);

3. выразить векторы, входящие в формулу, через базисные;

4. подставить найденные выражения в формулу и произвести вычисления;

5. записать ответ.

Подчеркнем, что базис в пространстве - это тройка некомпланарных векторов, для которых известны длины и углы между каждыми двумя векторами. Для нахождения углов достаточно знать не длины векторов, а отношения длин.

Такой метод нахождения углов называется векторным.

Решим векторным методом задачу 18.

Решение. Выберем в качестве базисных векторы = При этом = (рис.30).

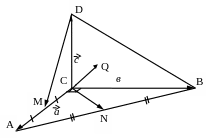
Рис. 30

а) и - направляющие векторы прямых DM и CN. Выразим эти векторы через базисные: .

сos (DM,CN) = |cos ( , )| =

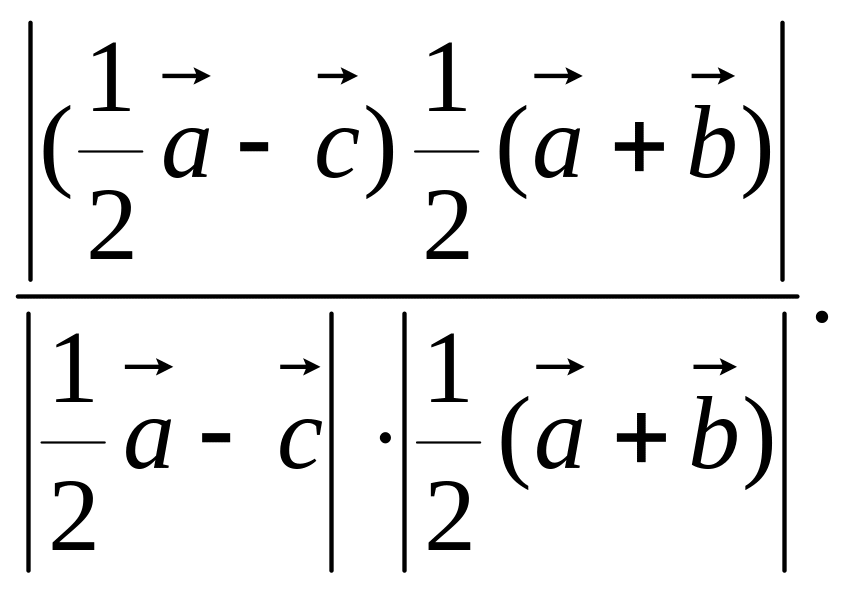
Подсчитаем отдельно значения выражений в числителе и знаменателе:

Подставим найденные значения в формулу: cos (DM,CN)= Тогда (DM,CN)=60°.

Заметим, что длины векторов DM и CN можно было найти и синтетическим методом: DM из треугольника DCM, CN – медиана, проведенная к гипотенузе в прямоугольном треугольнике, CN= АВ.

б) Для нахождения угла между прямой DN и плоскостью ВСD воспользуемся формулой (3), учитывая, что плоскости ВСD перпендикулярен вектор

sin (DN,BCD) = |cos ( )| = .

Выразим вектор через базисные и произведем необходимые вычисления:

sin (DN,BCD) =

(DN,BCD) = arcsin

в) Угол между плоскостями находится по формуле (4). Плоскости АВС перпендикулярен вектор Пусть вектор перпендикулярен плоскости АВD. Разложим его по базисным векторам.

Так как точка Q принадлежит плоскости АВD, то Здесь х и у неизвестны.

Из перпендикулярности вектора плоскости АВD следует, что, например, вектор перпендикулярен векторам Тогда имеем систему

Подставляя в уравнения системы выражения векторов через базисные и произведя вычисления, получим систему двух алгебраических уравнений с двумя неизвестными:

Тогда

и cos (АВС,АВD)=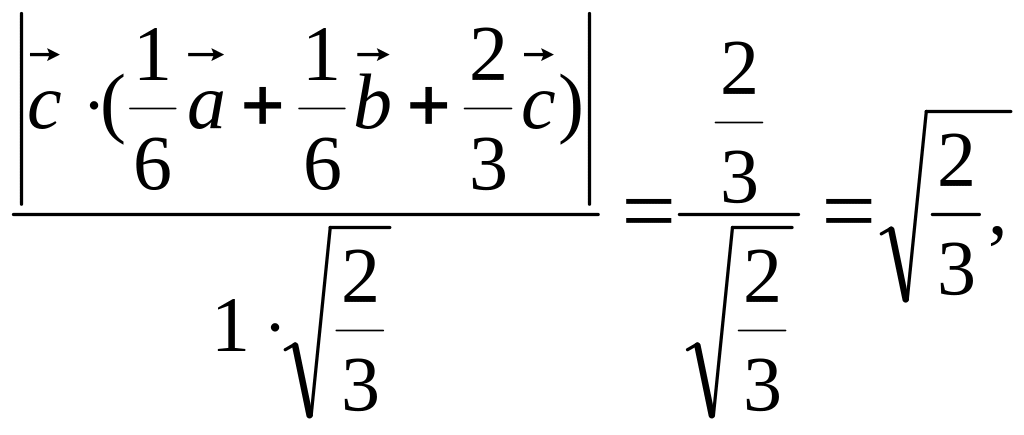 (АВС,АВD) = arccos

г) Для нахождения угла между плоскостями АВD и СВD все подготовлено:

cos (ABD,CBD) = |cos | =

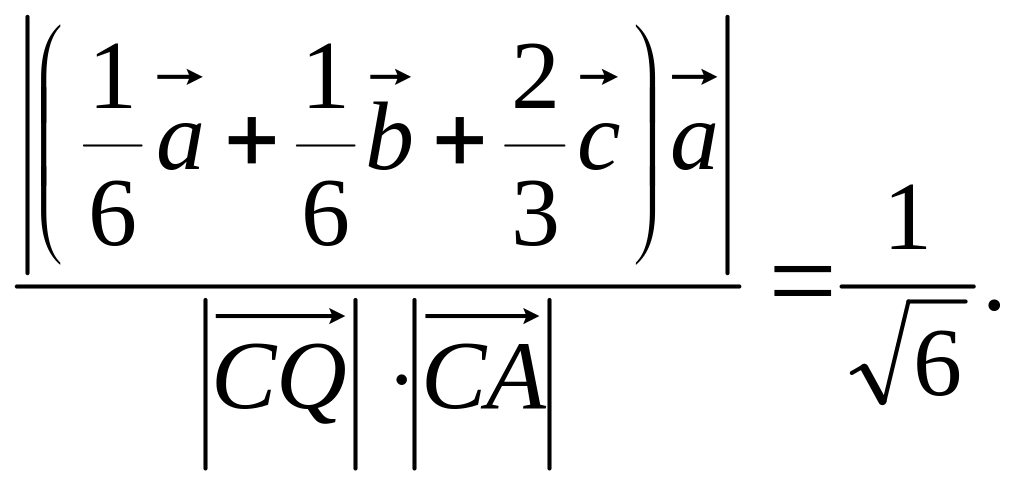
(ABD,CBD) = arccos

Ответ. а) 60°; б) arcsin ; в) arccos ; г) arccos

Векторно-координатный и координатный методы

Косинус угла между ненулевыми векторами можно вычислить, зная координаты векторов: косинус угла между ненулевыми векторами и выражается формулой cos (5)

Тогда при нахождении углов в пространстве можно действовать по следующему плану:

1. ввести прямоугольную систему координат;

2. выбрать нужную из формул (1)-(4);

3. найти координаты векторов, входящих в формулу;

4. подставить найденные координаты в формулу, учитывая равенство (5), и произвести вычисления;

5. записать ответ.

При нахождении координат векторов, необходимых для решения, можно сначала получить векторные выражения, а затем перевести их на язык координат, а можно сразу использовать формулы метода координат. В первом случае говорят, что задача решена векторно-координатным, во втором – координатным методами. Проиллюстрируем эти методы на задаче 18.

Решение. Введем систему координат как показано на рисунке 31.

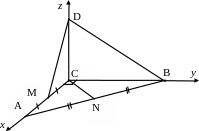
Рис. 31

Для решения нам потребуются координаты точек А, В, С, D. Исходя из условия, получим:

А (2;0;0), В (0;2;0), С (0;0;0;), D (0;0;1).

а) Используя формулы для вычисления координат середины отрезка по координатам его концов, находим:

М (1;0;0), N (1;1;0).

Тогда векторы и имеют координаты и

cos (DM,CN) = |cos ( )| = , или (DM,CN) = 60°.

б) Вектор имеет координаты а вектор , перпендикулярный плоскости ВСD, - координаты . Получим: sin (DN,BCD) = |cos ( )| = (DN,BCD) = arcsin

в) Плоскости АВС перпендикулярен вектор который имеет координаты

Координаты вектора , (Q АВD), перпендикулярного плоскости АВD, можно найти либо с помощью векторов, либо методом координат. Рассмотрим оба эти метода.

Векторно-координатный метод

Для нахождения координат точки Q воспользуемся результатами решения задачи 18,в векторным методом. Там мы нашли, что

где

Переходя от векторного равенства к координатам, и учитывая, что вектор имеет координаты получим:

т.е. вектор имеет координаты

Используя формулы (4) и (5), находим:

сos (АВD,АВС) = |cos | =

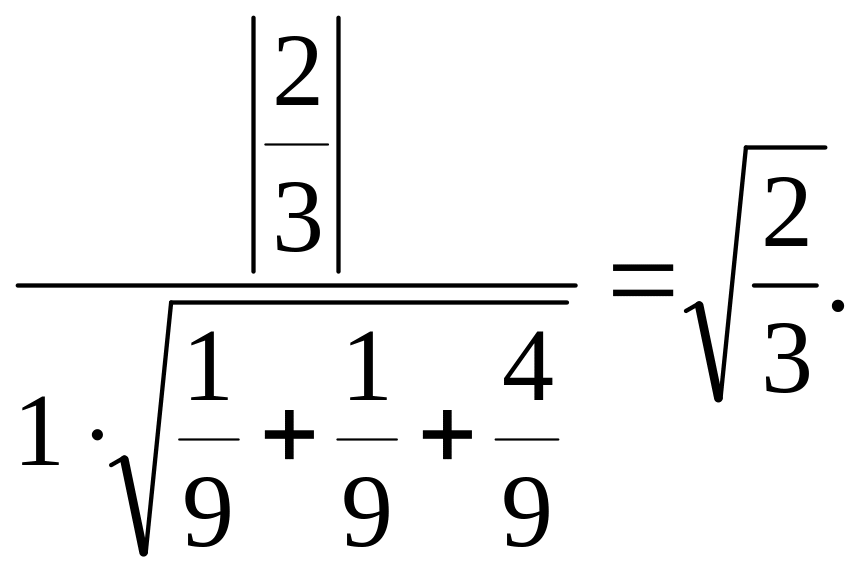
(АВD,АВС) = arccos .

Координатный метод

Используя уравнение плоскости в отрезках запишем уравнение плоскости АВD:

Из него находим, что вектор с координатами {1;1;2} перпендикулярен плоскости АВD.

Тогда получим:

сos (АВС,АВD) = (АВС,АВD) = arccos .

г) сos (АВD,СВD) = |сos | =

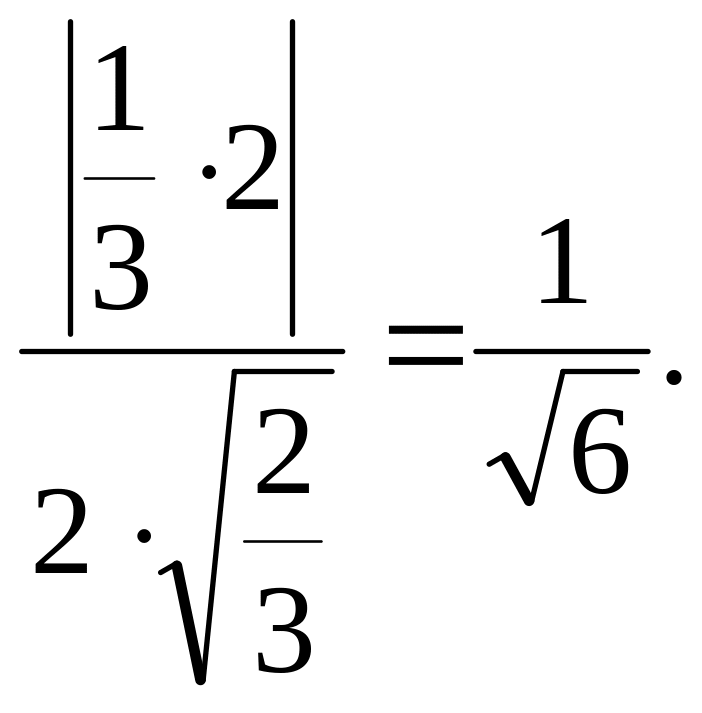
(АВD,СВD) = arccos

Ответ. а) 60°; б) arcsin ; в) arccos ; г) arccos

Сравнивая разные методы решения задачи 18, можно заметить, что для требований «а» и «б» все методы равноценны, может быть несколько сложнее конструктивный, поскольку он связан с дополнительными построениями. Для требования «в» конструктивный метод наиболее рационален. Самoе короткое решение задачи «г» дает метод координат, если введено уравнение плоскости в отрезках; конструктивный, векторный и векторно-координатный методы для требования «г», на наш взгляд, равноценны.

В заключение еще раз подчеркнем: при решении задач на нахождение углов необязательно знать длины отрезков, достаточно знать соотношение длин. Например, данные задачи 18 могли быть такими: Дан равнобедренный треугольник АВС с прямым углом С. Через вершину С проведена прямая CD, перпендикулярная плоскости АВС. На ней отложен отрезок CD, в два раза меньший катета АС. Далее по тексту задачи 18.

В таких случаях при решении вводится вспомогательный линейный элемент. Например, пусть длина отрезка CD равна а, тогда СА = СВ = 2а, АВ = 2а и т.д. В итоге это а сократится, исчезнет. Или можно меньший отрезок CD принять за единицу измерения, тогда СА = СВ = 2, АВ = и т.д.

Итак, для вычисления расстояний и углов мы рассмотрели основные методы – конструктивный и аналитические: векторный, векторно-координатный, координатный.

Какой метод выбрать при решении каждой конкретной задачи, предсказать довольно сложно. Одна из рекомендаций может быть такой: если условиями задачи определен прямой трехгранный угол (угол, у которого все плоские углы прямые), то можно пытаться использовать либо метод координат, либо конструктивный метод; если определен непрямой трехгранный угол, то более целесообразен векторный метод или конструктивный. Однако многое зависит и от того, что требуется найти.