5.4.Порядок расчета тока в ветви методом эквивалентного генератора

В заданной схеме требуется найти ток в одной ее ветви. Н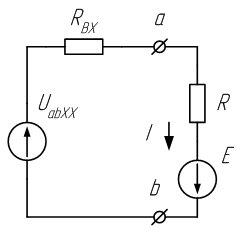 еобходимо выделить ветвь, в которой течет искомый ток, а остальную схему представить в виде активного двухполюсника. По отношению к выделенной ветви двухполюсник можно заменить эквивалентным генератором. ЭДС эквивалентоного генератора равна напряжению холостого хода на зажимах, а его внутреннее сопротивление равно Рисунок. 6 входному сопротивлению двухполюсника. Порядок расчета:

• заключить всю схему в прямоугольник, выделив из нее одну ветвь ab, в которой требуется найти ток I (рис.6). Ток в искомой ветви:

( 8)

где Uabxx - напряжение холостого хода, равное эквивалентной ЭДС двухполюсника, R_BX - входное сопротивление двухполюсника относительно зажимов ab, Е и R- соответственно ЭДС и сопротивление выделенной ветви;

- для нахождения U_abxx разомкнутой ветви воспользоваться любым из ранее рассмотренных методов расчета;

- определить входное сопротивление R_BX по отношению к зажимам ab при закороченных источниках ЭДС (т.к. R_вн идеального источника равно 0) и разомкнутых источниках тока (т.к. R_вн идеального источника тока равно ∞);

• определить ток в ветви I по формуле (8)

Перед ЭДС в (8) знак "+" ставится в том случае, если ее направление совпадает с направлением тока в ветви и "–" если оно противоположно.

5.5.Составление энергетического баланса в электрической схеме

Баланс в электрической схеме составляется на основе закона сохранения энергии. При составлении энергетического баланса необходимо:

- рассчитать выделенную источниками энергию в единицу времени по формуле:

(9)

где первое слагаемое представляет собой мощность источников ЭДС, а второе – мощность источников тока. Если направление тока I, протекающего через источник ЭДС Е совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь в единицу времени энергию, равную произведению Е·I и входит с положительным знаком в уравнение энергетического баланса. Если направление тока I не совпадает с направлением ЭДС, то перед произведением E·I ставим знак "–". Энергия, доставленная источниками тока J рассчитывается как произведение J·U_ав , где U_ав – напряжение на источнике тока. Считается, что к узлу (а) ток J_k источника тока подтекает, а от узла (в) он оттекает.

- рассчитать выделившуюся на сопротивлениях мощность по формуле:

(10)

- проверить уравнение энергетического баланса, приравняв выделяемую и потребляемую мощность Р₁=Р₂

Энергетический баланс в цепи синусоидального тока составляется также на основании закона сохранения энергии и говорит о том, что выработанная мощность равна потребляемой.

, (11)

где U -— комплексная разность потенциалов на зажимах источников, I* — сопряженный комплекс тока, протекающего через источник .

Активная мощность Р есть действительная часть (Re), a реактивная мощность Q — мнимая часть (Im) мощности источника. Потребленная мощность S выражается как , где I - действующее значение тока.

3.6. Показания приборов.

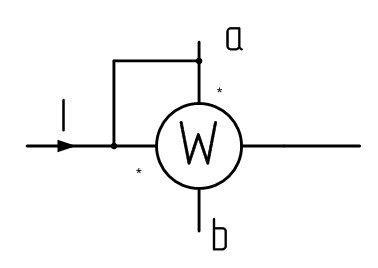
Рисунок 7

Ваттметр, изображенный на рис.7, измеряет активную мощность участка цепи, на котором он включен. Он содержит две катушки: подвижную и неподвижную. Подвижная катушка выполняется из тонкого провода. Ее 'включают параллельно участку цепи подобно вольтметру. Неподвижная катушка, выполненная из толстого провода, имеет малое сопротивление. Она включается в цепь последовательно. На концах одноименных зажимов (их соединяют) принято ставить звездочки или точки. Вращающий момент ваттметра, а следовательно, и его показания пропорциональны скалярному произведению напряжения Uаb параллельной обмотки на ток I, протекающий по последовательной обмотке. Напряжение на параллельной обмотке берется равным разности потенциалов между концом ее, обозначенным звездочкой, и концом, не обозначенным звездочкой. Ток I входит в конец последовательной обмотки, обозначенной звездочкой. Р = U_abI cos(U_ab^I). Если известны комплексы тока I и напряжения иU_ab, то показания вольтметра можно определить как Р =Re[U_ab·I*] , где I* — сопряженный комплекс тока равный I* = Ie^-jφ, если прямой комплекс тока I = Ie^-jφ .

3.7. Векторная диаграмма токов и топографическая диаграмма

Для построения векторной диаграммы токов необходимо все токи схемы представить на комплексной плоскости как показано на рисунке 8.

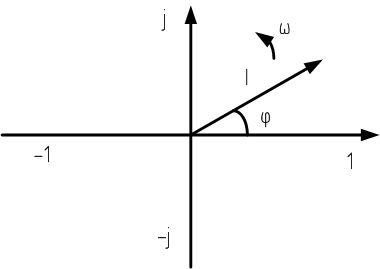
Рисунок 8

Длина вектора I соответствует модулю комплексной величины, а угол φ откладывается от оси действительных чисел в сторону вращения вектора, то есть против часовой стрелки (рис. 8). После изображения всех токов необходимо проверить графически выполнение первого закона Кирхгофа на комплексной плоскости.

Построим топографическую диаграмму для схемы, изображенной на рис.9 . Направим вектор тока I, как показано на рисунке. Примем потенциал точки g равным нулю (φ_g=0). Определим потенциалы остальных точек.

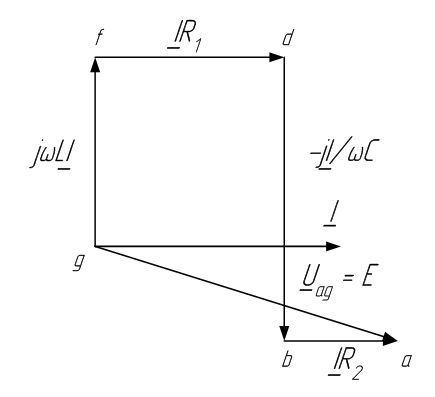
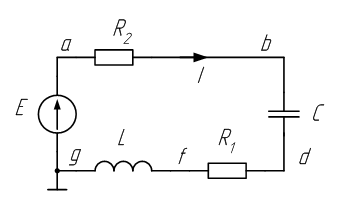
Рисунок 9

Будем обходить схему, начиная от точки g навстречу положительному направлению тока. Потенциал точки f больше потенциала точки g на величину падения напряжения на катушке индуктивности, φ_f=φ_g+jωLI. Конец его обозначим буквой f т.к. он определяет потенциал этой точки . Потенциал точки d выше потенциала точки f на величину падения напряжения на сопротивлении R: φ_d=φ_f+R_1*I. Отложим от конца вектора gf вектор IR₁, параллельный току. Конец вектора IR₁ обозначим буквой d Аналогично находим φ_b=φ_d – (j/ωC)I, и потенциал точки а: φa=φb+IR₂, (рис. 9).

3.8. Расчет разветвленных цепей при наличии взаимной индуктивности

Расчет разветвленных цепей можно выполнить, составляя уравнения по первому и второму законам Кирхгофа. При составлении уравнения по второму закону Кирхгофа ЭДС взаимной индукции обычно учитываются как соответствующие напряжения на индуктивности. Знак магнитного комплексного напряжения на элементе k определяется на основании сопоставления направления обхода контура через элемент k и положительного направления тока в элементе s. Если эти направления относительно одноименных выводов одинаковы, то составляющая напряжения jωM_ksI_s берется со знаком (+). В противном случае – со знаком (–). Найти величину М можно, используя соотношение , где L_{1 ,}L₂ – индуктивности катушек, M– взаимная индуктивность.

4. ПОРЯорядок защиты и ответственность студента за выполнение расчетно-графических работ работы

В процессе подготовки к выполнению расчетно-графической работы (РГР) студентами изучаются разделы "Цепи постоянного тока", "Методы расчета цепей постоянного тока" по указанной литературе. Приступая к выполнению работы, студенты должны:

- изучить и уметь применять на практике методы расчета цепей постоянного тока произвольной конфигурации с источниками ЭДС и тока;

• оценивать полученные результаты;

• владеть методами расчета цепей постоянного тока на ЭВМ;

Знания и навыки, приобретенные студентами в процессе изучения метода анализа электрических цепей постоянного тока, необходимы для успешного усвоения последующих разделов курса "Основы теории цепей" и "Теоретические основы электротехники", а также других электрических дисциплин, предусмотренных программой подготовки инженеров электрических специальностей. Исправление ошибок следует делать на обратной стороне листа или чистом листе. Не допускается стирать ошибки и листы заменять новыми.