4. Общие требования к написанию расчетно–графической работы

4.1. Оформление РГР: РГР выполняется на листах стандартных размеров формата А 4, заполненных с одной стороны. Листы нумеруются и оставляются поля: слева для подшивки 25-30 мм, справа-10 мм, снизу и сверху-20 мм. При оформлении отчета строго соблюдаются ГОСТ и ЕСКД. Титульный лист оформляется по прилагаемому образцу (см. приложение 2) и выполняется тушью, черной пастой или отпечатывается на плотной бумаге.

Первые листы содержат текст задания, схемы и исходные данные расчетного варианта. Расчеты и необходимые пояснения выполняются на остальных листах отчета. В конце текста прилагаются необходимые распечатки, отражающие машинный расчет электрических схем.

Структура РГР должна соответствовать пунктам задания. Отдельные части должны иметь заголовки, комментарии и выводы. Записи и формулировки должны быть точными и ясными. При численных значениях должны быть обязательно указаны единицы измерения. Графики и диаграммы рекомендуется делать в масштабе на миллиметровой бумаге. По осям координат должны быть указаны единицы измерения. В конце должен быть приведен список использованных источников.

5. Рекомендации по организации выполнения расчетно-графических работ, примерный календарный план выполнения

Задание на РГР выдается преподавателем каждому студенту индивидуально. При этом указывается вариант задания. Предлагаемые к решению задачи в РГР должны рассматриваться и решаться студентами по мере прочтения лекционного материала и представляться для обсуждения и проверки преподавателю. Успешное выполнение РГР во многом зависит от систематического и планомерного выполнения студентом графика календарного плана его выполнения (см. таблицу 4). При необходимости после представления РГР защищается студентом.

Таблица 4 – Сроки представления материалов РГР

Разделы задания	Наименование раздела в задании	Объем в %	Срок представления
1	Расчет линейных цепей постоянного тока	50	Через 4 недели после выдачи задания
2	Расчет линейных цепей переменного тока	50	Через 8 недель после выдачи задания

5.1. Последовательность расчета токов в цепи законами Кирхгофа

-Выбрать произвольные положительные направления токов ветвей и обозначить их на схеме.

-Составить (у-1) уравнений по первому закону Кирхгофа, где у - число узлов схемы. Следует учесть и токи источников тока.

( 1 )

если ток подходит к узлу, то его значение берется со знаком "+" если отходит от узла – со знаком "–".

-Выбрать произвольные направления обхода независимых контуров. Составить (в-в_ит)-(у-1) уравнений по второму закону Кирхгофа для независимых контуров (в- число ветвей , в_ит -число ветвей, содержащих источники тока).

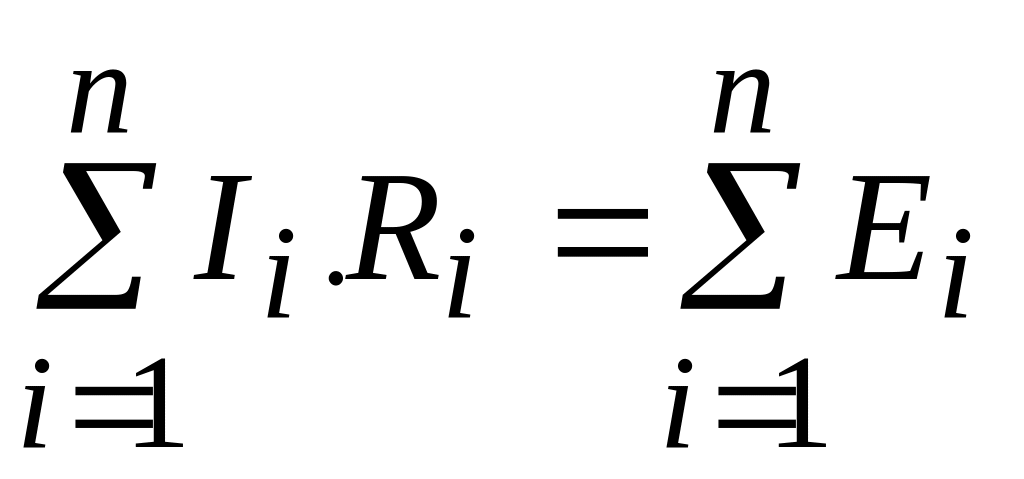( 2 )

-Объединить и совместно решить систему уравнений (1) и (2), находя токи в ветвях схемы. Если в результате решения этих уравнений получится отрицательное значение какого-либо тока, то действительное его направление противоположно принятому за положительное.

При составлении уравнений законами Кирхгофа для цепей синусоидального тока необходимо помнить о том, что законы Кирхгофа справедливы для мгновенных величин или для комплексов : а) (3)

б) , (4)

где соотношения между мгновенными напряжениями на индуктивности, емкости и активном сопротивлении:

u_L = L∙di/dt, u_c = l/C∙∫idt, u_r= i∙R,

.Для написания уравнений в комплексной или символьной форме записи необходимо в системе уравнений (3–4) провести следующие замены: i→I_m,, u_R→ImּR, u_L→iωLּI_m,, e→E_m, u_c →-(i/ωc)ּI_m.

После перехода к символической форме решить совместно уравнения, записанные по первому и второму законам Кирхгофа.

5.2. Последовательность расчетов токов методом узловых потенциалов

• обозначить узлы в схеме, потенциал одного из узлов принять равным 0.

• для оставшихся Y-1 узлов записать следующую систему уравнений:

G_11∙φ₁ –G_12∙ φ₂ –G_13∙ φ₃–…– G_{1 (y-1)} = J11

–G_21∙φ₁+G_22∙ φ₂–G_23∙ φ₃–…– G_{2 (y-1)} =J₂₂ (5)

…………………………………………….

–G_(y-1)1∙φ₁–G_(y-1)2∙ φ₂–G_(y-1)3∙ φ₃–…+ G_(y-1)1(y-1) = J_(y-1)1(y-1)

где Gpp с двумя одинаковыми индексами представляет собой суммарную проводимость ветвей, присоединенных к узлу р и называется собственной узловой проводимостью, проводимость G_ip = G_pj с двумя различными индексами равна сумме проводимости ветвей, соединяющих между собой рассматриваемые узлы i и р, и называется общей узловой проводимостью этих узлов. = (6)

где J_ii, узловой ток, состоящий из J_i,– токов источников тока, присоединенных к i-му узлу и токов EiּGj ветвей с источниками ЭДС, присоединенных к узлу.

Алгебраическое суммирование выполняется с учетом знаков. Знак "+" ставится в том случае, если ток источника тока и ЭДС источника ЭДС направлены к узлу. Если в схеме имеется ветвь с идеальным источником ЭДС, то разность потенциалов между зажимами источника ЭДС известна и равна ЭДС. Если принять один из потенциалов равным 0, второй определяется как φ = ±Е, и число уравнений сократится до (Y–2);

• решить систему (5–6) уравнений относительно потенциалов узлов схемы.

• рассчитать токи в ветвях, пользуясь законом Ома для участка цепи.

( 7 )

где φ_i– потенциал узла, от которого течет ток I_i, φ_к – потенциал узла, к которому подтекает I_i, Е_i - величина источника ЭДС i–й ветви (берется со знаком "+", если направление ЭДС Е_i совпадает с током I_i и "–" если оно противоположно) R_i - сопротивление i-й ветви. Для цепи синусоидального тока:

- заменить мгновенные значения ЭДС и токов на комплексные, ввести комплексную проводимость Y=g ± jb , где g – активная часть, b - реактивная часть проводимости;

- для каждого из (у -1) узлов составить уравнения: Y₁₁·φ₁ – Y₁₂ ·φ₂– ….– Y_{1. y-1 ·}φ_{1. y-1}= I₁

Y₂₁φ₁ – Y₂₂φ₂– ….– Y_{1. y-2}φ_{1. y-1}= I₂ (8)

………………………………………………. Y_{(y-1)1 ·}φ₁ – Y_{(y-1)2 ·}φ₂- ….- Y_{. (y-1) (y-1)··} φ_{(y-1) (y-1)}=I_(y-1)

где φ_i – потенциал соответствующего узла, y_ii – комплексная проводимость i – го узла, Yji – сумма проводимостей ветвей, соединяющих узлы i и j. Далее решение системы производится аналогично цепи постоянного тока.

3.3 Последовательность расчета токов в цепи методом контурных токов

При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Число уравнений, которые необходимо составить в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа, то есть n=b-b_ит Последовательность расчета:

- выбрать взаимно независимые контуры;

- выбрать направления контурных токов (желательно для всех токов

одинаковые);

- записать следующую систему уравнений для n контуров:

I_11*R₁₁ + I_{22 ∙}R₁₂ + I_33∙R₁₃+…+ I_nn∙R_1n=E₁₁

I_11*R₂₁₊I_{22 ∙}R_22- I_{33 ∙}R₂₃ +…+ I_nn ∙R_2n=E₂₂ (9)

I_11*R₃₁ +I_{22 ∙}R₃₂ + I₃₃ ∙R₃₃+…+ I_nn ∙R_3n=E₃₃

_{………………………………………………………………………….}

I_11*R_n1 +I_{22 ∙}R_n2 + I_{33 ∙}R_n3+…+ I_{nn ∙}R_nn=E_nn

где R_ii, - собственные сопротивления контуров, равные сумме сопротивлений, входящих в i-й контур, R_ji – сопротивления смежных ветвей между j и i контурами. Е_ii- контурная ЭДС 1-го контура, равная алгебраической сумме ЭДС, входящих в i-й контур. В нее со знаком "+" входят те ЭДС, направление которых совпадает с направлением контурных токов. Если направления контурных токов выбраны одинаково, то сопротивления смежных ветвей R_ij входят в (9) со знаком "–", так как направления контурных токов I_ii и I_jj в этой ветви противоположны. Если направления токов в смежных ветвях одинаковы, то сопротивление r_ij входит в систему (9) со знаком "+".

• р ешить систему (9) относительно контурных токов, затем рассчитать токи в ветвях как I_i = I_ii для ветвей, по которым протекает один контурный ток и Ii = ±I_ii ±I_jj для токов в ветвях, где встречаются два контурных тока, причем слагаемое берется со знаком "+", если направление тока в ветви и контурного тока совпадают, и со знаком "–" – если они противоположны. Составлению уравнений по методу контурных токов для схем с источниками тока присущи некоторые особенности. Ток каждого из источников тока полагают входящим в контур, замыкающийся по любым ветвям схемы. Падение напряжения, вызываемое током такого источника на каждом из сопротивлений контура, учитывается при

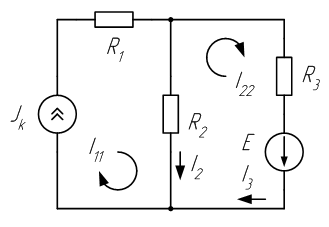
записи левой части уравнений. Уравнения составляются лишь для

Рисунок 5 контуров с неизвестными токами. Например, для схемы, изображенной на рисунке 5 контурный ток I₁₁= J_k течет согласно направлению обхода по часовой стрелки по ветвям 1 и 2; то по методу контурных токов необходимо составить только одно уравнение:

, отсюда .

Ток I₂ = J_k – I_{22 ,} I₃ = I₂₂

Для цепи синусоидального тока:

- заменить мгновенные значения ЭДС, токов на комплексные, ввести комплексные сопротивления Z = R ± jX с действительной частью R и мнимой частью X. При наличии в схеме источника тока, либо преобразовать его в источник ЭДС, либо добавить к выбранным контурам еще один контур с ветвью, содержащей источник тока, контурный ток этого контура известен и равен току источника тока;

- для каждого независимого контура составить контурные уравнения:

Z_11·· I₁₁ + Z₁₂ ·I_22…+_.Z_1,n I_nn = E₁₁

Z_{21 ·}I₁₁ + Z₂₂ ·I_22+….+ Z_2,n· I_nn = E₂₂ (7)

…………………………………………………………. Z_{n1 ·} I₁₁ + Z_n2 I_22…+_.Z_1,n I_nn = E₁₁

где: I_ii- контурный ток i-ro контура.

Z_ii – собственное сопротивление i-того контура, равное сумме сопротивлений ветвей, входящих в этот контур, Z_ij - сопротивление ветви, входящей одновременно в i и j контуры, взятое со знаком плюс, если направления контурных токов I_ii и Ijj вдоль этой ветви совпадают, и со знаком минус – если они противоположны, E_ii – контурная ЭДС i-того контура, равная алгебраической сумме ЭДС, входящих в этот контур и взятых со знаком плюс, если направления этих ЭДС совпадают с направлением тока I j j;

- решить систему ( 7 ) и найти контурные токи аналогично постоянному току.