13. Векторы на плоскости и в пространстве

Вектором называется направленный отрезок AB с начальной точкой A и конечной точкой B (который можно перемещать параллельно самому себе).

 Длиной вектора AB называется число AB, равное длине отрезка AB, изображающего вектор.

Произведением вектора a на число  называется вектор b=a, имеющий длину b=a, направление которого совпадает с направлением вектора a, если >0, и противоположно ему, если <0.

Суммой двух векторов a и b называется вектор c=a+b, начало которого совпадает с началом вектора a, а конец - с концом вектора b при условии, что начало вектора b совпадает с концом вектора a. Вектор c в этом случае представляет собой диагональ параллелограмма, построенного на векторах a и b (правило параллелограмма).

Разностью двух векторов a и b называется сумма вектора a и вектора (-1)b.

 Векторы, лежащие на одной прямой (или на параллельных прямых) называются коллинеарными, векторы, лежащие в одной плоскости, называются компланарными.

Координатами вектора a называются координаты его конечной точки, если так переместить вектор параллельно самому себе, чтобы его начало совпало с началом координат.

На плоскости Oxy вектор имеет две координаты: a(x₁, y₁) и b(x₂, y₂).

В пространстве Oxyz вектор имеет три координаты: a(x₁, y₁, z₁) и b(x₂, y₂, z₂).

Линейные операции в координатной форме:

1) произведение вектора a=(x, y, z) на число , есть вектор b=( x,  y,  z);

2) суммой и разностью векторов a(x₁, y₁, z₁) и b(x₂, y₂, z₂) являются соответственно векторы c=a+b=(x₁+x₂, y₁+y₂, z₁+z₂) и d=a-b=(x₁-x₂, y₁-y₂, z₁-z₂);

Длина вектора a(x, y, z) вычисляется по формуле a =  .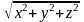

14. Скалярное произведение двух векторов (определение) и его выражение в координатной форме. Угол между векторами

Определение 1. Скалярным произведением (a, b) двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

(a, b) = abcos  .

В координатной форме скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.

Если a(x₁, y₁) и b(x₂, y₂), то (a, b) = x₁x₂ + y₁y₂ .

Если a(x₁, y₁, z₁) и b(x₂, y₂, z₂), то (a, b) = x₁x₂ + y₁y₂ + z₁z₂ .

Угол между векторами вычисляется по формуле .

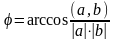15. n-мерный вектор. Линейная комбинация, линейная зависимость и независимость векторов

Определение 1. n-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде x = (x₁, x₂, …, x_n), где x_i есть i-ая компонента вектора x.

Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, то есть x = у, если x_i = y_i, для  = 1, 2, …, n.

Определение 2. Суммой двух векторов одинаковой размерности n называется вектор z = х + у, компоненты которого равны сумме соответствующих компонент слагаемых векторов, то есть z_i = x_i + y_i для  = 1, 2, … , n.

Определение 3. Произведением вектора x на действительное число  называется вектор u=x, компоненты u_i которого равны произведению  на соответствующие компоненты вектора x, то есть u_i = x_i  для  = 1, 2, … , n.

Определение 4. Вектор a_m называется линейной комбинацией векторов a₁, a₂, ..., a_m-1, если a_m = ₁ a₁+₂ a₂+ ... +_m-1 a_m-1, где ₁, ₂, ... , _m-1 – некоторые действительные числа.

Определение 5. Векторы a₁, a₂, ..., a_m называются линейно зависимыми, если существуют такие числа ₁, ₂, ... , _m , не равные нулю одновременно, что линейная комбинация ₁ a₁+₂ a₂+ ... +_m a_m равна нулевому вектору.

В противном случае векторы называются линейно независимыми.

16. Векторное (линейное) пространство, его размерность и базис.

Векторным (линейным) пространством называется множество n-мерных векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие определенным свойствам (аксиомам).

Линейное пространство называется n-мерным, если в нем существует n линейно независимых векторов, а любые из (n + 1) векторов являются линейно зависимыми

 Совокупность n линейно независимых векторов n-мерного пространства называется базисом.

Теорема 1. Каждый вектор линейного пространства можно представить и притом единственным образом в виде линейной комбинации векторов базиса

x = x₁ e₁+ x₂ e₂+ ... +x_n e_n.

Представление произвольного вектора линейного пространства в виде линейной комбинации векторов базиса этого пространства называется разложением данного вектора по базису.

17. Скалярное произведение векторов в n-мерном пространстве.

Скалярным произведением двух векторов x = (x₁, x₂, … x_n) и y = (y₁, y₂, … y_n) n-мерного пространства называется число

(x, y) = x₁y₁ + x₂y₂ + … + x_ny_n .

. Евклидовым пространством называется линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее определенным условиям (аксиомам).

 Длиной (нормой) вектора в евклидовом пространстве называется корень квадратный из его скалярного квадрата

.
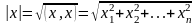