
- •30. Общее уравнение плоскости в пространстве и его частные случаи. Нормальный вектор плоскости. Условия параллельности и перпендикулярности двух плоскостей
- •32. Углы между двумя плоскостями, между двумя прямыми, между прямой и плоскостью. Условия параллельности и перпендикулярности двух плоскостей, двух прямых, прямой и плоскости
- •27. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых
- •Кривые второго порядка, их общее уравнение. Нормальное уравнение окружности. Каноническое уравнение эллипса. Геометрический смысл параметров окружности и эллипса
- •29. Канонические уравнения гиперболы и параболы, геометрический смысл их параметров. Уравнение асимптот гиперболы. График обратно пропорциональной зависимости и квадратного трехчлена
- •20. Матрица линейного оператора в заданном базисе: связь между вектором х и образом у.
- •21. Собственные векторы и собственные значения матрицы.
- •22. Матрица линейного оператора в базисе, состоящем из его собственных векторов
- •23. Квадратичная форма (определение). Матрица квадратичной формы. Ранг квадратичной формы
- •24. Квадратичная форма (канонический вид). Приведение квадратичной формы к каноническому виду. Закон инерции квадратичных форм
- •26. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести)
- •Билет1. Понятие матрицы.
- •Билет2. Определители 2-го и 3-го порядков.
- •Свойства определителей
- •Теорема Лапласа о разложении определителя по элементам строки или столбца
- •4. Понятие минора k-го порядка. Ранг матрицы (определение). Вычисление ранга матрицы с помощью элементарных преобразований
- •3. Особенная и неособенная квадратные матрицы.
- •5. Линейная независимость столбцов (строк) матрицы. Теорема о ранге матрицы
- •18. Ортогональные векторы. Ортогональный и ортонормированный базисы.
- •19. Определение оператора.
- •13. Векторы на плоскости и в пространстве
- •14. Скалярное произведение двух векторов (определение) и его выражение в координатной форме. Угол между векторами
- •16. Векторное (линейное) пространство, его размерность и базис.
- •17. Скалярное произведение векторов в n-мерном пространстве.
- •6. Система n линейных уравнений с n переменными (общий вид).
- •7. Решение системы n линейных уравнений с n переменными по формулам Крамера
- •8. Решение системы n линейных уравнений с n переменными
- •9. Метод Гаусса решения системы n линейных уравнений с n переменными. Понятие о методе Жордана-Гаусса
- •10. Система m линейных уравнений с n переменными. Теорема Кронекера-Капелли. Условия определенности и неопределенности совместной системы линейных уравнений
- •11. Базисные (основные) и свободные (неосновные) переменные системы m линейных уравнений с n переменными. Базисное решение
- •12. Система линейных однородных уравнений
3. Особенная и неособенная квадратные матрицы.
Квадратная матрица A называется особенной (вырожденной), если ее определитель равен нулю, т.е. A=0.
Квадратная матрица A называется неособенной (невырожденной), если ее определитель отличен от нуля, т.е. A0.
Матрица А-1 называется обратной по отношению к квадратной матрице n-го порядка A, если AА-1=А-1A=E, где E - единичная матрица n-го порядка.
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица А-1 существует (и единственна), тогда и только тогда, когда матрица A неособенная.
Необходимость. Пусть матрица A имеет А-1, т.е. АА-1=А-1A=Е. По свойству 10 определителей имеем АА-1=АА-1=Е=1, Следовательно, А0 и А-10
Достаточность. Пусть A0.
Рассмотрим
матрицу
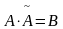 .
По правилу умножения матриц
.
По правилу умножения матриц
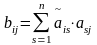 .
По определению присоединенной матрицы
и свойству 7 определителей
.
По определению присоединенной матрицы
и свойству 7 определителей
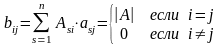 , т.е. В
- диагональная матрица, диагональные
элементы которой равны А.
, т.е. В
- диагональная матрица, диагональные
элементы которой равны А.
Аналогично
проверяется, что
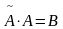 .
Итак, в качестве обратной матрицы можно
взять матрицу
.
Итак, в качестве обратной матрицы можно
взять матрицу
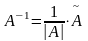 ,
так как
,
так как
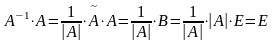 .
.
Единственность
обратной матрицы следует из того, что
если некоторая матрица Х
удовлетворяет условию обратной матрицы
АХ=Е,
то
 и
и
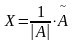 .
.
5. Линейная независимость столбцов (строк) матрицы. Теорема о ранге матрицы
Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов.
Пусть
дана матрица
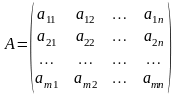 .
Для ее строк введем обозначения: e1=(a11,
a12,
... , a1n),
e2=(a21,
a22,
... , a2n),
..., em=(am1,
am2,
... , amn)
.
.
Для ее строк введем обозначения: e1=(a11,
a12,
... , a1n),
e2=(a21,
a22,
... , a2n),
..., em=(am1,
am2,
... , amn)
.
Две строки матрицы называются равными, если равны их соответствующие элементы.
Операции умножения строки на число и сложения строк вводятся как операции проводимые поэлементно.
Строка е называется линейной комбинацией строк e1, e2, ... , es, матрицы, если е=1e1+2 e2+ ... +s es, где 1, 2, ... , s - произвольные числа.
Строки матрицы e1, e2, ... , es называются линейно зависимыми, если существуют такие числа 1, 2, ... , s не равные нулю одновременно, что линейная комбинация 1e1+2 e2+ ... +s es равна нулевой строке.
Линейная зависимость всех строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных строк.
Строки матрицы e1, e2, ... , es называются линейно независимыми, если их линейная комбинация 1e1+2 e2+ ... +s es равна нулевой строке тогда и только тогда, когда все коэффициенты 1, 2, ... , s равны нулю.
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки (столбцы).
