3.Описание входного сигнала.

1. 3.1. Импульсный сигнал.

Сигнал называется импульсным, если он отличен от нуля на конечном интервале времени. На вход линии подается простейший импульсный сигнал- одиночный прямоугольный импульс (рис. 3). Аналитически он описывается так

, (6)

где -единичная функция, для ее описания использована функция единичного включения (функция Хевисайда) : .

Спектральная плотность этого сигнала определяется по формуле

. (7)

Интеграл может быть вычислен и поэтому спектральная плотность считается заданной в аналитическом виде.

3.2. Периодический сигнал.

Другим типом входного сигнала является периодическая последовательность одиночных прямоугольных импульсов, описанных в предыдущем пункте. Периодический сигнал (см.Л.4, Рис.7) может быть представлен следующим образом . Его спектральное представление (дискретный комплексный спектр) есть последовательность спектральных компонент . Они являются коэффициентами ряда Фурье для периодического сигнала

, (8)

Вычисляются спектральные компоненты ряда (8) по известным формулам

. (9)

Так как сигнал представлен четной функцией времени, спектральные компоненты вещественны. Спектральные компоненты могут быть вычислены при известной спектральной плотности и поэтому считаются известными в аналитическом виде.

4.Полосковая линия как четырехполюсник.

Любая длинная линия представляет собой четырехполюсник: к входной паре полюсов подключается источник напряжения (в общем случае, может подключаться любой активный двухполюсник), а к выходной паре полюсов подключена нагрузка.

Предполагая, что входной сигнал гармонический, для четырехполюсника вводят понятие коэффициента передачи по напряжению 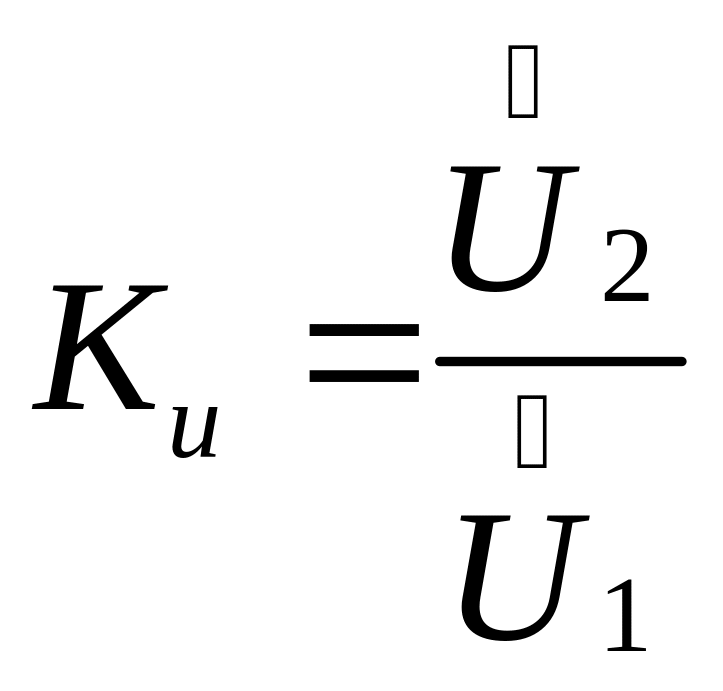как отношение комплексной амплитуды на выходе к комплексной амплитуде на входе. В случае согласованной нагрузки коэффициент передачи называется характеристическим передаточным коэффициентом Для любого четырехполюсника он равен , где -характеристический коэффициент передачи. В частном случае согласованной по нагрузке длинной линии комплексная амплитуда на выходе следующим образом зависит от комплексной амплитуды на входе : , где l-длина линии, а -ее коэффициент распространения. Следовательно, для согласованной длинной линии характеристический передаточный коэффициент равен . Как функция частоты он носит название передаточной функции длинной линии: . Коэффициенты ослабления и фазы могут быть рассчитаны только численно с использованием ПК, поэтому и передаточная функция должна быть включена в общий алгоритм вычислений.

5. Описание выходного сигнала.

1. Реакция на импульсный входной сигнал.

Выходной сигнал любого четырехполюсника определяется как непрерывная суперпозиция гармоник c помощью прямого преобразования Фурье.

. (10)

Амплитуды гармоник определяются спектральной плотностью выходного сигнала. Эта плотность естественным образом представляет собой спектральную плотность входного сигнала, умноженную на передаточный коэффициент четырехполюсника: .

Наибольший интерес представляет не реальный выходной сигнал, а его отклонение от идеального (ожидаемого) выходного сигнала, т.е. от сигнала . Это отклонение позволяет оценить качество передачи через длинную линию. Величина отклонения определяется по формуле

, (11)

где

, . (12)

В формулах (11) и ( 12) учтено, что в реальной линии .Это условие называется отсутствием фазовой дисперсии (фазовая скорость не зависит от частоты) .

Аналитический расчет целесообразно провести и во временной области с использованием преобразования Лапласа. Передаточная характеристика цепи имеет вид , при малых значениях характеристику можно представить в виде

, тогда (13)

а изображение выходного сигнала (14)

При расчетах сравнить результаты, полученные с помощью преобразования Фурье (10) и Лапласа(14).