Свойства математического ожидания

1. Математическое ожидание постоянной величины равно самой постоянной:

2. Постоянный множитель можно выносить за знак математического ожидания

3. Для постоянной величины имеем : при сдвиге всех значений с.в. на одно и то же число происходит соответствующий сдвиг в значении математического ожидания.

4. Обобщение свойств 2 и 3: Если и константы, то

5. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих случайных величин:

6. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий этих случайных величин:

7. Пусть случайная величина является функцией от случайной величины : . Тогда математическое ожидание случайной величины Y равняется:

Дисперсия дискретной с.В.

Можно достаточно легко указать такие случайные величины, которые имеют одинаковые математические ожидания, но различные возможные значения. По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Для оценки величины рассеивания значений с.в. вокруг ее математического ожидания вводят понятие дисперсии.

Отклонением называют разность между случайной величиной и ее математическим ожиданием . Отклонение имеет важное свойство: Математическое ожидание отклонения всегда равно нулю: . По этой причине отклонение мало подходит для оценки величины рассеивания значений с.в. вокруг среднего значения. Дисперсией (рассеиванием) дискретной с.в. называют математическое ожидание квадрата отклонения с.в. от ее математического ожидания.

Поскольку математическое ожидание и дисперсия имеют различные единицы измерения, наряду с дисперсией рассматривают функцию среднеквадратичного отклонения. Средним квадратичным отклонением с.в. Х называется квадратный корень из дисперсии:

Пример 1.24: Найти дисперсию для случайной величины, описанной в примере 4.4.

Решение. Поскольку математическое ожидание равно 1,5(см. пример 1.23), то используя таблицу описания случайной величины, имеем

Свойства дисперсии

1. Чем меньше дисперсия, тем более тесно группируются результаты конкретных испытаний относительно математического ожидания.

2. Если дисперсия равна 0, то X - const.

3. Для любой константы выполняется и

4. 

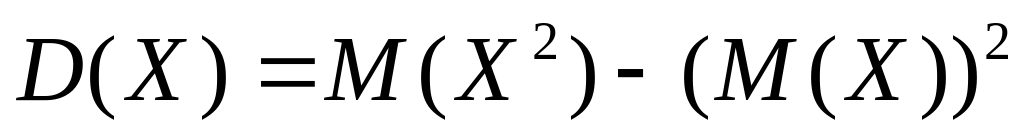
5. Дисперсия суммы конечного числа взаимно независимых с.в. равно сумме дисперсий этих величин

Другое решение задачи 1.24. Поскольку математическое ожидание равно 1,5(см. пример 1.23), а математическое ожидание квадрата случайной величины равно , то

Закон больших чисел.

Рассмотрим независимые одинаково распределенные случайные величины X₁, X₂, ..., X_n с конечными математическим ожиданием и дисперсией . Обозначим через среднее арифметическое этих с.в. Тогда для любого имеет место соотношение .

Этот результат называется законом больших чисел и утверждает, что для большого числа независимых случайных величин отклонение среднего арифметического их значений от математического ожидания будет по абсолютной величине сколь угодно малой:

.

Другими словами, при числе испытаний, стремящихся к , среднее арифметическое независимых случайных величин по вероятности (почти всегда, с вероятностью 1) сходится к математическому ожиданию.

Благодаря закону больших чисел мы можем рассматривать вероятность события как предельное значение частоты при достаточно большом числе испытаний. Как уже упоминалось, французским естествоиспытателем А.Бюффоном был проведен эксперимент: он подбросил монету 4040 раз, при этом орел выпал 2048 раз, а решка 1992 раза. Отсюда, частота выпадения орла составила 2048/4040 = 0,507 и отклонилась от вероятности его выпадения в каждом отдельном случае, равной 1/2, лишь на 0,007. Это говорит о том, что в рассматриваемом опыте почти полностью проявилось влияние основных, постоянных причин, а случайные причины отклонили результаты только на весьма незначительную величину. Т.е. в результате взаимопогашения случайных отклонений средние, исчисленные для величин одного и того же вида, становятся типичными, отражающими действие постоянных и существенных факторов в данных условиях времени и места.