4. Контрольные вопросы

1. Что такое поле? Назовите характеристики поля.

2. Дайте определение вектора магнитной индукции магнитного поля. Укажите единицы измерения индукции магнитного поля.

3. Изобразите силовые линии магнитного поля соленоида.

4. Сформулируйте закон Био-Савара-Лапласа. Расскажите о его применении.

5. Расскажите о силе Ампера и силе Лоренца.

6. Запишите формулу для расчета магнитного поля на оси соленоида конечной длины и бесконечно длинного соленоида.

7. Объясните характер распределения магнитного поля вдоль оси соленоида, полученный в работе.

Лабораторная работа № 9 изучение затухающих колебаний в контуре

Цель работы: изучение процессов в колебательном контуре, имеющем электроемкость, индуктивность и сопротивление; определение периода, частоты и логарифмического декремента колебаний.

Приборы и материалы: лабораторный стенд, имеющий набор объектов на плате; генератор сигналов; осциллограф; набор соединительных проводов.

1. Краткая теория

Причиной возникновения колебаний чаще всего является вывод (отклонение) системы из положения равновесия и предоставление ее самой себе. Тогда она начинает совершать колебания около положения равновесия. Такие колебания называются собственными (свободными) колебаниями системы.

Вследствие неизбежных потерь энергии колебательного движения (трения в механических системах, нагревания проводника, диэлектрика в конденсаторе, излучение электромагнитных волн в электрических колебательных системах и т.п.), колебания в системе постепенно затухают, и она возвращается в исходное состояние. Поэтому собственные колебания всегда являются затухающими.

З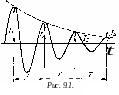 атухающие колебания не являются периодическими. Условным периодом (чаще говорят просто – периодом) затухающих колебаний называется промежуток времени между двумя последовательными максимальными или минимальными значениями колеблющейся величины. На рис. 9.1 представлены затухающие колебания электрического тока и указаны условные периоды затухания.

По своей природе колебания могут быть механическими, электромагнитными, электромеханическими и т.п. Электрические колебания могут возникать в цепи, содержащей индуктивность и емкость. Такую цепь называют колебательным контуром.

Понять процессы, происходящие в колебательном контуре, поможет рис. 9.2.

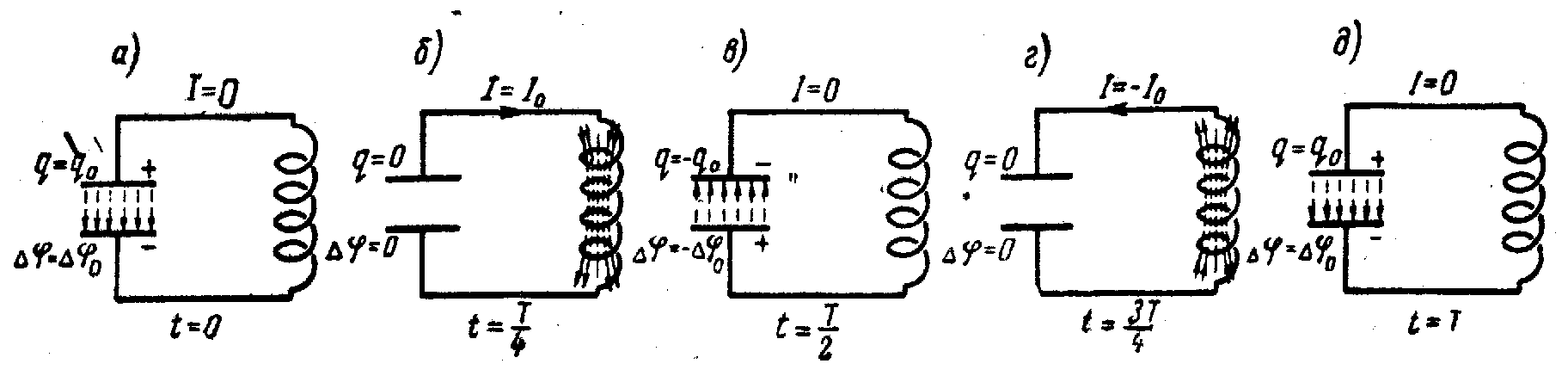
Рис. 9.2.

На рис. 9.3 изображен колебательный контур с параллельным соединением индуктивности и емкости . Сопротивлением здесь учитывается тот факт, что во всяком реальном контуре есть потери энергии и, простоты ради, будем полагать, что они происходят только в этом сопротивлении. Возбуждение колебаний в данном контуре производится путем подачи на него коротких импульсов напряжения, равных по длительности времени обратного хода луча осциллографа.

З а время длительности импульса конденсатор заряжается до напряжения . При разряде конденсатора через и в катушке возникает ЭДС самоиндукции . В паузах между импульсами внешнее напряжение к контуру не приложено и по второму правилу Кирхгофа сумма падений напряжений на , , должна быть равна нулю:

(9.1)

Учитывая, что , и поделив обе части уравнения на , получаем дифференциальное уравнение затухающих колебаний:

. (9.2)

Решение уравнения (9.2) при < имеет вид:

, (9.3)

где – заряд на конденсаторе в момент времени , – коэффициент затухания, – циклическая частота затухающих колебаний.

. (9.4)

При малых затуханиях, т.е. при << :

. (9.5)

В соответствии с (9.3) напряжение на конденсаторе будет изменяться по закону:

. (9.6)

Энергия , запасенная в контуре за время длительности импульса, убывает по экспоненциальному закону:

.

Затухание колебаний при этом принято характеризовать логарифмическим декрементом колебаний , равным логарифму отношения амплитуд двух последовательных колебаний (рис. 9.4):

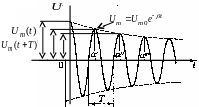
Рис. 9.4.

. (9.7)