Лабораторная работа № 8
Изучение магнитного поля соленоида
Цель работы: экспериментальное изучение распределения магнитного поля вдоль оси соленоида конечной длины.
Приборы и материалы: лабораторный стенд, имеющий соленоид, датчик индукционный на рейтере, плату объектов; генератор сигналов; осциллограф; прибор для изменения силы тока; набор соединительных проводов.
1. Краткая теория
Соленоидом называют катушку цилиндрической или иной формы из проволоки, витки которой намотаны в одном направлении (рис. 8.1).
М
Рис. 8.1.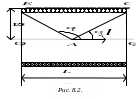
тично показано на рис. 8.2.
Распределение магнитной индукции по длине соленоида вдоль его оси О1О2 описывается выражением:
,
(8.1)
где
–
сила тока, протекающего по соленоиду;
– магнитная постоянная;
– число витков на единице длины;
и
– углы между осью соленоида (по направлению
вектора
)
и прямыми от исследуемой точки А до
концов соленоида (точки Е и С
соответственно).
Для бесконечно длинного соленоида
магнитная индукция
вычисляется по формуле:
. (8.2)
Индукция магнитного поля
в любой точке на оси соленоида конечной
длины всегда меньше индукции магнитного
поля бесконечно длинного соленоида в
раз, или с учетом (8.1) и (8.2):
,
откуда
.
(8.3)
Зная геометрические параметры соленоида
(длину
и диаметр
),
можно рассчитать
и
,
а следовательно, и индукцию магнитного
поля
для любой точки оси соленоида. Для центра
соленоида выражение для индукции
имеет наиболее простой вид (в этом случае
).
Обозначив
,
а
и подставив в (8.3) получим выражение для
индукции магнитного поля в центре
соленоида,
:
,
из геометрических соображений:
,
тогда
или
. (8.4)
2. Методика выполнения работы
В данной работе для изучения магнитного
поля соленоида используется индукционный
датчик, наводимая э.д.с. в котором прямо
пропорциональна амплитуде переменного
магнитного поля
~
В. Индукционный датчик необходимо
проградуировать. Для этого следует
найти коэффициент пропорциональности
(постоянную датчика) между э.д.с.
индукционного датчика
и величиной индукции магнитного поля
.
С этой целью индукционный датчик
устанавливается в центре соленоида,
где неоднородность магнитного поля
наименьшая. Меняя ток соленоида
(соответственно меняя
),
измеряют
.
Рассчитав по формуле (8.4) индукцию
магнитного поля в центре соленоида
,
строят градуировочный график зависимости
э.д.с. датчика
от индукции
.
Из него определяют постоянную индукционного
датчика.
Затем установив в соленоиде некоторое
значение тока и перемещая индукционный
датчик вдоль оси соленоида, фиксируют
его положение
на рейтере и измеряют
.
Далее по градуировочному графику каждому
значению
ставят в соответствие значение
и строят график зависимости
(
).
Таким образом получают кривую распределения
индукции магнитного поля вдоль оси
соленоида.