vk.com/club152685050 | vk.com/id446425943
где gz – удельная энергия положения;
– удельная энергия давления движущейся жидкости;
– удельная кинетическая энергия.
Мы видим, что последнее уравнение – это уравнение закона сохранения механической энергии.
Если это уравнение домножить еще и на r, то получим уравнение Бернулли, записанное через давления:
где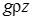 
– весовое давление;
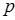– гидромеханическое давление;
– динамическое давление.
Уравнение Бернулли для элементарной струйки реальной жидкости.
Для реальной жидкости равенство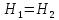 
нарушается, и вместо него имеем
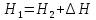, где
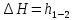– потеря напора на участке 1–2. Тогда для элементарной струйки реальной жидкости уравнение Бернулли примет вид
Таким образом, полный напор вдоль струйки реальной жидкости уменьшается. Для характеристики относительного изменения полного напора на единицу длины вводится понятие о гидравлическом уклоне
Например, на участке трубопровода 1–2
где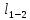 
– длина участка 1–2.
vk.com/club152685050 | vk.com/id446425943
Таким образом, гидравлическим уклоном называется отношение потери напора к длине, на которой она происходит. Кроме того, вводится еще понятие о пьезометрическом уклоне
30. Геометрический, физический и энергетический смысл уравнения Бернулли
Сформулируем геометрический смысл уравнения Бернулли.
При установившемся движении жидкости элементарной струйки сумма трех высот есть величина постоянная вдоль элементарной струйки.
Уравнение Бернулли (2.68) выражает один из случаев закона сохранения энергии в любом сечении элементарной струйки.
Таким образом, энергетический смысл уравнения Бернулли заключается в следующем: при установившемся движении жидкости элементарной струйки сумма трех удельных энергий (энергии положения, энергии давления и кинетической энергии) остается неизменной вдоль элементарной струйки. В уравнении Бернулли (2.66) можно слагаемые рассматривать как удельные энергии, но уже по отношению к единице веса жидкости.
31.Гидравлический уклон
Гидравлическим уклоном называют отношение потери напора на трение к единице длины трубопровода (рис. 2.2):
i = hтp/l = h/ l = lu2 /2d,
где u - скорость; d – внутренний диаметр трубопровода; l - коэффициент трения; hтр - напор, потерянный на трение; l - длина трубопровода. hтри l имеют одинаковую размерность, поэтому i - безразмерная величина.
Рис. 1.7. Графическое представление линии гидравлического уклона
Как видно из рисунка, линия гидравлического уклона показывает распределение напора по длине трубопровода. Напор в любой точке трассы определяется вертикальным отрезком, отложенным от линии профиля трассы до пересечения с линией гидравлического уклона. При графических построениях
(расстановке ПС на профиле трассы) положение линии гидравлического уклона должно учитывать надбавку на местные сопротивления.
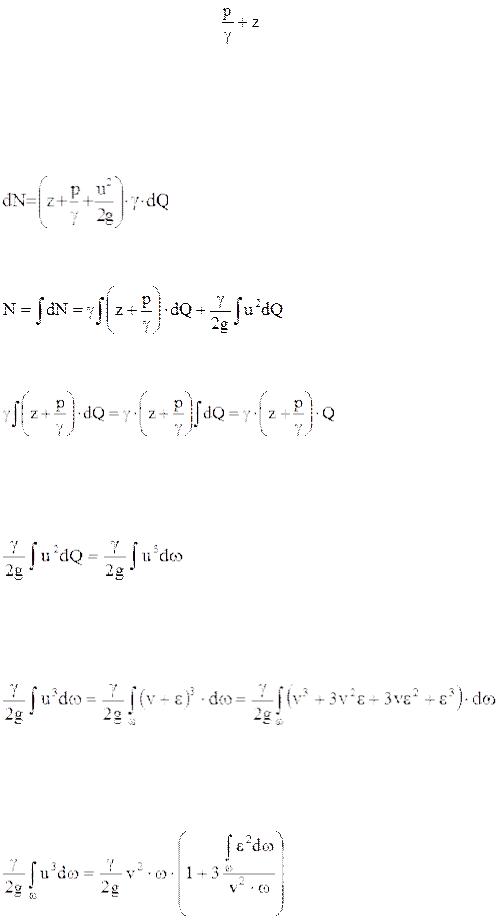
vk.com/club152685050 | vk.com/id446425943
32.Уравнение для потока жидкости с поперечным сечением конечных размеров
В этих условиях распределение давления по поперечному сечению следует закону
гидростатики, то есть величина |
одинакова для всех точек сечения потока. |
Введём понятие мощности потока: мощность потока в данном сечении – это энергия, которую проносит поток через это сечение в единицу времени.
Рассмотрим поток как совокупность элементарных струек. Запишем выражение для мощности каждой элементарной струйки:
Мощность всего потока найдется интегрированием по площади поперечного сечения:
С учетом того, что поток меняется плавно, первый интеграл приводим к следующему виду:
Второе слагаемое рассмотрим подробнее.
Так как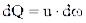 
, то можно записать:
Местную скорость u можно представить в виде: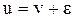 
, где v – средняя скорость, а 
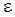- разность между средней и местной скоростью (может быть положительной, отрицательной или равной нулю). Сделав подстановку, получим:
Если учесть, что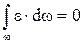 
и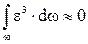 
, так как величина 
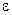очень мала и для разных точек сечения имеет различные знаки, то после перегруппировки мы получим следующее выражение:
Обозначим для краткости выражение в скобках как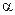 
и запишем для кинетической энергии потока выражение:
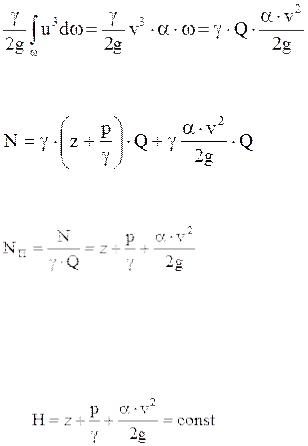
vk.com/club152685050 | vk.com/id446425943
Врезультате для мощности всего потока имеем:
Отсюда удельная мощность потока:
Уравнение Бернулли для потока идеальной жидкости:
,
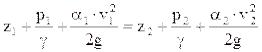или
Таким образом, уравнение Бернулли для потока отличается от такового для элементарной струйки тем, что здесь скоростной напор дополнен коэффициентом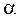 
, носящим название коэффициента Кориолиса.
Величина этого коэффициента зависит от степени неравномерности распределения скорости по
сечению потока. Он всегда больше 1-цы за исключением случая, когда местные скорости равны между собой и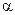 
=1. Для ламинарного течения в круглых трубах 
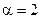, для турбулентного течения коэффициент Кориолиса принимает значение в пределах 
.
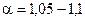Для расчета простых по сечению трубопроводов можно принимать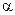 
=1.
34. Виды гидравлических сопротивлений
Сопротивления, возникающие по длине потока жидкости, - сопротивления по длине. Местными сопротивлениями называются участки потока жидкости, в которых происходит достаточно резкая деформация и средняя скорость изменяется по значению и направлению.
35. Режимы течения жидкости в трубах
Возможны два режима течения жидкостей в трубах: ламинарный и турбулентный.
Ламинарным называют слоистое течение жидкости без перемешивания её частиц и без пульсаций скоростей и давлений. Частицы жидкости при таком режиме движутся параллельно стенкам трубопровода.
Турбулентным называют течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. Движение частиц жидкости при таком режиме приобретает беспорядочный характер.