vk.com/club152685050 | vk.com/id446425943

22. Закон Архимеда

Зако́н Архиме́да — один из законов статики жидкостей (гидростатики) и газов (аэростатики): на тело, погружённое в жидкость или газ, действует выталкивающая или подъёмная сила Pa, равная по величине весу жидкости в объеме погруженной части тела V. Закон открыт Архимедом в III веке до н. э. Выталкивающая сила также называется архимедовой или гидростатической подъёмной силой[1][2].

В соответствии с законом Архимеда для выталкивающей силы выполняется[3]:

Pa= g*v

где:

—плотность жидкости или газа, кг/м3;

—ускорение свободного падения, м/с2;

—объём части тела, погружённой в жидкость или газ, м3;

—сила Архимеда, Н.

23. Методы исследования движения жидкости

В гидромеханике существуют два метода изучения движения жидкости: метод Лагранжа и метод Эйлера.

1. Метод Лагранжа заключается в изучении движения каждой отдельной частицы жидкости. В этом случае движение определяется положением частицы жидкости в функции от времени t. Движение частицы будет определено, если точно определить координаты x, y, и z в заданный момент времени t, что дает возможность построить траекторию движения частицы жидкости. Величины x, y, и z являются переменными Лагранжа, а их изменения за время dt позволяет

Учитывая, что для установления движения линии тока совпадают с траекторией движущихся частиц,

можно записать =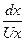

Это выражение называется уравнением линии тока. Метод Лагранжа в гидравлике не нашел

vk.com/club152685050 | vk.com/id446425943

Широкого применения ввиду его относительной сложности.

2. Метод Эйлера основан на изучении поля скоростей, под которым понимается значение величины и скоростей во всех точках пространства, занятого движущейся жидкостью.

Переменными Эйлера являются значения скоростей 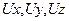, которые определяются в зависимости от координат точек пространства и времени, т. е.

Метод Эйлера нашел широкое применение в гидравлике. Он позволяет определить скорость в любой момент времени, но в то же время не позволяет изучить движение отдельной частицы жидкости.

Рассмотрим теперь понятие расхода жидкости и средней скорости.

Расходом Q называется количество жидкости, протекающее через сечение потока в единицу времени.

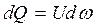или

Средней скоростью называется одинаковая по всему сечению потока скорость, при которой расход равен действительному.

Средней скоростью в данном живом сечении потока называется такая фиктивная, но одинаковая во всех точках сечения величина, при которой через данное сечение проходит такое, же количество жидкости, как и при действии распределенных скоростей.

24. Линии и труба тока, элементарная струйка, поток, локальные и средние скорости

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока - трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока,

называется элементарн ой струйкой.

Так как в потоке скорость отдельных частиц жидкости различна по живому сечению не всегда

известен. Понятие средней скорости v в сечении. Средняя скорость v в сечении потока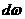- такая фиктивная скорость, с которой должны были двигаться все частицы жидкости, чтобы при этом

объемный расход Q был бы тем же, что при реальном распределении скоростей.

Локальная скорость потока - это скорость в определенной точке потока, измеряющаяся трубкой Пито-Прандтля.

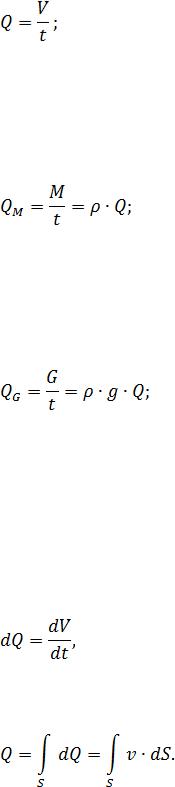
vk.com/club152685050 | vk.com/id446425943

25. Уравнение расхода жидкости

Расход жидкости – количество жидкости, протекающей в единицу времени через живое сечение потока.

Различают объёмный, массовый и весовой расходы жидкости.

Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м3/с, л/с. Он вычисляется по формуле

где Q - объёмный расход жидкости,

V - объём жидкости, протекающий через живое сечение потока,

t – время течения жидкости.

Массовый расход жидкости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле

где QM - массовый расход жидкости,

M -масса жидкости, протекающий через живое сечение потока,

t – время течения жидкости.

Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, кН/с. Формула для его определения выглядит так:

где QG - весовой расход жидкости,

G - вес жидкости, протекающий через живое сечение потока,

t – время течения жидкости.

Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости dQ.

Расход элементарной струйки – объем жидкости dV, проходящей через живое сечение струйки в единицу времени. Таким образом:

Если последнее выражение проинтегрировать по площади живого сечения потока м ожно получить формулу объёмного расхода жидкости, как сумму расходов элементарных струек

Применение этой формулы в расчетах затруднительно, так как расходы элементарных струек жидкости в разлчных точках живого сечения потока различны. Поэтому чаще используют среднюю

скорость потока .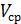

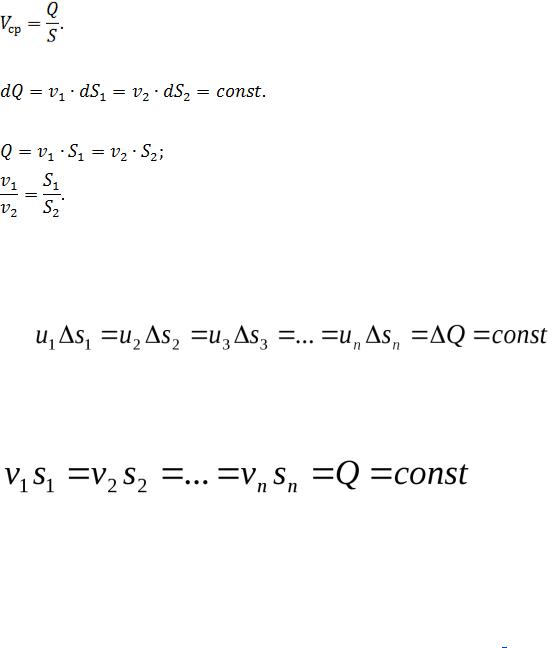
vk.com/club152685050 | vk.com/id446425943

Уравнения объемного расхода во всех сечениях элементарной струйки

Аналогичные уравнения можно составить и для потока конечных размеров

Это уравнения неразрывности потока капельной жидкости.

26. Уравнение неразрывности

уравнение неразрывности для потока жидкости, которое читается так: расход жидкости через любое сечение потока при установившемся движении есть величина постоянная.

Уравнение неразрывности потока демонстрирует закон сохранения массы: количество втекающей и вытекающей жидкости неизменно.

Проанализируем сечение 1 с площадью и скоростью движения частиц жидкости обозначим и1. Эл ементарный расход для него представлен соотношением:

Q1 = u1w1.

Далее проанализируем сечение 2 в этой же струйке с площадью сечения и скоростью обозначим и2. Элементарный расход для него представлен соотношением:

Q2 = u2w2.

Но согласно характерной особенности элементарной струйки притока и оттока жидкости через ее боковую поверхность не существует; на промежутке 1 - 2, которому свойственны постоянные размеры, отсутствуют пустоты и отсутствуют переуплотнения количества жидкости, протекающей в единицу времени сквозь сечения 1 и 2,будут одинаковыми, тогда:

Q1 = Q2 = const.

27. Ламинарный и турбулентный режим течения вязкой жидкости