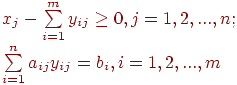Задача о наилучшем распределении памяти вычислительной машины

Рассмотрим следующую упрощенную задачу о наилучшем распределении памяти вычислительной машины. Пусть — -я стандартная подпрограмма для вычисления функции в библиотеке подпрограмм . Подпрограмма занимает ячеек памяти и требует для счета секунд. Требуется составить "программу" , которая определяется заданием некоторого набора индексов , то есть функций, подлежащих вычислению (наличием иных команд пренебрегаем). При этом следует для составления программы указать такой набор подпрограмм , чтобы длина всей программы не превосходила M ячеек, а время счета по ней было минимальным.

Как обычно в подобных случая, вводим переменные

(7.33)

Тогда наша задача сведется к минимизации

(7.34)

при условиях

(7.35)

Задача финансирования исследовательских проектов

Рассмотрим финансирование исследовательских проектов. Пусть на протяжении лет возможно осуществление исследовательских проектов. Ожидаемый эффект проекта , выраженный в "сегодняшних" единицах полезности, составляет . Затраты в год на осуществление проекта составляют , а общий лимит капиталовложений на исследования в году равен . Требуется указать максимально эффективный набор проектов, не выводящий за пределы отпускаемых вложений.

Формализация этой задачи очевидна: если обычным образом ввест переменные

(7.36)

то мы придем к задаче максимизации

при условиях

(7.37)

Задача из области экономики сельского хозяйства

Рассмотрим следующую упрощенную статическую модель распределения тракторных работ (Корбут А.А. Целочисленные задачи линейного программирования. В сб. "Эконом.-матем. методы", вып. 2, М., "Наука", 1965, 141-186.).

Имеется n типов сельскохозяйственных машин и m видов работ, подлежащих выполнению в объемах , (будем считать, что все эти объемы выражены в гектарах). Заданы производительность -й машины на -й работе , а также себестоимость обработки одного гектара работы машиной . Себестоимость самих машин (скажем, стоимость их покупки или аренды, взятая с некоторым коэффициентом приведения) составляет . Следует найти оптимальный машинный парк для данного комплекса работ и указать его распределение по работам. Чтобы выполнить задание и добиться минимальной суммарной себестоимости, обозначим через количество машин каждого типа, а через — количество машин типа , которое будет выделено на работу . Тогда наша задача сведется к минимизации

(7.38)

при условиях

(7.39)

(7.40)

Отметим, что накладывать условие целочисленности на не обязательно, так как нецелые здесь вполне поддаются разумной интерпретации.

Таким образом, перед нами еще один пример задачи с неделимостями. Модель эта существенно усложнится, если дополнительно потребовать выполнения каждой работы в отведенные для нее агротехнические сроки; здесь мы не будем на этом останавливаться.