Количество решений задачи, решаемой графическим методом.

1

Рис. 2.2

. Единственное решение: опорная прямая не параллельна прямым, содержащим точку «выхода».

2

Рис. 2.3

. Бесконечное множество оптимальных решений: опорная прямая параллельна одной из прямых, содержащих точку «выхода». Например, максимум достигается в любой точке отрезка АВ (рис. 2.2).

3. Оптимальное решение не достигается: не существует точки «выхода» из ОДР (рис. 2.3).

Пример. Найдем оптимальное решение в задаче о производстве столов и стульев.

1. Найдем область допустимых решений, для этого построим прямые и определим полуплоскости − решения неравенств (рис. 2. 4).

Рис. 2.4

2х₁ +0,5х₂= 80; (1)

х₂ = 4х₁; (2)

х₂ = 6х₁; (3)

х₁ =0; х₂ = 0.

2. Построим опорную прямую 135х₁ + 50х₂= 0 и вектор градиент целевой функции grad F = (135; 50).

На рис. 2.4 указан вектор направленный по градиенту grad F.

Угол между прямой (1) и осью ОХ, больше угла наклона между опорной прямой и осью ОХ, следовательно, точкой «выхода» будет точка А.

3. Найдем координаты точки А, как решение системы:

Итак, для того чтобы прибыль от производства столов и стульев была максимальной каждый столяр за 10 дней должен произвести 96 стульев и 16 столов.

Замечание.Задачи линейного программирования не могут быть решены методами оптимизации, применяемыми в математическом анализе, т.к. первая производная линейной функции равна постоянной величине и, следовательно, не содержит неизвестного параметра для последующего его определения.

§ 2.2. Графический метод решения задачи линейного программирования (случай n переменных)

Задачу линейного программирования можно свести к задаче, решаемой графическим методом, если она задана в канонической форме, либо после приведения ее к канонической форме, и разность между количеством переменных n и количеством неизвестных m равна двум.

В этом случае существует возможность выразить m базисных неизвестных через 2 оставшиеся свободные и, учитывая неотрицательность переменных, перейти от системы уравнений к системе неравенств с двумя неизвестными.

Иными словами это означает, что в семействе векторов с координатами, состоящими из коэффициентов при соответствующих переменных, необходимо выделить базис или найти общее решение системы.

Проиллюстрируем применение этого метода на примере.

Пример. Найдите план, минимизирующий значение функции

, при заданных ограничениях х_i 0, i =1, 2,…,5:

Данную задачу можно решить графическим методом, так как выполняется условие n – m = 2. Действительно, в системе ограничений число неизвестных 5, число уравнений 3.

Составим расширенную матрицу системы:

.

Выберем в качестве базисных переменных х₁, х₂, х₃. Следовательно, первые три столбца матрицы должны представлять собой единичную матрицу.

Проведем преобразование методом Гаусса: прибавим ко второй и к третьей строкам первую, умноженную на –1.

 .

Последняя матрица получена прибавлением к третьей строке второй, умноженной на 5. Разделим третью строку на –12.

.

Для того чтобы первые три столбца образовали единичную матрицу, применим преобразование Гаусса «снизу вверх». Прибавим к первой строке третью, умноженную на –3, а ко второй строке – третью, умноженную на 2.

 .

Последняя матрица получена прибавлением к первой строке второй, умноженной на –2.

По преобразованной матрице составим систему уравнений:

Выразим базисные переменные через свободные х₄, х₅.

(2.4)

Учтем, что все переменные неотрицательны, следовательно, правые части уравнений так же больше или равны нулю. Получим систему неравенств с двумя неизвестными.

(2.5)

Используя соотношения системы (2.4), выразим целевую функцию через свободные переменные.

,

.

Найдем область решений системы (2.5) графически. Построим прямые и определим полуплоскости – решения каждого неравенства (рис. 2.5).

Рис. 2.5

Построим опорную прямую z = 5;

Вектор с на рис. 2.5 направлен по градиенту целевой функции и указывает направление ее роста, следовательно, в противоположную сторону целевая функция будет убывать. Точка «входа» в ОДР – точка О(0,0), точки «выхода» не существует. Подставим координаты точки «входа» в целевую функцию и получим ее минимальное значение z = 5. Вычислим значения базисных переменных в точке «входа», учитывая (2.4), их значения равны: х₁ = 2; х₂ = 1; х₃ = 2.

Итак, минимальное значение целевой функции z = –5, это значение достигается на оптимальном плане (2; 1; 2; 0; 0).

Продолжим рассмотрение практических задач, для решения которых требуется составление математических моделей.

Пример. Завод производит три типа (I, II, III) некоторого изделия, используя для этого сырье А и В. На изготовление единицы изделия типа I затрачивается в два раза больше рабочего времени, чем на изготовление единицы изделия типа II и в столько же, сколько на изготовление изделия типа III. Рабочие ресурсы завода эквивалентны ресурсам, необходимым на изготовление 1500 шт. изделия типа I. Данные о расходе материалов приведены в таблице. Руководство завода приняло решение ликвидировать склад для хранения сырья А и стремится организовать производство таким образом, чтобы, израсходовав сырье А, полностью получить наибольший доход. Каков должен быть план производства?

	Нормы расхода сырья на 1 изделие
Тип сырья	I	II	III	Запасы сырья
А	2	3	5	4000
В	4	2	7	6000
Доход на 1ед.	30	20	50

Составим математическую модель задачи.

1. Критерием эффективности является доход от производства, стремящийся к максимуму.

2. Параметрами управления являются х₁ – количество изделий типа; х₂ – количество изделий типа II; х₃ – количество изделий типа III.

3. Составим систему ограничений: ограниченными являются ресурсы времени и запасы сырья А и В.

Пусть а – затраты времени на производство одного изделия I, тогда 0,5 а  затраты времени на производство одного изделия II, следовательно, и, следовательно,

.

В связи с тем, что сырье А необходимо израсходовать полностью, ограничение на его запас имеет вид:

.

Ограничение на запас сырья В имеет вид:

.

4. Целевая функция – доход стремится к максимуму на системе ограничений.

5. Выберем метод решения задачи оптимизации по виду математической модели:

Приведем задачу линейного программирования к каноническому виду.

Переменные х₄ играет роль остатка сырья В, а х₅ – роль оставшегося рабочего времени.

Число неизвестных системы на два больше числа уравнений, следовательно, задача может быть решена графически.

Запишем матрицу системы и выберем базисные переменные.

.

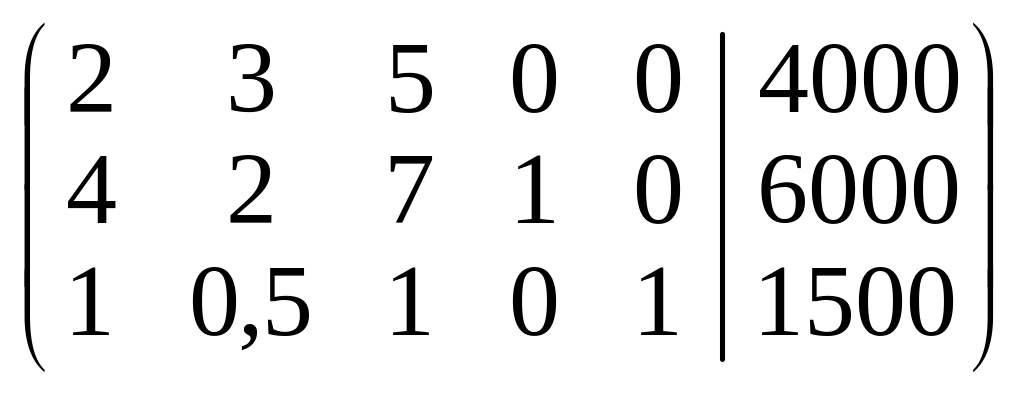В качестве базисных удобно выбрать переменные х₁, х₄, х₅. Преобразуем матрицу, разделив первую строку на 2.

 .

Последняя матрица получена прибавлением к третьей строке первой, умноженной на –1, и ко второй – первой, умноженной на –4.

По равносильной расширенной матрице системы составим систему уравнений.

Найдем общее решение системы. Выразим базисные переменные через свободные:

(2.6)

Учитывая неотрицательность левых частей уравнений, можем перейти к системе неравенств с двумя неизвестными.

(2.7)

Подставим в целевую функцию выражения (3.6):

Решим получившуюся задачу графически. Построим ОДР системы (2.7). Проведем опорную прямую L, приравняв F = 60000. Ее уравнение после преобразований х₂ + х₃ = 0, grad F = (25; 25). Все построения приведены на рис. 3.6.

В

Рис. 2.6

выделенном многоугольнике решений точкой «выхода» в направлении вектора-градиента целевой функции является точка с координатами х₂ = 500, х₃=0. Значение целевой функции в этой точке:

F = 25500 + 60000 = 47500.

Подставим значения переменных в (2.6), получим х₁ = 750, х₄ = 0; х₅ = 0.

Итак, для получения наибольшего дохода в количестве 47500 д.е. при заданных условиях необходимо производить 750 ед. продукции типа I, 500 ед. продукции типа II и не производить продукцию типа III, при этом все ресурсы и сырьевые и временные будут израсходованы полностью.