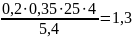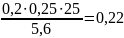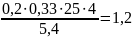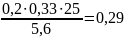3.3.1 Расчет балки по нормальному сечению
Первый пролет:
Предполагаем,
что нейтральная ось проходит по нижней
грани полки, определяем область
деформирования для прямоугольного
сечения с шириной
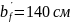 и положение нейтральной оси при расчете
тавровых сечений.
и положение нейтральной оси при расчете
тавровых сечений.
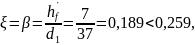 что
указывает на то, что сечение находится
в области деформирования 1б.
что
указывает на то, что сечение находится
в области деформирования 1б.
С помощью таблиц находим величину изгибающего момента, воспринимаемого бетоном сечения, расположенным в пределах высоты норм, т.е.:

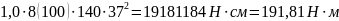 .
.
Поскольку
выполняется условие:
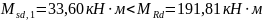 ;
нейтральная ось расположена в пределах
полки. В связи с этим дальнейший расчет
производится как прямоугольного сечения
имеющие размеры
;
нейтральная ось расположена в пределах
полки. В связи с этим дальнейший расчет
производится как прямоугольного сечения
имеющие размеры
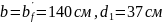 .
.
Определяем:
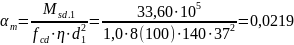
По
табл. 6.7 по
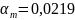 определяем η =0,974. Находим величину
требуемой площади растянутой арматуры:
определяем η =0,974. Находим величину
требуемой площади растянутой арматуры:
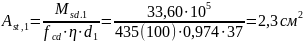
Принимаем
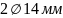 из арматуры класса S500, с площадью
из арматуры класса S500, с площадью
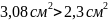 .
.
Второй пролет:
Предполагаем,
что нейтральная ось проходит по нижней
грани полки и определяем область
деформирования для прямоугольного
сечения с шириной
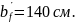
 что
указывает на то, что сечение находится
в области деформации 1б.
что
указывает на то, что сечение находится
в области деформации 1б.
По формуле, табл. 6.6 находим величину изгибающего момента воспринимаемого бетоном в сечении, расположенным в пределах высоты полки:
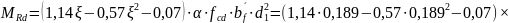
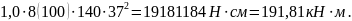
Поскольку
выполняется условие:
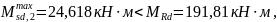 значит нейтральная ось расположена в
пределах полки. В связи с этим дальнейший
расчет производится как прямоугольного
сечения имеющие размеры
значит нейтральная ось расположена в
пределах полки. В связи с этим дальнейший
расчет производится как прямоугольного
сечения имеющие размеры
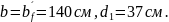
Определяем:
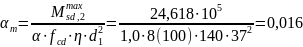
По
табл. 6.7 по
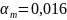 определяем
определяем
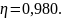 Находим величину требуемой площади
растянутой арматуры:
Находим величину требуемой площади
растянутой арматуры:
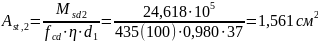
Принимаем
из арматуры класса S500,
с площадью
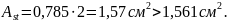
- на опоре «В»:
Принимаем
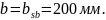 Определяем величину коэффициента
:
Определяем величину коэффициента
:
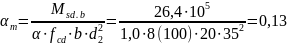
Определяем относительную деформацию арматуры по пределу текучести:
Тогда:
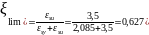
Определяем относительную деформацию арматуры по пределу текучести. Определяем граничную величину коэффициента
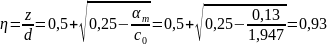
Поскольку
условие выполняется
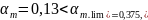 тогда требуемая площадь арматуры
составит:
тогда требуемая площадь арматуры
составит:
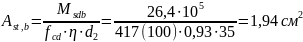
Принимаем
2 сетки марки
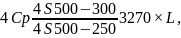 с площадью
с площадью
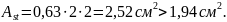
- на опоре «С»:
Принимаем Определяем величину коэффициента :
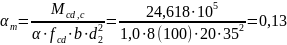
Определяем относительную деформацию арматуры по пределу текучести:
Тогда:
Определяем граничную величину коэффициента
Поскольку
условие выполняется
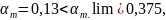 тогда требуемая площадь арматуры
составит:
тогда требуемая площадь арматуры
составит:
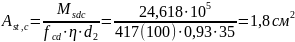
Принимаем2
сетки марки
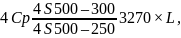 с площадью
с площадью
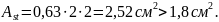
Отрицательный
изгибающий момент может отсутствовать
также и в промежуточном сечении пролета.
В этом случае балки находятся в растянутой
зоне
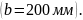 Тогда расчет производим с помощью
таблиц, как для балки прямоугольного
сечения. Для чего определяем:
Тогда расчет производим с помощью
таблиц, как для балки прямоугольного
сечения. Для чего определяем:
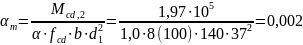
По
вычисленному
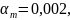 находим коэффициент
находим коэффициент
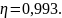 Тогда:
Тогда:
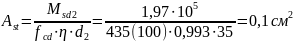
Принимаем
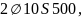 с площадью
с площадью
3.3.2 Расчет прочности по наклонному сечению
Определение поперечных сил.
- на опоре «А» и «К»

- на опоре «В» (слева) и опоре «Е» (справа):
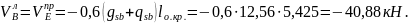
- на опоре «В» (справа) и на всех остальных опорах слева и справа:
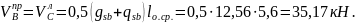
Расчет
ведем на максимальное значение поперечной
силы
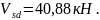
Для типизации каркаса изготавливают с одинаковым расположением поперечной арматуры во всех пролетах второстепенной балки.
Расчет прочности железобетонных элементов на действие поперечных сил, в которых отсутствует вертикальная арматура, согласно требованиям норм следует производить из условия:
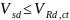
где
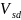 – расчетная поперечная сила в
рассматриваемом сечении, вызванная
действием нагрузок;
– расчетная поперечная сила в
рассматриваемом сечении, вызванная
действием нагрузок;
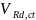 – поперечная
сила, воспринимаемая элементом без
вертикальной арматуры, и определяемая
по формуле:
– поперечная
сила, воспринимаемая элементом без
вертикальной арматуры, и определяемая
по формуле:

но не менее
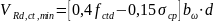 ,
,
где
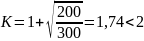 ,
d
в мм
,
d
в мм
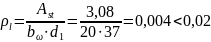
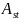 – площадь
сечения продольной растянутой арматуры,
учитывается в расчете, при условии, что
она заведена за расчетное сечение на
длину не менее d
и надежно заанкерована. Из конструктивных
требований принимаем
– площадь
сечения продольной растянутой арматуры,
учитывается в расчете, при условии, что
она заведена за расчетное сечение на
длину не менее d
и надежно заанкерована. Из конструктивных
требований принимаем
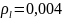 .
.
Расчетное сопротивление бетону:
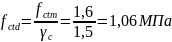
где
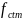 – средняя прочность бетона на осевое
растяжение.
– средняя прочность бетона на осевое
растяжение.
Тогда:
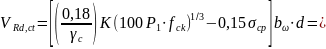

 .
.
Так
как
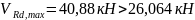 ,
значит поперечная арматура требуется
по расчету.
,
значит поперечная арматура требуется
по расчету.
Задаемся
углом наклона трещин к горизонтали
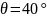 .
.
В пределах длины расчетного участка поперечное армирование рассчитывается из условия:
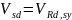 ;
;
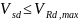
где:
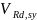 – расчетная поперечная сила, воспринимаемая
сечением с поперечным армированием.
– расчетная поперечная сила, воспринимаемая
сечением с поперечным армированием.
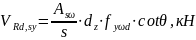
Задавшись
шагом поперечной арматуры определяем
площадь ее сечения по последней формуле,
учитывая то, что в данном методе количество
поперечной арматуры рассчитывают приняв
условие, что напряжение в ней достигают
предела текучести:
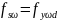 .
.
Принимаем
шаг поперечной арматуры
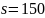
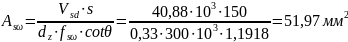
Принимаем
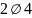 класса S500,
площадью
класса S500,
площадью
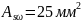 .
.
При этом должно выполняться следующее условие:
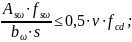
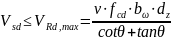
где: v – коэффициент, учитывающий снижение прочности бетона при сжатии в условиях растяжения и равный для тяжелого бетона:
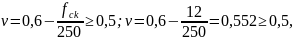 значит
принимаем
значит
принимаем
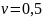 .
.
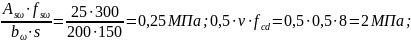
0,25 < 2 – условие выполняется.
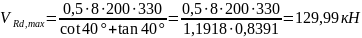
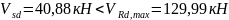
Окончательно
принимаем поперечные стержни из арматуры
класса S500
диаметром 4 мм, с шагом
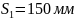 ,
а в средней части пролета
,
а в средней части пролета
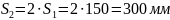 ,
что удовлетворяет требованиям СНБ (п.
11,2.21 стр. 106).
,
что удовлетворяет требованиям СНБ (п.
11,2.21 стр. 106).
4 Расчет колонны и фундаментов под колонны
4.1 Расчет колонны
В данном курсовом проекте колонны и фундаменты предусмотрены сборными. Колонны, установленные для изготовления перекрытия, служат несущими элементами опалубки. В них предусматриваются выпуски арматурных стержней для создания неразрезности главных и второстепенных балок. Кроме того, в гранях колонны предусмотрены ниши, создающие бетонную шпонку и ориентирующие опалубку.
Колонну рассчитываем как работающую со случайным эксцентриситетом, так как изгибающий момент от поворота опорных сечений, связанных с колонной главных балок незначительно (нагрузка практически симметрична относительно оси колонны). Нагрузка на колонну складывается из нагрузок покрытия и перекрытия, а также собственного веса. Для определения нагрузки задаемся следующей конструкцией покрытия (рисунок 4.1).

Утеплитель - пенополистерол 140 мм
Рис. 4.1 – Состав покрытия
Переменная нагрузка на перекрытие принимается в зависимости от района строительства. В данном случае для г. Чечерск нормативное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли sо = 1,2 кН/м2 при = 1,5 (IIБ район).
Подсчет нагрузки на 1 м2 покрытия и перекрытия сводим в таблицу 4.1.
Таблица 4.1 – Нормативные и расчетные нагрузки
Вид нагрузки |
Нормативная нагрузка, кН/м2 |
|
Расчетная нагрузка, кН/м2 |
От покрытия 1 Постоянная 1.1 Верхний слой – изопласт с посыпкой массой m = 3 кг/м2 1.2 Два нижних слоя без посыпки m = 4 кг 1.3 Огрунтовка битумно-кикурсольной мастикой за 1 раз δ = 1 мм, ρ = 1100 кг/м3 1.4 Цементно-песчаная стяжка δ = 20 мм, ρ = 1800 кг/м3 1.5 Утеплитель пенополистирол δ = 140 мм, ρ = 35 кг/м3 1.6 Пароизоляция – из одного слоя рубероида на мастике δ = 1,5 мм, ρ1 = 600 кг/м3 δ = 2 мм, ρ2 = 1200 кг/м3 1.7 Железобетонная плита покрытия δ = 50 мм, ρ = 2500 кг/м3 1.8 Железобетонная второстепенная балка bsb = 200 мм hsb = 350 мм ρ = 2500 кг/м3 l = 5,800 - 0,4 = 5,4 м 1.9 Железобетонная второстепенная балка bmb = 200 мм hmb = 250 мм ρ = 2500 кг/м3 l = 5600 мм |
0,03 0,04
0,001∙11 = 0,011
0,02∙18 = 0,36
0,14∙0,35 = 0,049
0,0015∙6 = 0,009 0,002∙12 = 0,024
0,05∙25 = 1,25
|
1,5 1,35
1,35
1,35
1,35
1,35 1,35
1,35
1,35
1,35 |
0,04 0,108
0,015
0,486
0,066
0,012 0,032
1,69
1,75
0,30 |
Продолжение таблицы 4.1
1 |
2 |
3 |
4 |
Всего |
3,293 |
- |
4,499 |
2 Переменная (снеговая) |
1,2 |
1,5 |
1,8 |
Итого |
4,493 |
- |
6,299 |
От перекрытия 1 Постоянная 1.1 Керамическая плитка δ = 15 мм, ρ = 2000 кг/м3 1.2 Мастика δ = 1 мм, ρ = 1000 кг/м3 1.3 Цементно-песчаная стяжка δ = 30 мм, ρ = 1800 кг/м3 1.4 Звукоизоляция из ДВП δ = 32 мм, ρ = 250 кг/м3 1.5 Монолитная плита δ = 70 мм, ρ = 2500 кг/м3 1.6 Железобетонная второстепенная балка bsb = 200 мм hsb = 330 мм ρ = 2500 кг/м3 l = 5,800 - 0,4 = 5,4 м 1.7 Железобетонная второстепенная балка bmb = 200 мм hmb = 330 мм ρ = 2500 кг/м3 l = 5600 мм |
0,015∙20 = 0,3
0,001∙10 = 0,01
0,03∙18 = 0,54
0,32∙25 = 0,08
0,07∙25 = 1,75
|
1,35
1,35
1,35
1,35
1,35
1,35
1,35 |
0,405
0,135
0,729
0,108
2,362
1,65
0,4 |
Всего |
4,19 |
- |
5,668 |
2 Переменная |
3,0 |
1,5 |
4,5 |
Итого |
7,19 |
- |
10,168 |
Нагрузка на один квадратный метр перекрытия от собственного веса: перекрытия составляет – 5,668 кН/м2; покрытия – 4,499 кН/м2. Переменная (полезная) нагрузка на перекрытие составляет – 4,5 кН/м2; переменная нагрузка на покрытие (снеговая) – 1,8 кН/м2.
Грузовая площадь колонны:
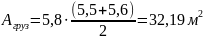
Тогда:
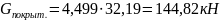
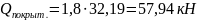
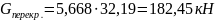
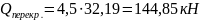
Собственный вес колонны в пределах первого этажа:
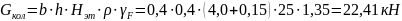 .
.
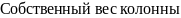 в
пределах последующих этажей:
в
пределах последующих этажей:
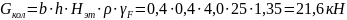 .
.
Определяем усилие в колонне в пределах первого этажа:
- от постоянных нагрузок:
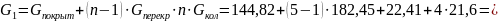
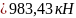
- от переменных:
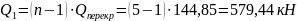 ;
;
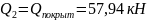 .
.
Составим расчетные усилия:
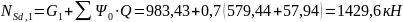 ;
;
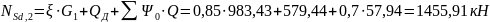
где
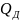 – доминирующая переменная нагрузка.
– доминирующая переменная нагрузка.
Наиболее
выгодным является второе сочетание –
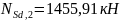 .
.
Практически
постоянную часть усилия от переменной
нагрузки определим путем умножения
полного значения переменной нагрузки
на коэффициент сочетания
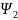 (зависит от вида нагрузки), определяемой
по таблице А.1 приложения А СНБ 5.03.01-02
«Бетонные и железобетонные конструкции»
(зависит от вида нагрузки), определяемой
по таблице А.1 приложения А СНБ 5.03.01-02
«Бетонные и железобетонные конструкции»
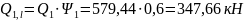 ;
;
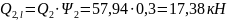 .
.
Выберем часть продольной силы при практически постоянном сочетании нагрузок для второй комбинации:
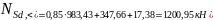 .
.
Таким образом,
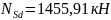 – полное
усилие в колонне первого этажа,
– полное
усилие в колонне первого этажа,
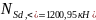 – усилие
при практически постоянном сочетании
нагрузок в колонне первого этажа.
– усилие
при практически постоянном сочетании
нагрузок в колонне первого этажа.
Расчетную длину колонны определяем по формуле
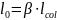 ,
,
где
 – коэффициент, зависящий от характера
закрепления концов стойки.
– коэффициент, зависящий от характера
закрепления концов стойки.
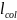 – геометрическая
длина колонны
– геометрическая
длина колонны
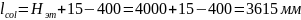
где
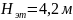 – высота этажа по заданию;
– высота этажа по заданию;
400 – Высота сечения главной балки, мм;
-0,015 – отметка обреза фундамента, м.
Случайный эксцентриситет составит:
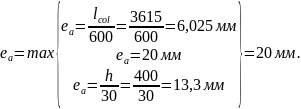
Определяем гибкость колонны и необходимость учета влияния продольного изгиба:
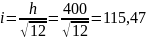 мм.
мм.
 ,
следовательно, необходимо учитывать
влияние продольного изгиба.
,
следовательно, необходимо учитывать
влияние продольного изгиба.
Определяем эффективную расчетную длину:
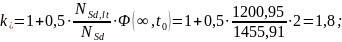
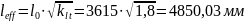 .
.
Определяем
гибкость
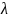 через
h:
через
h:
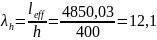
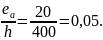
Для изготовления колонны принимаем следующие материалы:
- продольная рабочая арматура класса S500, для которой:
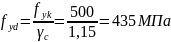 при
диаметре 6 – 22 мм;
при
диаметре 6 – 22 мм;
-
бетон тяжелый класса С20/25
для которого
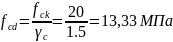 .
.
По
табл. СНБ при
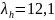 и
и
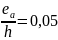 величина коэффициента
величина коэффициента
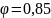 .
.
Из
условия
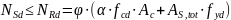 площадь арматуры, требуемая по расчету
площадь арматуры, требуемая по расчету
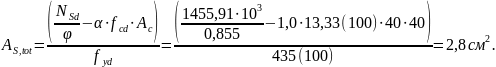
Для
армирования колонны и принимаем
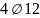 класса S500
класса S500
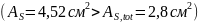 .
.
Коэффициент продольного армирования колонны (табл. 11.1)
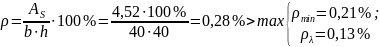
где
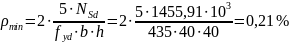 ;
;
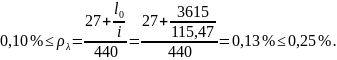
Тогда
несущая способность сечения составит
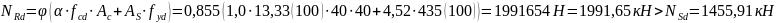 ,
условие выполняется.
,
условие выполняется.
Принимаем поперечные стержни из арматуры класса S240 диаметром 6 мм с шагом s = 200 мм, что удовлетворяет условиям:
- не более 500 мм;
-
не более
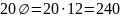 мм,
как для сварных каркасов не более
меньшего размера сечения колонны 400 мм.
мм,
как для сварных каркасов не более
меньшего размера сечения колонны 400 мм.