Кривая Кох.

Пример предложен Хельгой фон Кох в 1904 г. Построение, представленное на рис. П.1, начинается (n=0) с отрезка прямой длиной L(1)=1. Отрезок делится на три части, средняя часть вынимается, вместо нее встраиваются две стороны равностороннего треугольника, длиной 1/3 каждая. В результате получаем кривую первого поколения (n=1) из четырех прямолинейных звеньев, каждое длиной по 1/3. Длина кривой первого поколения составляет величину L(1/3)=4/3. Следующее поколение получается при замене каждого прямолинейного звена уменьшенным образующим элементом. В результате получим кривую второго поколения (n=2), состоящую из N=4²=16 звеньев. Каждое звено имеет длину δ=3^-2=1/9. Длина кривой второго поколения равна L(1/9)=(4/3)²=16/9. Заменяя все звенья предыдущего поколения кривой уменьшенным образующим элементом (треугольником без нижней стороны ), получаем новое поколение кривой. Кривые для трех поколений представлены на рис. П.1. Кривая n-ного поколения при любом конечном n называется предфракталом.

Рис. П. 1. Кривая Кох.

Первые четыре шага построения.

Получим выражение для величины размерности D. Длина предфрактала зависит от номера поколения и для n-го поколения определяется формулой

Длина каждого звена составляет δ=3^-n. Отсюда число поколений n можно представить в виде

n = -ln δ /ln3.

Длина предфрактала запишется в виде

(П.2)

Сравнивая формулу (П.2) с формулой (П.1), получим выражение для фрактальной размерности кривой Кох:

D = ln 4/ln 3 ~ 1,2628.

На каждой стадии построения предфракталы Кох могут быть растянуты в линию, поэтому топологическая размерность триадной кривой Кох D_τ=1. Таким образом, кривая Кох – фрактальное множество с фрактальной размерностью D=ln 4/ln 3.

Сходным образом строятся фрактальные треугольная салфетка и ковер Серпинского, изображенные на рис. П2, П3.

Рис. П. 2. Построение треугольной салфетки Серпинского. Начальный элемент – треугольник со всеми внутренними точками. Образующий элемент исключает из него центральный треугольник. На рисунке показаны пять поколений предфракталов. Фрактальное множество получается в пределе при бесконечно большом числе поколений и имеет фрактальную размерность D=ln3/ln2=1,58…

Рис. П. 3. Построение ковра Серпинского. Начальный элемент – черный квадрат со стороной, равной 1. Из него вырезается белый квадрат, со стороной, равной 1/3. Далее из каждого черного квадрата вырезается снова белый квадрат, со стороной, равной 1/3 стороны черного квадрата. На рисунке показаны четыре поколения предфракталов. Размерность подобия D=ln8/ln3=1,89…

Канторово множество

Канторово множество названо в честь великого математика Георга Кантора (1845-1918), открывшего его в 1883 г. Построение кривой Кох можно рассматривать как процесс добавления к отрезку все более мелких деталей. Построение канторова множества сводится к выбрасыванию из первоначального отрезка все более мелких отрезков (рис. П5).

Рис. П.  4. Канторово множество

Построение начинается с отрезка длины 1, который делится на 3 равные части. Затем средняя часть изымается. Число отрезков станет 2, а их полная длина уменьшится до 2/3. Затем процесс повторяется на каждом из оставшихся отрезков. На каждом этапе отбрасывание средней трети удваивает число отрезков и уменьшает общую длину на одну треть. В пределе полная длина канторова множества стремится к нулю, а его фрактальная размерность, которую можно вычислить по аналогии с формулой (П.2), составит

D = ln2/ln3 ~ 0,63092. (П.3)

Реальные системы, имеющие фрактальную структуру, имеют конечную массу. Пример распределения массы в фрактальном множестве дает канторов стержень. Будем считать первоначальным элементом не единичный отрезок, а стержень из какого-либо материала с плотностью ρ₀. Исходный стержень имеет длину l₀=1, и, следовательно, массу, μ₀ =1.

Разрезаем стержень на две половины равной массы μ₁ = μ₂ = 0,5, которые затем в результате ковки укорачивают до длины l₁ =1,3. (одинаковой для обеих половин). В результате такой обработки плотность возрастает до ρ₀ = μ₁/l₁ = 3/2. Повторяя процедуру, получим в n-м поколении N=2ⁿ стержней, каждый из которых имеет длину l_i =3^-n и массу μ_i =2^-n при i = 1,…, N – номер стержня. При этом общая масса в ходе обработки сохраняется, поэтому

Мандельброт сравнивает этот процесс со свертыванием молока, когда первоначально равномерное распределение массы в результате разбивается на множество мелких областей с высокой плотностью. На рис. П.5 изображен вариант триадного канторова стержня.

Рис. П. 5. Триадный канторовский стержень. Высота стержня

в n-м поколении пропорциональна его плотности

На основе канторова стержня можно получить интересную конструкцию, называемую «чертова лестница». Выбрав за начало отсчета левый конец стержня, запишем массу, содержащуюся на отрезке [0,x] в виде:

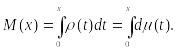
Здесь плотность ρ(x) равна нулю в промежутках и равна бесконечности во всех бесконечно многих точках, образующих канторово множество. Масса М(х) остается постоянной на интервалах, соответствующих пустым промежуткам. Длины таких интервалов в сумме равны 1, то есть длине исходного стержня. Для обычной (не фрактальной) гладкой кривой отсюда можно было бы сделать заключение, что М(х)=0. Но масса возрастает бесконечно малыми скачками в точках канторова множества, и эти скачки в сумме дают М(1)=1. Зависимость массы от х, изображенная на рис. П.6., напоминает лестницу, которая почти всюду горизонтальна. Самоподобие этой лестницы видно из рисунка. Сходное распределение массы характерно для большинства объектов фрактальной структуры.

Рис. П. 6. Масса канторова стержня как функция координаты.

Объект называется чертовой лестницей (devil’s staircase)