3.1. Результаты расчётов

Расчёт задачи исследования с исходными данными при помощи Excel представлен на рисунке 8.

Рисунок 8 - Расчёт задачи исследования

Из полученных значений мы видим, что 35% из числа поступивших заявок не принимаются к обслуживанию (0,352). Так же только 65% из числа поступивших заявок будут обслужены, тогда как приемлемый уровень обслуживания должен быть выше 90%.

1. Изменение параметров

Исследуем зависимость критериев эффективности от числа n при помощи Excel (рисунок 9):

Рисунок 9 - Расчёт значений СМО при разных n

Проиллюстрируем зависимость параметра от n на графике (рисунок 10).

Рисунок 10 - Зависимость параметра от n

Как видно из графика, увеличение числа каналов положительно влияет на величину вероятности отказа – она убывает.

Далее исследуем зависимость критериев эффективности от среднего времени обслуживания.

При = 2,5 мин/зв (рисунок 11):

Рисунок 11 - Расчёт значений СМО при = 2,5 мин/зв.

Уменьшение среднего времени обслуживания на 0,5 минуты не уменьшило вероятность отказа до допустимого значения ( 0,289).

При = 2 мин/зв (рисунок 12):

Рисунок 12 - Расчёт значений СМО при = 2 мин/зв.

Вероятность отказа по-прежнему большая ( 0,211).

При = 1,5 мин/зв (рисунок 13):

Рисунок 13 - Расчёт значений СМО при = 1,5 мин/зв.

Вероятность отказа уже близка к допустимым границам (0,133)

При = 1,2 мин/зв (рисунок 14):

Рисунок 14 - Расчёт значений СМО при = 1,2 мин/зв.

Вероятность отказа меньше 10% ( 0, 084) — это означает, что при = 1,2 и меньше, система будет работать эффективно. Проверим это при = 1 мин/зв (рисунок 15):

Рисунок 15 - Расчёт значений СМО при = 1 мин/зв.

Действительно, вероятность отказа уменьшилась ещё больше (.

Проиллюстрируем зависимость параметра от на графике (рисунок 16).

Рисунок 16 - Зависимость параметра от

На графике наглядно видно, что чем меньше среднее время обслуживания заявки, тем меньше вероятность отказа, что и было.

В последнем численном эксперименте совместим изменение числа каналов и среднего времени обслуживания, чтобы найти наиболее оптимальное решение.

Анализируя полученные ранее значения можно предположить, что при n=5 и = 2 мин/зв. Вероятность отказа примет допустимое значение. Проверим это (рисунок 17):

Рисунок 17 - Расчёт значений СМО при n = 5 и = 2 мин/зв.

Действительно, данная комбинация приводит к эффективному результату ( = 0,1).

3.2. Выводы по проделанной работе

При проведении численных экспериментов с ключевыми параметрами СМО, которые в наибольшей степени влияют на критерий эффективности были сформированы следующие выводы:

1. Увеличение числа каналов положительно влияет на величину вероятности отказа – она убывает. Оптимальным числом каналов для оптимизации задачи исследование является n=7, при котором 0,068

2. Уменьшение среднего времени обслуживания заявки приводит к уменьшению вероятности отказа. Оптимальным средним временем обслуживания является 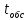= 1,2 мин/зв при котором = 0,084.

Но так как увеличение числа операторов до 7 может являться финансово невыгодной процедурой, а уменьшение среднего времени обслуживания до 1, 2 мин/зв практически невозможно (а если возможно, то только с проведением технической модернизации процесса обслуживания, что также является экономически невыгодной операцией), было найдено оптимальное решение, при котором финансовые затраты не так велики, а результат имеет ярко выраженный эффективный характер.

При увеличении числа каналов обслуживания до 5 и уменьшении среднего времени обслуживания до 2 мин/зв вероятность отказа принимает допустимое значение 0,1. Достижение данных показателей возможно при принятии на работу ещё одного оператора и проведении, к примеру, курсов по повышению эффективности обслуживания, что позволит без привлечения дорогостоящих технических устройств и программных продуктов уменьшить среднее время обслуживания до 2 мин/зв.

ЗАКЛЮЧЕНИЕ

В ходе проделанной работы была изучена общая теория систем массового обслуживания и, в частности, СМО с отказами. Был рассмотрен способ моделирования СМО с помощью табличного процессора Excel и на его основе произведена разработка расчётного инструментария для решения задачи исследования.

Правильность составления листа была проверена с помощью онлайн-сервиса. По результатам проверки значительных расхождений в полученных значениях обнаружено не было.

При решении задачи исследования было выявлено, что система работает не эффективно, что обусловлено большим процентом вероятности отказа из чего был сделан вывод о необходимости оптимизации.

В результате экспериментов со значениями показателей, влияющих на вероятность отказа в обслуживании, было найдено оптимальное решение и даны рекомендации для оптимизации

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Мицель А.А., Грибанова Е.Б., Имитационное моделирование экономических процессов в Excel Томск: Изд-во ТУСУР, 2016. – 115 с

2. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. – М.: КомКнига, 2005.

3. Вентцель Е.С. Исследование операций: Задачи, принципы, методология. Учебное пособие – М.: Дрофа, 2004.

4. Ивницкий В.А. Теория сетей массового обслуживания. – М.: Физматлит, 2004.

5. Таха Х.А. Введение в исследование операций. – М.: ВИЛЬЯМС, 2007.

6. Таха Х.А. Теория вероятностей и математическая статистика – М.: Издательский дом «Вильямс», 2001.

7. Якимов И.М., Кирпичников А.П., Зайнуллина Г.Р. и др. Информационная система имитационного и аналитического моделирования систем массового обслуживания // Вестник Технологического университета. 2016. № 5. С. 141–145

8. Ивченко, Г.И. Теория массового обслуживания/ Г.И.Ивченко, В.А.Каштанов, И.Н.Коваленко. М., 1982

9. Кениг, Д. Методы теории массового обслуживания /Д.Кениг, Д.Штойян.: Пер. с нем. /Под. ред. Г.П.Климова. М., 1981.

10. Саати, Т.Л. Элементы теории массового обслуживания и ее приложения / Т.Л Саати/: Пер. с англ. /Под. ред. И.Н. Коваленко, изд-ие 2. М., 1971.

11. Мат. Семестр [электронный ресурс] – Режим доступа: https://math.semestr.ru, свободный. – Загл. с экрана. (Дата обращения: 12.12.2018).