СОДЕРЖАНИЕ

ВВЕДЕНИЕ 3

1.Постановка задач массового обслуживания 5

1.1. Общие сведения о СМО 5

1.2. Моделирование СМО в табличном процессоре Excel 11

1.3. Постановка задачи 13

2. Выполнение расчётов 14

2.1. Разработка расчётного инструментария 14

2.2. Расчёт контрольного примера 15

3. Состав проводимых численных экспериментов 20

3.1. Результаты расчётов 20

3.2. Изменение параметров 24

3.3. Выводы по проделанной работе 25

ЗАКЛЮЧЕНИЕ 27

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 28

ВВЕДЕНИЕ

Возникновение теории массового обслуживания относится к началу XX в. и связано с необходимостью решения задач строительства и развития телефонных сетей. Большой вклад в развитие и становления теории массового обслуживания внесли зарубежные ученые Ф.В. Иоханнсен, А. К. Эрланг, а также отечественный математик А.Я. Хинчин, систематизировавший достигнутые к тому времени основные положения теории массового обслуживания в монографии «Работы по теории массового обслуживания» (1963) [2]. В зарубежной практике указанное направление исследований известно под названием «Теории очередей».

Теорию массового обслуживания следует рассматривать как раздел прикладной математики, изучающий процессы, связанные с удовлетворением массового спроса на выполнение какого-либо вида услуг с учетом случайного характера спроса и обслуживания.

Задача теории массового обслуживания – установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных показателей (количества каналов в системе, параметров входящего потока заявок и т.д.). Результирующими показателями или интересующими нас характерисуноктиками СМО являются – показатели эффективности СМО, которые описывают способна ли данная система справляться с потоком заявок.

Задачи теории массового обслуживания носят оптимизационный характер и в конечном итоге включают экономический аспект по определению такого варианта системы, при котором будет обеспечен минимум суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на обслуживание и простоев каналов обслуживания.

В качестве примеров СМО в финансово-экономической сфере можно привести системы, представляющие собой банки различных типов (коммерческие, инвестиционные, ипотечные, инновационные, сберегательные), страховые организации (государственные, акционерные общества, компании, фирмы, ассоциации, кооперативы), налоговые инспекции, аудиторские службы, различные системы связи (в том числе телефонные станции), погрузочно-разгрузочные комплексы (порты, товарные станции), автозаправочные станции, различные предприятия и организации сферы обслуживания (магазины, парикмахерские, больницы).

1. Постановка задач массового обслуживания

1. Общие сведения о смо

Каждая система массового обслуживания (СМО) может быть представлена в виде определенного числа обслуживающих единиц, которые называются каналами обслуживания. В качестве канала могут рассматриваться различного вида приборы и приспособления, вычислительная машина, коллектив людей или отдельный исполнитель, выполняющий определенный вид работ. По числу каналов СМО делится на одноканальные и многоканальные системы.

Функционирование любой СМО заключается в обслуживании поступающего в нее потока заявок или требований. Заявки обычно поступают нерегулярно, образуя случайный поток заявок (требований). На обслуживание заявки также необходимо определенное время. Случайный характер потока заявок и времени обслуживания приводит к неравномерной загрузке СМО. В какие-то периоды времени скапливается большое количество заявок (они либо становятся в очередь, либо покидают СМО, не получив обслуживания), в другие периоды СМО может работать с недогрузкой или простаивать [9].

Систематизируем основные термины и понятия, используемые в теории массового обслуживания.

Системой массового обслуживания называется любая система, предназначенная для обслуживания каких-либо заявок (требований), поступающих в нее в случайные моменты времени [7].

Под обслуживанием понимается удовлетворение потребности в чем-то. По своей природе обслуживание может иметь самый различный характер.

Основными элементами СМО являются входной поток заявок, очередь (может отсутствовать), каналы обслуживания и выходящий поток. Обобщенная структурная схема СМО показана на рисунке 1:

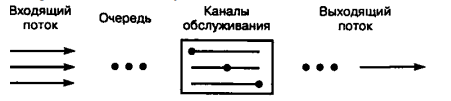
Рисунок 1 - Обобщенная структурная схема СМО

В зависимости от формирования СМО, ее различают на:

1. Системы с отказами, в которых при занятости, заявка не встает в очередь и при это она покидает систему обслуживания.

2. Системы с неограниченными ожиданиями, в которых заявка встает в очередь, если в момент поступления все каналы были заняты.

Существуют и системы смешанного типа с ожиданием ограниченной длиной очереди, это когда заявка получает отказ, если приходит в момент, когда все места в очереди заняты. Заявка, попавшая в очередь, обязательно обслуживается [1].

По числу каналов обслуживания СМО делятся на одноканальные и многоканальные.

В зависимости от расположения источника требований системы могут быть разомкнутыми, (источник заявок находится вне системы) и замкнутыми (источник находится в самой системе) [5].

Характеристики СМО

Заявки характеризуются:

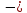• интенсивность потока заявок (число заявок в единицу времени);

• вероятность отказа в обслуживании (доля не обслуженных заявок). Очередь характеризуется:

• m – длина очереди;

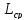• – средняя длина очереди;

• – среднее время ожидания в очереди;

• – вероятность попадания в очередь (доля заявок, попавших в очередь). Каналы обслуживания характеризуются;

• n – число каналов обслуживания;

• – среднее время обслуживания одной заявки;

• – интенсивность обслуживания (число обслуженных заявок в единицу времени);   ;

• среднее число занятых каналов; ;

• – среднее число свободных каналов;

• коэффициент загрузки канала;

• – вероятность обслуживания (доля обслуженных заявок);

• интенсивность нагрузки; ρ  ;

• – среднее время простоя каналов;

• – среднее время пребывания заявки в СМО;

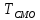• – среднее число заявок в СМО.

Параметры структуры СМО

Каждая система массового обслуживания обладает определенной структурой, характеризующейся совокупностью параметров [3]. Основным компонентом структуры СМО являются каналы обслуживания. В зависимости от числа каналов различают одноканальные и многоканальные СМО.

Дисциплина очереди

Дисциплина очереди определяет принцип, в соответствии с которым поступающие на вход обслуживающей системы требования подключаются из очереди к процедуре обслуживания [8].

Наиболее распространенный принцип ее построения основан на правиле

«первым пришел – первым обсуживаешься» (часто обозначается аббревиатурой FIFO – от английского First-In-First-Out). Второе правило (например, при обработке документов) – «последним пришел – первым обслуживаешься» (обозначается аббревиатурой LIFO – от англ. Last-In-First-Out) [10]. Могут использоваться случайный отбор заявок, учет определенных приоритетов, вводиться ограничение на время пребывания заявки в очереди.

Входящий поток

Входящий поток наиболее распространен в практике это простейший поток заявок, обладающий свойствами стационарности, ординарности и отсутствия последствия.

1. Свойством стационарности, которое выражает неизменность вероятностного режима потока по времени. Это значит, что число требований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным. Например, число вагонов, поступающих под погрузку в среднем в сутки должно быть одинаковым для различных периодов времени [6].

2. Отсутствие последствия, которое обслуживает взаимную независимость поступления того или иного числа требований на обслуживание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от числа требований, обслуженных в предыдущем промежутке времени.

3. Свойством ординарности, которое выражает практическую невозможность одновременного поступления двух или более требований (вероятность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю).

Входящий поток требований представляет собой совокупность требований, которые поступают в систему и нуждаются в обслуживании. Входящий поток требований изучается с целью установления закономерностей этого потока и дальнейшего улучшения качества обслуживания [4].

В большинстве случаев входящий поток неуправляем и зависит от ряда случайных факторов. Число требований, поступающих в единицу времени, случайная величина. Случайной величиной является также интервал времени между соседними поступающими требованиями. Однако среднее количество требований, поступивших в единицу времени, и средний интервал времени между соседними поступающими требованиями предполагаются заданными.

Среднее число требований, поступающих в систему обслуживания за единицу времени, называется интенсивностью поступления требований.

На практике условия простейшего потока не всегда строго выполняются. Часто имеет место не стационарность процесса (в различные часы дня и различные дни месяца поток требований может меняться, он может быть интенсивнее утром или в последние дни месяца) [7]. Существует также наличие последствия, когда количество требований на отпуск товаров в конце месяца зависит от их удовлетворения в начале месяца.

Простейшей одноканальной моделью с вероятностным входным потоком и процедурой обслуживания является модель, характеризуемая показательным распределением как длительностей интервалов между поступлениями требований, так и длительностей обслуживания. При этом плотность распределения длительностей интервалов между поступлениями требований имеет вид:

,

где  - интенсивность поступления заявок в систему.

Под интенсивностью потока понимают:

,

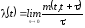где m(t, t+) - среднее число событий в интервале (t, t+).

Плотность распределения длительностей обслуживания:

,

где  - интенсивность обслуживания.

Выходящий поток

Совокупность обслуженных и потерянных заявок образует выходящий поток СМО.

В зависимости от структуры выходящего потока различают СМО без потерь и СМО с потерями. Для СМО без потерь характерно отсутствие ограничений на число мест в очереди и на время пребывания заявки в системе. По этой причине выходящий поток будет состоять лишь из обслуженных заявок.

В свою очередь, поток потерянных заявок может состоять из потока заявок, получивших отказ, и потока не «терпеливых» заявок, покинувших систему, так как их время пребывания превысило допустимую величину.

Выходящий поток в общем случае распадается на поток обслуженных и поток потерянных заявок.

Выходящий поток заявок связан с потоком обслуживания в канале, где длительность обслуживания t_обс является случайной величиной и подчиняется закону распределения с плотностью:

где μ – интенсивность потока обслуживания, т.е. среднее число заявок, обслуживаемых в единицу времени:

(чел./мин, р./ дн., кг/ч, докум./дн.),

где 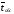- среднее время обслуживания.

Важной характеристикой СМО, объединяющей λ и μ, является интенсивность нагрузки:

.

СМО с отказами

Заявка, поступившая в систему с отказами, при этом все каналы заняты, получает отказ и покидает систему необслуженной. Показателем качества обслуживания выступает вероятность получения отказа. Предполагается, что все каналы доступны в равной степени всем заявкам, входящий поток является простейшим, длительность (время) обслуживания одной заявки распределена по показательному закону [2].

По ниже написанным формулам можно рассчитать СМО с отказами:

1. Вероятность простоя каналов обслуживания, когда нет заявок (k = 0):

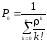
2. Вероятность отказа в обслуживании, когда поступившая на обслуживание заявка найдет все каналы занятыми (k = n):

;

3. Вероятность обслуживания:

;

4. Среднее число занятых обслуживанием каналов:

;

5. Доля каналов, занятых обслуживанием:

;

6. Абсолютная пропускная способность СМО:

;

1.2. Моделирование с помощью табличного процессора Excel

Имитация с помощью табличных процессоров (spreadsheet simulation) представляет собой отдельное направление со своими особенностями. Его сторонники утверждают, что использование данных систем улучшает понимание происходящих процессов гораздо лучше, чем применение специализированного программного обеспечения, имеющего высокую стоимость и требующего время для изучения, а также скрывающего используемые механизмы (хотя такие среды довольно широко используются, особенно GPSS, поскольку предоставляют больше возможностей и позволяют моделировать сложные системы) [1].

Так, Grossman в своей публикации «Spreadsheet Modeling and Simulation Improves Understanding of Queues» утверждал, что имитация с помощью таблиц Excel гораздо лучше дает представление о системах массового обслуживания, чем теория очередей, и также развивает интуицию, дает даже незнакомым с программированием специалистам опыт реализации различных моделей [1]. Однако эти подходы (реализация с помощью Excel и сред моделирования) не являются взаимоисключающими, а скорее дополняют друг друга.

В том случае, если обслуживание заявок может происходить в нескольких узлах, то говорят, что данная система является многоканальной. Рассмотрим двухканальную СМО. Предположим, что вновь поступившая заявка поступает в тот канал, который раньше других освободился (а при одновременном освобождении заявка поступит в первый узел), тогда процесс моделирования можно представить следующим образом (рисунок 2) (исходные данные: tz =8 мин., to =7 мин.; t0 =9 ч.).

Рисунок 2 - Двухканальная СМО

Для каждого канала выполняется расчет времени начала и окончания обслуживания. Решение о том, в каком канале будет происходить обслуживание, принимается на основе данных о времени освобождения каждого из них. Время начала обслуживания заявки равно максимальному значению из следующих величин: время освобождения найденного канала и время прибытия заявки

Е8=ЕСЛИ(МАКС(F$7:F7)<=МАКС(H$7:H7);МАКС(F$7:F7;C8);"")

F8=ЕСЛИ(ЕТЕКСТ(E8);"";E8+D8)

G8=ЕСЛИ(МАКС(F$7:F7)>МАКС(H$7:H7);МАКС(H$7:H7;C8);"")

H8=ЕСЛИ(ЕТЕКСТ(G8);"";G8+D8).

Время ожидания обслуживания определяется по формуле I8=ЕСЛИ(ЕТЕКСТ(E8);G8-C8;E8-C8) (рисунок 3).

Рисунок 3 - Моделирование СМО в Excel