4.4.2. Практические приложения метода Монте – Карло

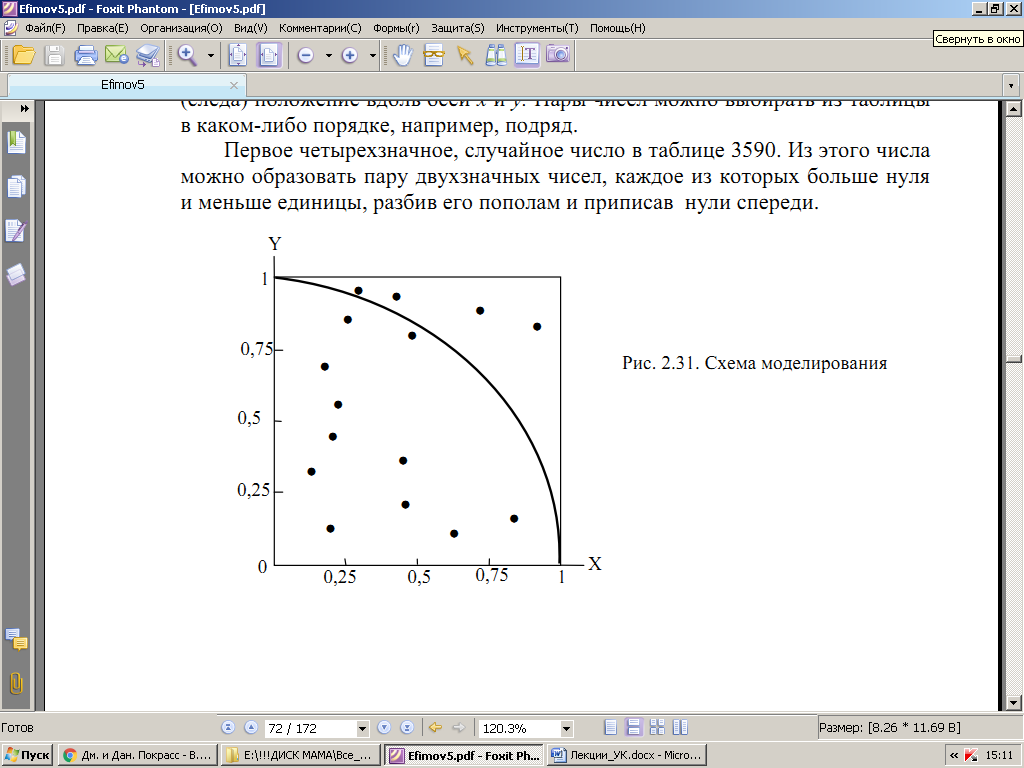
Решим задачу о вычислении площади круга методом Монте–Карло. Нарисуем квадрат, сторону которого примем за единицу длины. Впишем в этот квадрат четверть круга (рис. 4.14). Если такой чертеж некоторое время подержать под дождем, то на его поверхности останутся следы капель. Подсчитаем число следов внутри квадрата и внутри круга (сектора). Очевидно, что их отношение будет равно отношению площадей этих двух фигур, так как попадание капель в различные места чертежа равновероятно.

Теперь заменим дождь таблицей случайных чисел (табл.4.8). Каждому следу капли можно сопоставить два случайных числа, характеризующих его (следа) положение вдоль осей х и у. Рис. 4.14. Схема моделирования

Пары чисел можно выбирать из таблицы в каком-либо порядке, например, подряд.

Таблица 4.8. Таблица случайных чисел

Первое четырехзначное, случайное число в таблице 3590. Из этого числа можно образовать пару двухзначных чисел, каждое из которых больше нуля и меньше единицы, разбив его пополам и приписав нули спереди.

Первое из них пусть будет абсциссой следа капли, второе – ординатой. Таким образом, координаты первого следа капли: х = 0,35 и у = 0,90. Аналогично поступаем со всеми остальными случайными числами в таблице. Координаты пятнадцати капель, соответствующих первому столбцу случайных чисел, запишем в табл.4.9.

Таблица 4.9

На рис. 4.14 нанесены случайные точки, отвечающие этим координатам – внутрь круга попало 11 капель, за пределы круга (но внутри квадрата) – 4 капли. Попробуем грубо оценить площадь четверти круга: она будет равна отношению числа точек, лежащих внутри него, к полному числу точек, т. е. 11/15 = 0,73.

Расчетное значение площади части круга равно π/4, т. е. 0,79. Таким образом, даже при использовании всего 15 точек можно достаточно точно определить площадь круга. Ошибка составляет 8%.

Эту же задачу можно использовать для статистической оценки числа π. Получим π = 0,73·4 = 2,9. Ошибка составляет 10%.

Если увеличить число точек дождя, то точность расчетов значительно возрастет в соответствии с законом больших чисел.

В настоящем примере использована часть круга определенного радиуса. Но приведенный выше метод статистического моделирования можно использовать при любой геометрии кривой. При этом, чем более искаженной (от окружной) будет линия, тем больше потребуется опытов. Аналогичным образом можно вычислять площадь любой другой фигуры.

Для вычисления объемов пространственных тел нам нужна уже третья точка – ось z, перпендикулярная плоскости ху. Очевидно, что определение объемов трехмерного тела можно проводить тем же способом, что и вычисление площади. Поместим интересующее нас тело в куб и заполним его объем равномерно распределенными случайными числами. Отношение объема тела к объему куба определяется отношением числа точек, находящихся в теле, к полному числу точек. Положение точки характеризуется тремя координатами, поэтому каждой точке нужно сопоставить тройку случайных чисел. Таким образом, можно вычислять не только объемы и площади, но и другие характеристики двухмерных и трехмерных тел, например массу и положение центра тяжести тела по заданному распределению плотности в его объеме.

Ряд задач квантовой физики, теории элементарных частиц, теории вероятности, статистической физики часто могут быть решены после вычисления многомерных пространств.