3.2.2. Определение уравнений регрессии

Корреляционную зависимость между переменными X и Y можно выразить с помощью уравнений типа

которые называются уравнениями регрессии. В этих уравнениях и являются средними арифметическими переменных X и Y.

Графическое выражение регрессионного уравнения называют линией регрессии. Линия регрессии выражает наилучшее предсказание зависимой переменной Y по независимым переменным X (рис. 3.3). Эти независимые переменные в математике называются предикатами.

Корреляционную зависимость можно выразить с помощью двух уравнений регрессии, которые в самом простом случае выглядят как уравнения прямой: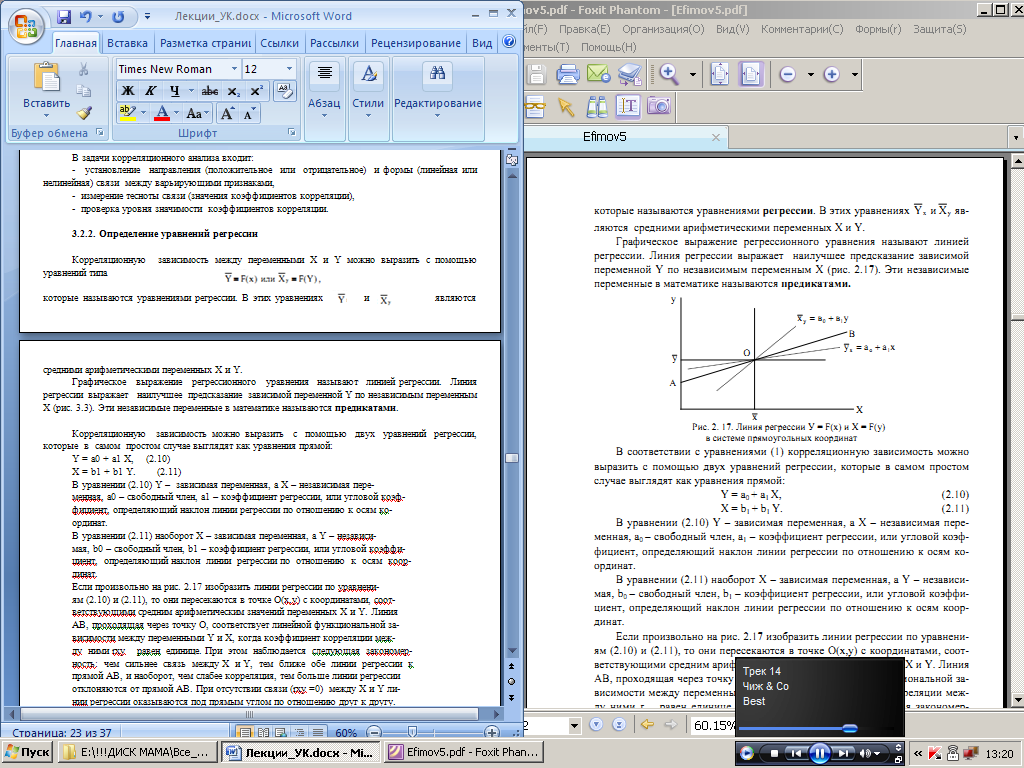

Y = a₀ + a₁ X, (3.1)

X = b₀ + b₁ Y. (3.2)

В уравнении (3.1) Y – зависимая переменная, а X – независимая переменная, a₀ – свободный член, a₁ – коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат.

Рис. 3.3. Линия регрессии У = F(x) и X = F(у) в системе прямоугольных координат

В уравнении (3.2) наоборот X – зависимая переменная, а Y – независимая, b₀ – свободный член, b₁ – коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат.

Если произвольно на рис. 3.37 изобразить линии регрессии по уравнениям (3.1) и (3.2), то они пересекаются в точке O(x,y) с координатами, соответствующими средним арифметическим значений переменных X и Y. Линия AB, проходящая через точку O, соответствует линейной функциональной зависимости между переменными Y и X, когда коэффициент корреляции между ними r_xy равен единице. При этом наблюдается следующая закономерность: чем сильнее связь между X и Y, тем ближе обе линии регрессии к прямой АВ, и наоборот, чем слабее корреляция, тем больше линии регрессии отклоняются от прямой АВ. При отсутствии связи (r_xy =0) между X и Y линии регрессии оказываются под прямым углом по отношению друг к другу.

Количественное установление связи (зависимости) между X и Y (или между Y и X) называется регрессионным анализом. Главная задача регрессионного анализа состоит:

- в определение коэффициентов a₀, b₀, a₁, b₁,

- в определение уровня значимости полученных уравнений регрессии (3.1) и (3.2), связывающих между собой переменные X и Y.

Если до проведения регрессионного анализа выполнен корреляционный анализ переменных и определены коэффициенты корреляции между ними, то легко определить коэффициенты регрессии a₁ и b₁ по формулам:

где Sx, Sy – среднеквадратические отклонения, подсчитанные для переменных X и Y соответственно.

Можно рассчитать коэффициенты регрессии и без подсчета среднеквадратических отклонений по формулам:

(3.3)

В том случае, если коэффициент корреляции неизвестен, коэффициенты регрессии можно вычислить по следующим формулам:

(3.4)

Зная коэффициенты регрессии, можно легко получить коэффициент корреляции:

(3.5)

Свободные члены уравнений регрессии a₀ и b₀ вычисляются по следующим формулам:

(3.6)

Трудоемкость вычислений по формулам (3.4),(3.5),(3.6) свободных членов и коэффициентов регрессии достаточно велика, поэтому в регрессионном анализе используются более простые методы их определения, базирующиеся на методе наименьших квадратов.

Применяя этот метод для линейной функции зависимости переменных, получим две системы уравнений, позволяющие определить из одной системы величины a₀ и a₁:

(3.7)

а из другой системы величины b₀ и b₁:

(3.8)

где N – число переменных x или y.

Приведем пример вычисления коэффициентов линейной регрессии.

Допустим, что при исследовании статистической зависимости между объемом снятого в процессе токарной обработки материала заготовки Q и глубиной резания s получены следующие результаты эксперимента (табл. 3.4):

Графическое отражение экспериментальных данных приведено на рис.3.4.

Таблица 3.4

Уравнение регрессии при этом имеет вид

Y = a₀ + a₁·X,

где в качестве независимой переменной X выступает глубина резания s, а в качестве зависимой переменной Y выступает объем снятого материала Q.

Для решения уравнений (3.7) заполним вспомогательную таблицу 3.5.

Подставляя значения данных табл.3.5 в уравнение (3.7), получим следующую систему линейных уравнений:

a₀ ·12 + a₁·39,60 = 51,43, a₀⋅39,60 + a₁·136,40 = 177,28.

Решая эту систему уравнений, получим a₀ = -0,06 ; a₁= 1,28.Тогда Y = -0,06+ 1,28·X.

Для решения уравнения регрессии X = b₀ + b₁·Y получим следующую систему уравнений:

b₀·12 + b₁·51,43 = 39,60, b₀ ·51,43 + b₁·230,52 = 177,28.

Решая эту систему уравнений, получим b₀ = 0,08; b₁ = 0,75. Тогда X = 0,08 + 0,75·Y.

Таблица 3.5

Рис. 3.4. Экспериментальная зависимость сошлифованного материала Q от глубины резания s; а – линия регрессии Q = f (s)